Description du projet
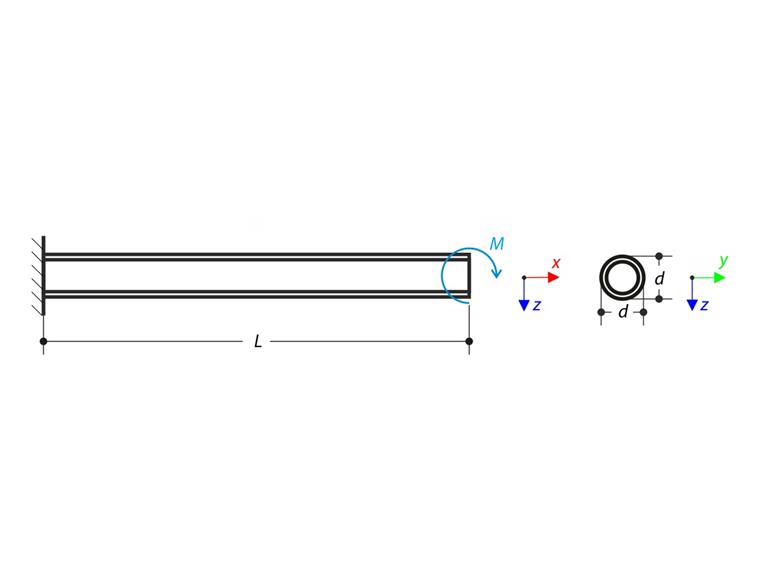
Un porte-à-faux est chargé par le moment M à son extrémité libre. Déterminez les flèches maximales ux et uz à l'extrémité libre à l'aide de la théorie du premier ordre, de l'analyse des grandes déformations et en négligeant le poids propre de la poutre '. L'exemple de vérification est basé sur l'exemple introduit par Gensichen et Lumpe (voir la référence).
| Matériau | Acier | Module d'élasticité | E | 210000,000 | MPa |
| Module de cisaillement | G | 81000,000 | MPa | ||
| Géométrie | Porte-à-faux tubulaire | Périmètre | L | 4,000 | m |
| Diamètre | d | 42,400 | mm | ||
| Épaisseur de voile | t | 4,000 | mm | ||
| Import | Moment fléchissant | M | 3,400 | kNm |
Solution analytique
Analyse géométriquement linéaire
En considérant la théorie du premier ordre, le problème peut être résolu grâce à l’équation d’Euler-Bernoulli. Pour la géométrie, les charges et les conditions aux limites données, la flèche maximale résultante uz,max est la suivante:
La flèche ux, max en considérant l'analyse géométriquement linéaire est nulle.
analyse des grandes déformations
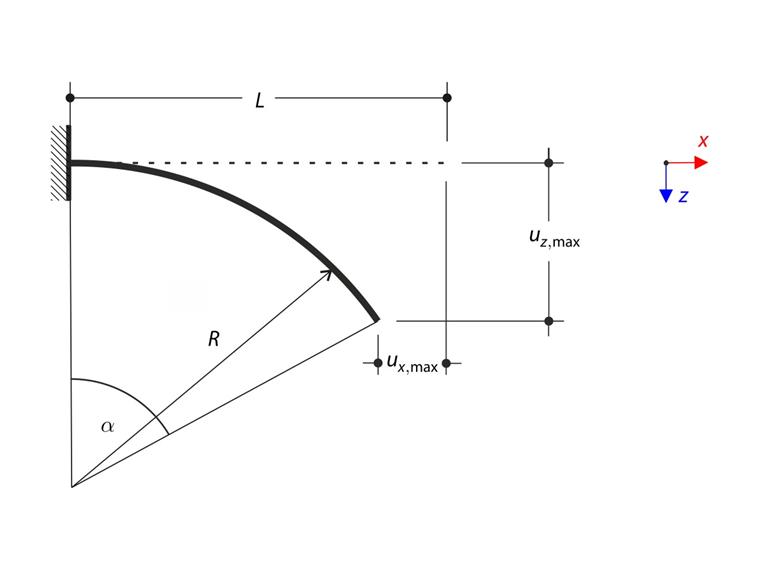
Dans l'analyse des grandes déformations, une poutre est décrite par une équation différentielle non linéaire et illustrée dans la figure suivante.
Le terme du côté droit est constant et par conséquent le côté gauche, qui est directement la courbure de la poutre κ, est également constant. La seule courbe à courbure constante est un cercle, la solution à ce problème consiste donc à utiliser un arc de cercle de rayon R.
R = rayon de l'arc. L'angle de l'arc de cercle α est égal à α=L/R.
Paramètres de RFEM et RSTAB
- Modélisé dans RFEM 5.05, RSTAB 8.05 et RFEM 6.01, RSTAB 9.01
- La taille de l'élément est lEF = 0,400 m
- Le nombre d'incréments est de 5
- Le modèle de matériau isotrope linéaire élastique est utilisé
- La rigidité de cisaillement des barres est activée
- La division de barre pour l'analyse des grandes déformations ou post-critique est activée
résultats
| ux, max [m] | Solution analytique | RFEM6 | Ratio | RSTAB 9 | Ratio |
| Analyse géométriquement linéaire | 0,000 | 0,000 | - | 0,000 | - |
| analyse des grandes déformations | -0,337 | -0,336 | 0,997 | -0,336 | 0,997 |
| uz, max [m] | Solution analytique | RFEM6 | Ratio | RSTAB 9 | Ratio |
| Analyse géométriquement linéaire | 1,441 | 1,441 | 1,000 | 1,441 | 1,000 |
| analyse des grandes déformations | 1,379 | 1,380 | 1,001 | 1,380 | 1,001 |
| ux, max [m] | Solution analytique | RFEM5 | Ratio | RSTAB 8 | Ratio |
| Analyse géométriquement linéaire | 0,000 | 0,000 | - | 0,000 | - |
| analyse des grandes déformations | -0,337 | -0,338 | 1,003 | -0,337 | 1,000 |
| uz, max [m] | Solution analytique | RFEM5 | Ratio | RSTAB 8 | Ratio |
| Analyse géométriquement linéaire | 1,441 | 1,441 | 1,000 | 1,441 | 1,000 |
| analyse des grandes déformations | 1,379 | 1,380 | 1,001 | 1,380 | 1,001 |
,_LC1__LI.jpg?mw=760&hash=8a72fd14929115d349aeafc6a154c475e761a1ac)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
