Descrizione
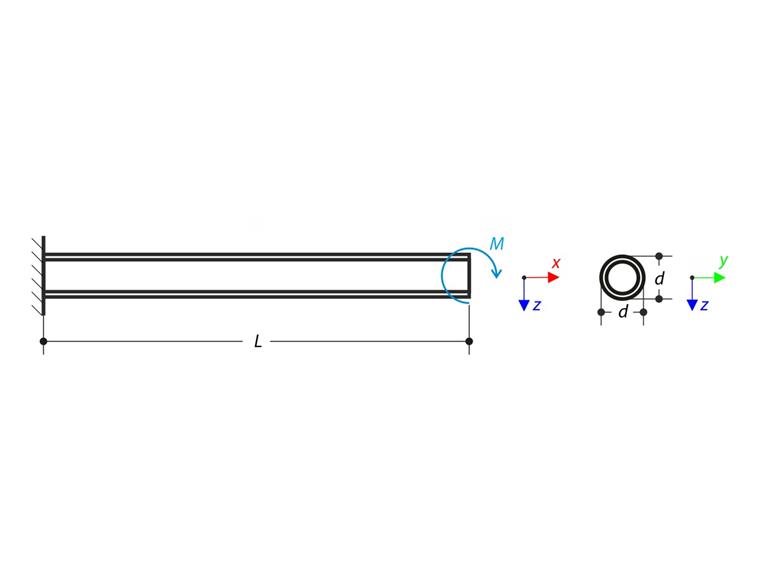
Uno sbalzo è caricato dal momento M alla sua estremità libera. Utilizzando l'analisi geometricamente lineare e l'analisi a grandi spostamenti e trascurando il peso proprio della trave's, determinare le inflessioni massime ux e uz all'estremità libera. L'esempio di verifica si basa sull'esempio introdotto da Gensichen e Lumpe (vedere il riferimento).
| Materiale | Acciaio | Modulo di elasticità | E | 210000,000 | MPa |
| Modulo di taglio | [LinkToImage01] | 81000,000 | MPa | ||
| Geometria | Cantilever tubolare | Durata | [LinkToImage01] | 4,000 | m |
| Diametro | d | 42,400 | mm | ||
| Spessore parete | t | 4,000 | mm | ||
| Carico | Momento flettente | M | 3,400 | kNm | |
Soluzione analitica
Geometricamente lineare analisi
Considerando l'analisi geometricamente lineare, il problema può essere risolto secondo l'equazione di Eulero-Bernoulli. Per la geometria, il carico e le condizioni al contorno date, l'inflessione massima risultante uz,max è la seguente:
L'inflessione ux,max considerando l'analisi geometricamente lineare è zero.
Analisi di grandi spostamenti generalizzati
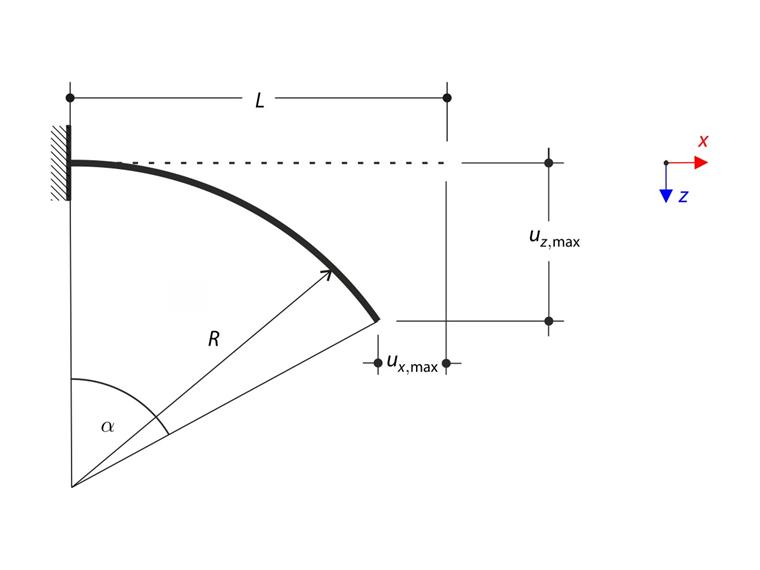
Una trave nell'analisi a grandi spostamenti è descritta dall'equazione differenziale non lineare ed è illustrata nella figura seguente.
Il termine sul lato destro è costante e di conseguenza anche il lato sinistro, che è direttamente la curvatura della trave κ, è costante. L'unica curva che ha una curvatura costante è un cerchio, quindi la soluzione a questo problema è un arco di cerchio di raggio R.
R è il raggio dell'arco di cerchio. L'angolo dell'arco di cerchio α è uguale a α=L/R.
Impostazioni di RFEM e RSTAB
- Modellato in RFEM 5.05, RSTAB 8.05 e RFEM 6.01, RSTAB 9.01
- La dimensione dell'elemento è lFE = 0,400 m
- Il numero di incrementi è 5
- Viene utilizzato il modello di materiale elastico lineare isotropo
- La rigidezza a taglio delle aste è attivata
- La divisione dell'asta per grandi spostamenti o analisi post-critica è attivata
Risultati
| ux, max [m] | Soluzione analitica | RFEM 6 | Rapporto | RSTAB 9 | Rapporto |
| Geometricamente lineare analisi | 0,000 | 0,000 | - | 0,000 | - |
| Analisi a grandi spostamenti | -0,337 | -0,336 | 0,997 | -0,336 | 0,997 |
| uz, max [m] | Soluzione analitica | RFEM 6 | Rapporto | RSTAB 9 | Rapporto |
| Geometricamente lineare analisi | 1,441 | 1,441 | 1,000 | 1,441 | 1,000 |
| Analisi a grandi spostamenti | 1,379 | 1,380 | 1,001 | 1,380 | 1,001 |
| ux, max [m] | Soluzione analitica | RFEM 5 | Rapporto | RSTAB 8 | Rapporto |
| Geometricamente lineare analisi | 0,000 | 0,000 | - | 0,000 | - |
| Analisi a grandi spostamenti | -0,337 | -0,338 | 1,003 | -0,337 | 1,000 |
| uz, max [m] | Soluzione analitica | RFEM 5 | Rapporto | RSTAB 8 | Rapporto |
| Geometricamente lineare analisi | 1,441 | 1,441 | 1,000 | 1,441 | 1,000 |
| Analisi a grandi spostamenti | 1,379 | 1,380 | 1,001 | 1,380 | 1,001 |
,_LC1__LI.jpg?mw=760&hash=8a72fd14929115d349aeafc6a154c475e761a1ac)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
