Popis
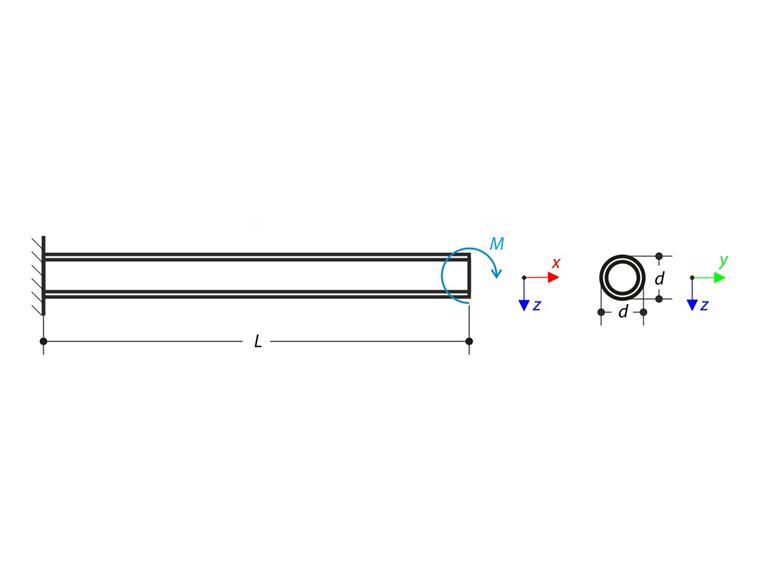
Konzola je na svém volném konci zatížena momentem M. Pomocí geometricky lineární analýzy a analýzy velkých deformací bez zanedbání vlastní tíhy nosníku stanovíme maximální průhyby ux a uz na volném konci. Verifikační příklad je založen na příkladu, který představili Gensichen a Lumpe (viz odkaz).
| Materiál | Ocel | Modul pružnosti | E | 210000,000 | MPa |
| Smykový modul | G | 81000,000 | MPa | ||
| Geometrie | Konzola z trubek | obvod | L | 4,000 | m |
| Průměr | d | 42,400 | mm | ||
| Tloušťka stěny | t | 4,000 | mm | ||
| Zatížení | Ohybový moment | W | 3,400 | kNm | |
Analytické řešení
Teorie I. řádu (geometricky lineární výpočet)
Při použití geometricky lineární analýzy lze problém vyřešit pomocí Euler-Bernoulliho rovnice. Pro danou geometrii, zatížení a okrajové podmínky je maximální průhyb uz,max následující:
Průhyb ux,max je při zohlednění geometricky lineárního výpočtu nulový.
Analýza velkých deformací
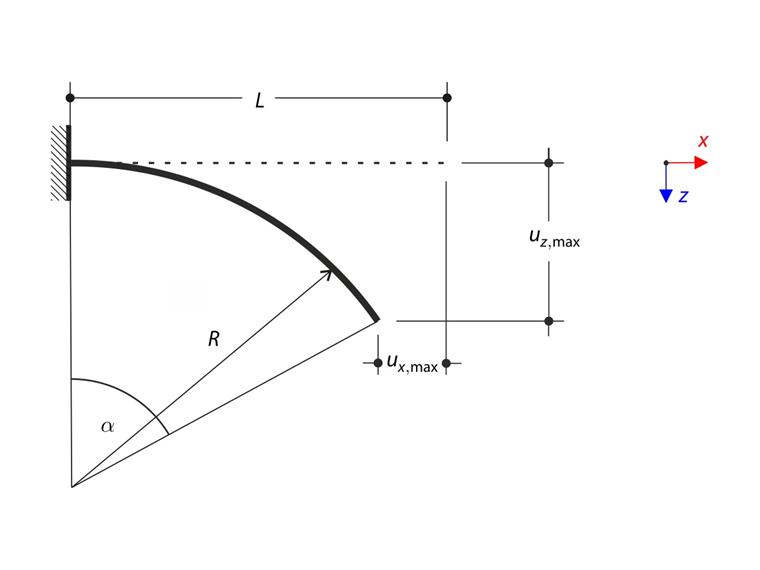
Nosník v analýze velkých deformací je popsán pomocí nelineární diferenciální rovnice a je znázorněn na následujícím obrázku.
Člen na pravé straně je konstantní, a proto je konstantní také levá strana, která je přímo zakřivením nosníku κ. Jedinou křivkou, která má konstantní zakřivení, je kružnice, a proto je řešením tohoto problému kruhový oblouk o poloměru R.
R je poloměr kruhového oblouku. Úhel kruhového oblouku α se rovná α=L/R.
Nastavení programů RFEM a RSTAB
- Modelováno v programech RFEM 5.05, RSTAB 8.05 a RFEM 6.01, RSTAB 9.01
- Velikost prvku je lFE = 0,400 m
- Počet přírůstků je 5
- Je použit izotropní lineárně elastický materiálový model
- Smyková tuhost prutů je aktivována
- Je aktivováno dělení prutu pro analýzu velkých deformací nebo postkritickou analýzu
Výsledky
| ux, max [m] | Analytické řešení | RFEM 6 | Poměrná hodnota | RSTAB 9 | Poměrná hodnota |
| Teorie I. řádu (geometricky lineární výpočet) | 0,000 | 0,000 | - | 0,000 | - |
| analýza velkých deformací | -0,337 | -0,336 | 0,997 | -0,336 | 0,997 |
| uz, max [m] | Analytické řešení | RFEM 6 | Poměrná hodnota | RSTAB 9 | Poměrná hodnota |
| Teorie I. řádu (geometricky lineární výpočet) | 1,441 | 1,441 | 1,000 | 1,441 | 1,000 |
| analýza velkých deformací | 1,379 | 1,380 | 1,001 | 1,380 | 1,001 |
| ux, max [m] | Analytické řešení | RFEM 5 | Poměrná hodnota | RSTAB 8 | Poměrná hodnota |
| Teorie I. řádu (geometricky lineární výpočet) | 0,000 | 0,000 | - | 0,000 | - |
| analýza velkých deformací | -0,337 | -0,338 | 1,003 | -0,337 | 1,000 |
| uz, max [m] | Analytické řešení | RFEM 5 | Poměrná hodnota | RSTAB 8 | Poměrná hodnota |
| Teorie I. řádu (geometricky lineární výpočet) | 1,441 | 1,441 | 1,000 | 1,441 | 1,000 |
| analýza velkých deformací | 1,379 | 1,380 | 1,001 | 1,380 | 1,001 |
,_LC1__LI.jpg?mw=760&hash=8a72fd14929115d349aeafc6a154c475e761a1ac)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
,_LC1__LI.jpg?mw=350&hash=a49d4e90c707e57dab1d5ce0c04d5d665393348d)
