项目介绍
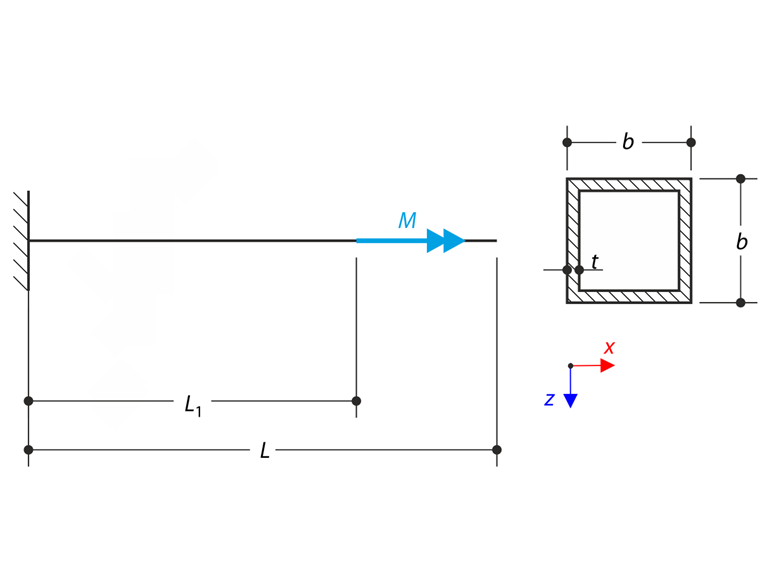
一个 QRO 型薄壁悬臂梁在左端完全固定(x=0),并且不翘曲。 在悬臂梁上施加一个在 x=L1处的扭矩 M。 下面的参数集描述了该问题。 该模型考虑了小变形,并忽略了自重。 计算最大转动 φx,max ,并控制在点 x=L1的一阶扭矩 MTpri 、二阶扭矩 MTsec和翘曲弯矩 Mω的值。 验算示例是基于 Gensichen 和 Lumpe 提出的示例(参见参考资料)。
| 材料 | 钢 | 弹性模量 | E | 210000,000 | MPa |
| 剪切模量 | G | 81000,000 | MPa | ||
| 几何尺寸 | QRO 悬臂梁 | 周长 | l | 4,000 | m |
| 宽度和高度 | b | 200,000 | mm | ||
| 墙厚度 | t | 6,000 | mm | ||
| 荷载 | 扭矩 | M | 80,000 | kNm | |
| 位置 | L1 | 2,800 | m | ||
解析解
绕 x 轴的最大转动 φx,max出现在点 x=L1并且它与自由端的值相同。
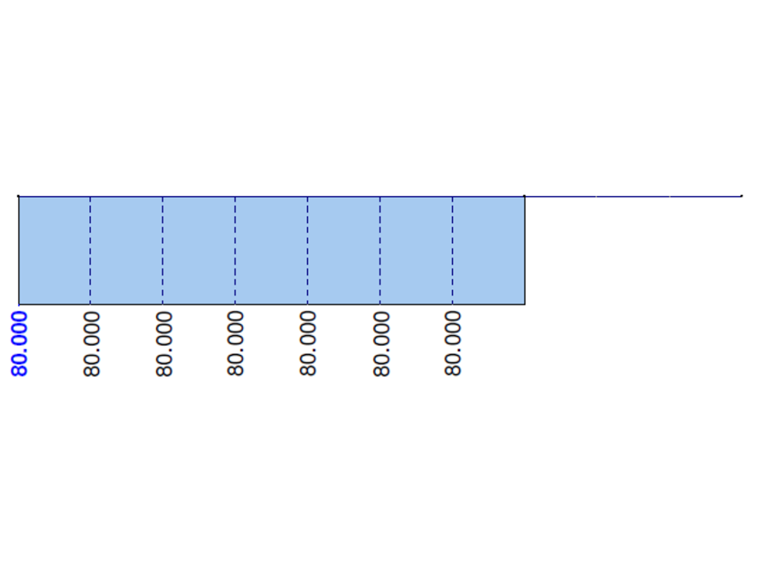
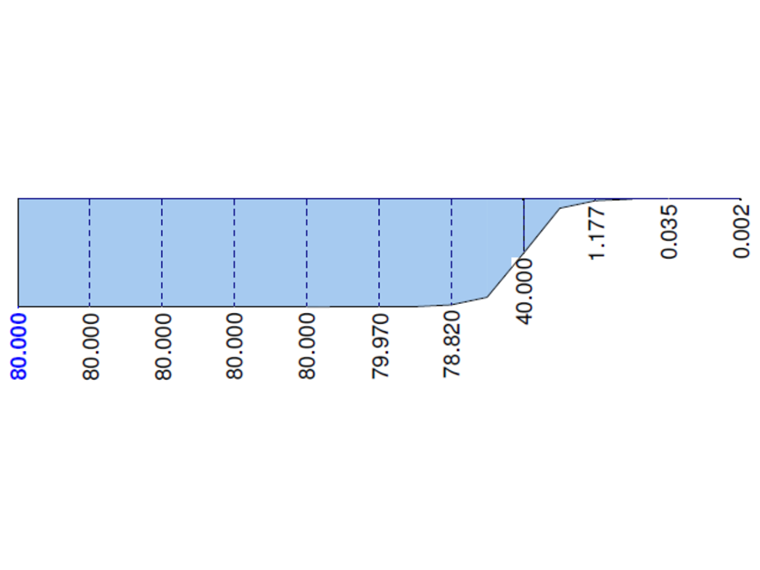
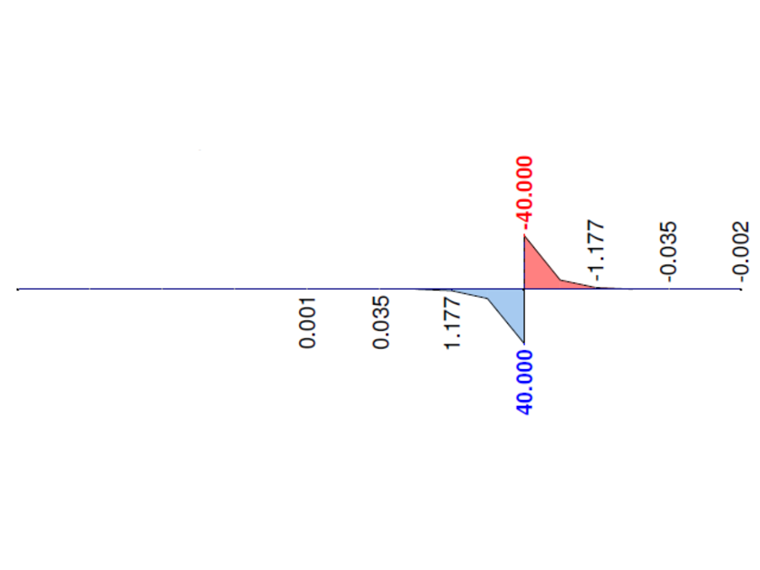
对于该薄壁型材(忽略拐角处的半径),翘曲常数 Cω =0。 因此在截面的整个长度上弯矩 MTsec和 Mω应该为零。 主扭矩 MTpri与总扭矩 MT =M 一致。
RFEM 和 RSTAB 设置
- 在RFEM 5.05、RSTAB 8.05 和 RFEM 6.01、RSTAB 9.01 中建模
- 单元尺寸 lFE = 0.200 m
- 增量数目为 5
- 使用各向同性线弹性材料模型
- 该结构是使用杆件建模的
- 使用二阶分析
- RF-FE-LTB 和 FE-LTB 模块用于 RFEM 5 和 RSTAB 8
- 在 RFEM 6 中使用了翘曲扭转和钢结构设计模块,
结果
| 解析解 | RFEM 6 | 比值 | RSTAB 9 | 比值 | |
| φx,max [弧度] | 0,063 | 0,063 | 1,000 | 0,063 | 1,000 |
| 解析解 | RFEM 5 - RF-FE-LTB | 比值 | RSTAB 8 - 有限元软件 | 比值 | |
| φx,max [弧度] | 0,063 | 0,063 | 1,000 | 0,063 | 1,000 |
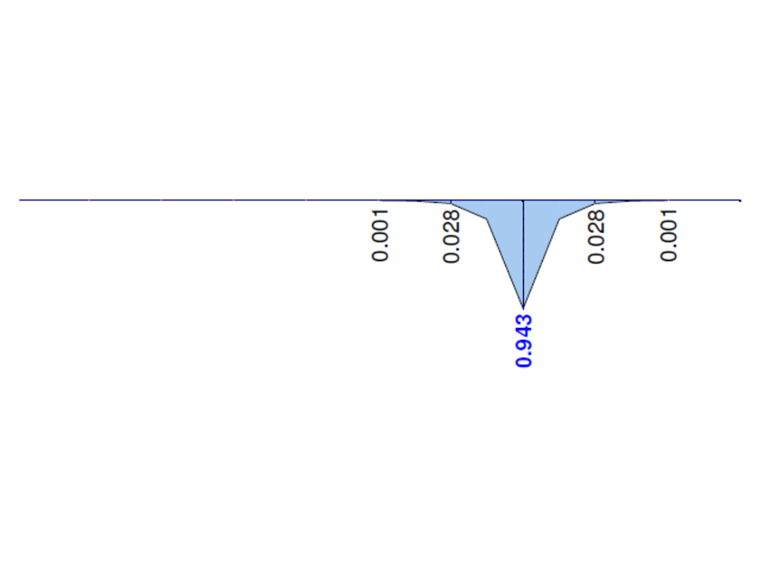
下图显示了在 RF-FE-LTB 或者 FE-LTB 模块中计算的所有给定悬臂弯矩的特性。 主扭矩 MTpri应与总扭矩 MT重合。 在截面整个长度上,弯矩 MTsec和 Mω应该为零。 可以看出,在考虑翘曲时,在加载点 x=L1附近有受影响的区域。 请注意,网格越平滑,上述影响会越来越小。
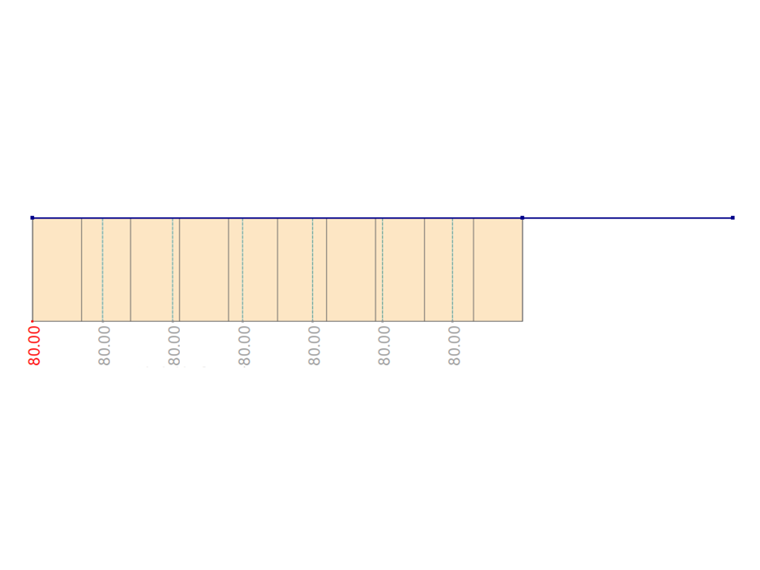
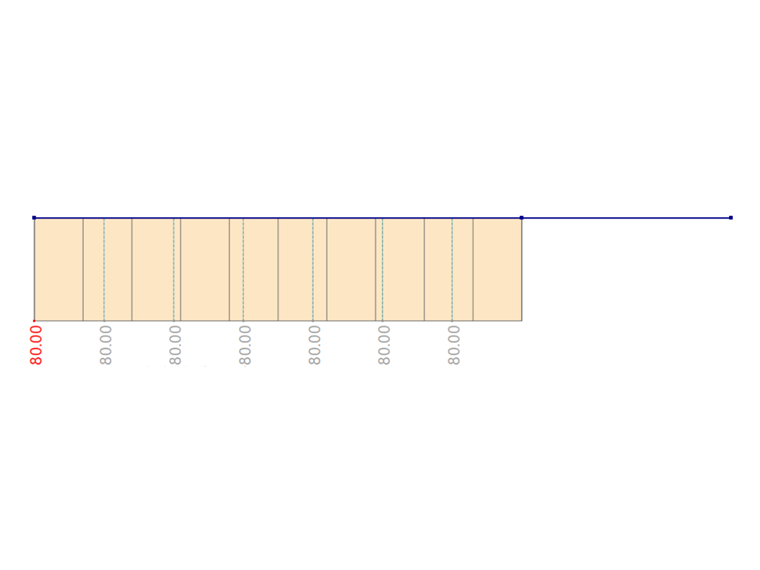
在 RFEM 6 和 RSTAB 9 中可以使用翘曲扭转模块来解决同样的问题。 计算结果如下图所示。 在RFEM 6和RSTAB 9中的结果中可以看出,离散化没有导致计算错误。


,_LC1__LI.jpg?mw=760&hash=9468a1f790362254e062fb45a395309b8eacd7fe)