Beschreibung
Am linken Ende (x=0) ist ein dünnwandiger Kragträger aus QRO-Profil vollständig befestigt und die Wölbung ist frei. The cantilever is subjected to a torque M at x=L1. Das Problem wird durch folgenden Parametersatz beschrieben. Es werden kleine Verformungen berücksichtigt und das Eigengewicht wird vernachlässigt. Es soll die maximale Verdrehung φx,max ermittelt und die Werte des primären Torsionsmomentes MTpri, sekundären Torsionsmomentes MTsec und Wölbmomentes Mω im Punkt x=L1 kontrolliert werden. Dieses Verifikationsbeispiel basiert auf dem von Gensichen und Lumpe vorgestellten Beispiel (siehe Literatur).
| Material | Stahl | Elastizitätsmodul | E | 210000,000 | MPa |
| Schubmodul | G | 81000,000 | MPa | ||
| Geometrie | QRO Kragträger | Länge | L | 4,000 | m |
| Breite und Höhe | F | 200,000 | mm | ||
| Wanddicke | t | 6,000 | mm | ||
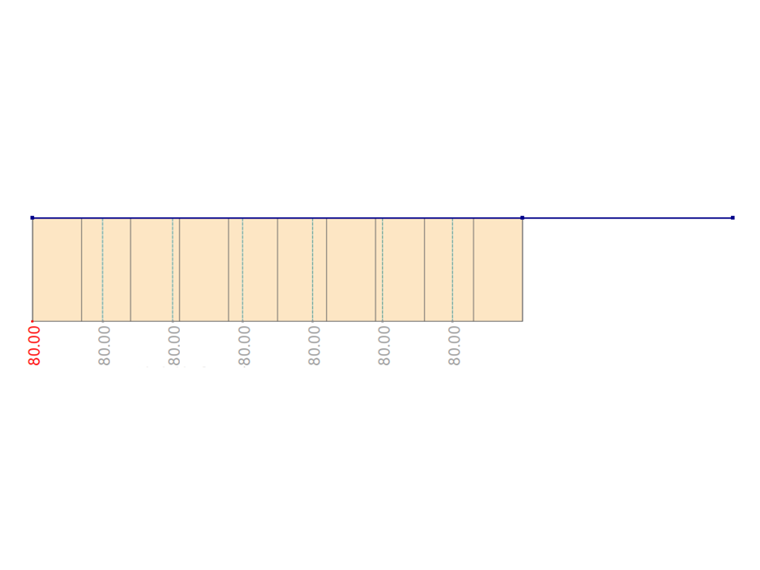
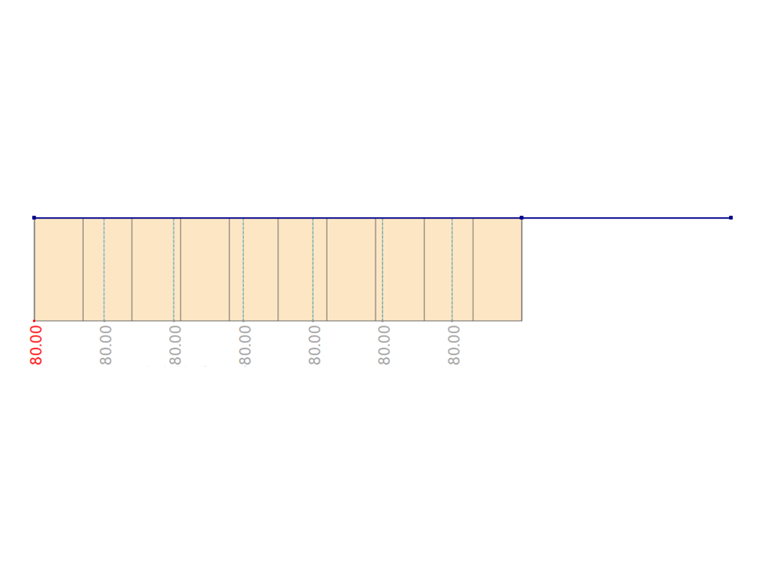
| Last | Drehmoment | M | 80,000 | kNm | |
| Lage | L1 | 2,800 | m | ||
Analytische Lösung
Die maximale Verdrehung um die x-Achse φx,max tritt im Punkt x=L1 auf und hat zum freien Ende hin den gleichen Wert.
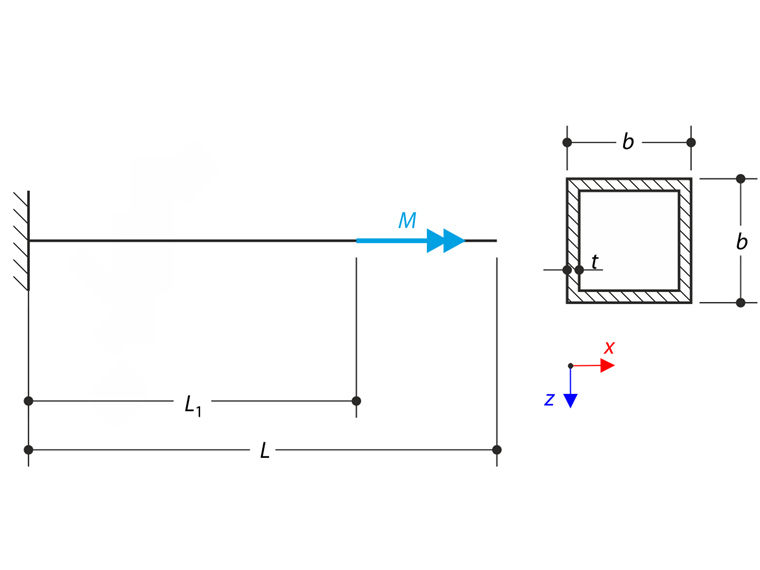
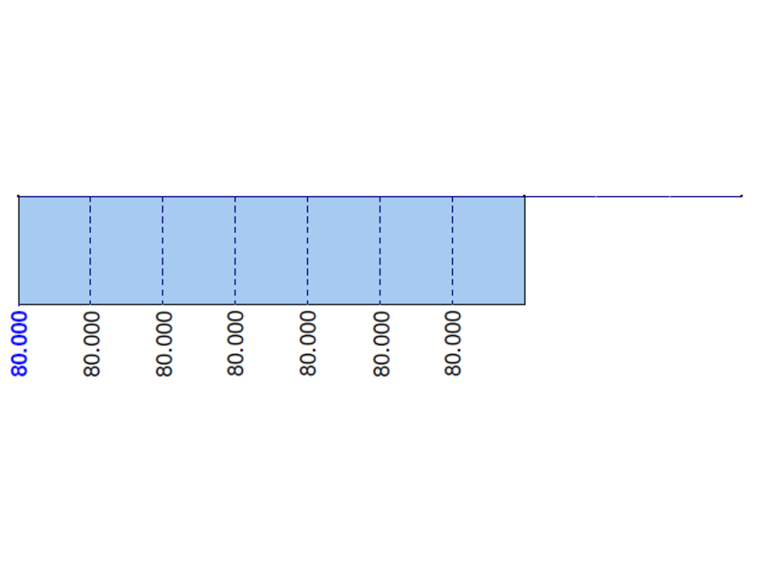
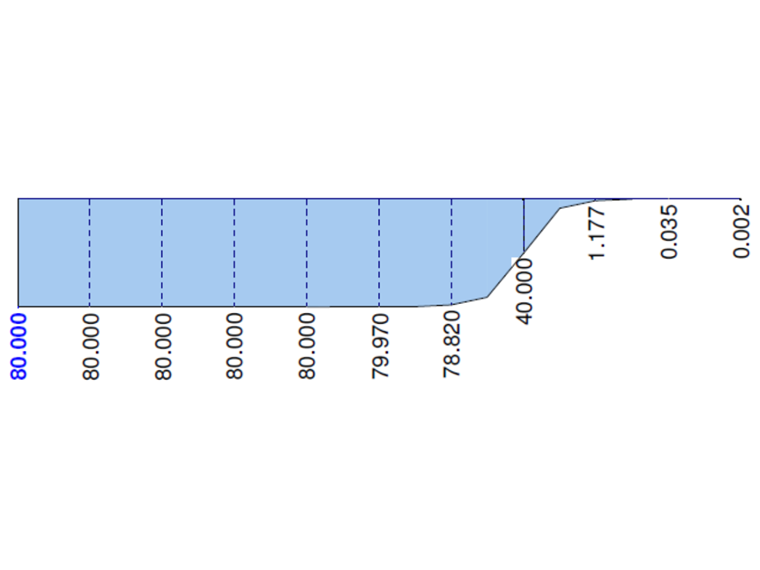
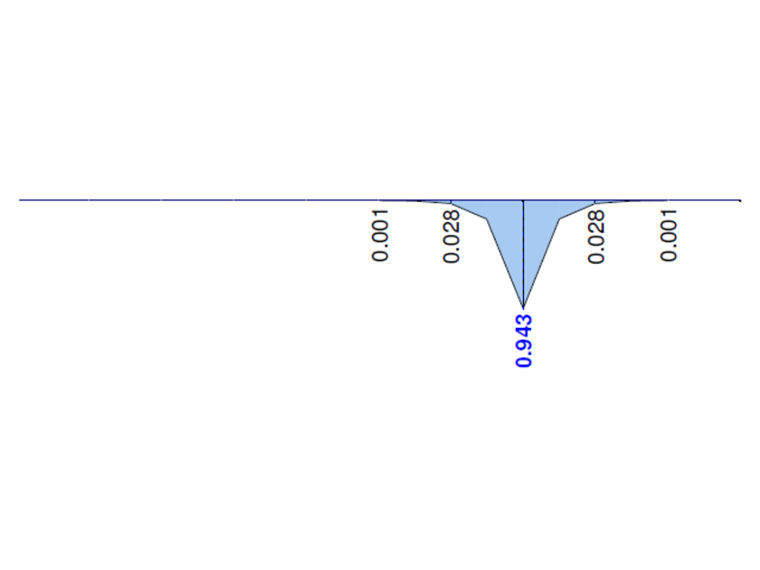
Für dieses dünnwandige Profil (Radien in den Ecken werden vernachlässigt) ist der Wölbwiderstand Cω =0. Demnach sollten die Momente MTsec und Mω auf der vollen Länge des Profils null sein. Das primäre Torsionsmoment MTpri sollte mit dem Gesamttorsionsmoment MT =M übereinstimmen.
RFEM- und RSTAB-Einstellungen
- Modelliert in RFEM 5.05, RSTAB 8.05 und RFEM 6.01, RSTAB 9.01
- The element size is lFE= 0.200 m
- Die Anzahl der Inkremente beträgt 5.
- Es wird ein isotropes linear-elastisches Materialmodell vorausgesetzt.
- Die Modellierung erfolgt über Stäbe
- Theorie II. Ordnung verwendet
- RF-FE-BGDK und FE-BGDK Modul wird in RFEM 5 und RSTAB 8 verwendet
- Das Add-On Wölbkrafttorsion und Stahlbemessung wird in RFEM 6 und 7
Ergebnisse
| Analytische Lösung | RFEM 6 | Verhältnis | RSTAB 9 | Ausnutzung | |
| φx,max [rad] | 0,063 | 0,063 | 1,000 | 0,063 | 1,000 |
| Analytische Lösung | RFEM 5 - RF-FE-BGDK | Ausnutzung | RSTAB 8 - FE-BGDK | Ausnutzung | |
| φx,max [rad] | 0,063 | 0,063 | 1,000 | 0,063 | 1,000 |
Die folgenden Grafiken zeigen das Verhalten aller Momente an einem bestimmten Kragarm, berechnet in RF-FE-BGDK bzw. FE-BGDK Modul. Das primäre Torsionsmoment MTpri sollte mit dem Gesamttorsionsmoment MT übereinstimmen. Die Momente MTsec und Mω sollten auf der vollen Länge des Profils null sein. Hier ist zu erkennen, dass der betroffene Bereich in der Nähe des Belastungspunktes x=L1 liegt, wenn dieVerwölbung berücksichtigt wird. Es ist zu beachten, dass der oben erwähnte Effekt mit je glatterem Netz geringer wird.
Die gleiche Aufgabe wird auch in RFEM 6 und RSTAB 9 mit dem Add-On Wölbkrafttorsion gelöst. Die Ergebnisse sind in den folgenden Grafiken ersichtlich. Durch die Diskretisierung entsteht in RFEM 6 und RSTAB 9 kein Rechenfehler.
,_LC1__LI.jpg?mw=760&hash=9468a1f790362254e062fb45a395309b8eacd7fe)