14235x

001519

2018-05-16

按照规范 DIN EN 1993-6 设计悬挂吊车的下翼缘

在悬挂吊车的情况下，吊车梁的下翼缘除了车轮荷载对其引起的整体的影响外，还引起了局部的翼缘弯曲。由于这些局部弯曲应力，下弦杆的作用类似于板，并且具有双轴应力条件 [1]。

承载力极限状态

必须验证，下翼缘吸收承担了车轮荷载。在[2]中第 6.7 章的公式 6.2 中，给出了以下公式：

F_{f, Rd} = \frac{l_{eff} \cdot t_{f}^{2} \cdot \frac{f_{y}}{γ_{M 0}}}{4 \cdot m} \cdot [1 - {(\frac{σ_{f, Ed}}{\frac{f_{y}}{γ_{M 0}}})}^{2}]

公式 1

值:
l_eff = 有效长度，根据[2] ，表 6.2
m = 过渡翼缘腹板上的车轮荷载杠杆臂根据[2] ，公式 6.3
σ_f,Ed = 整体荷载作用下翼缘重心轴上的弯曲应力

接着要满足下面的条件：
F_z,Ed ≤ F_f,Rd

必须考虑在跑道梁中的设计位置以及轮荷载的轴距，特别是在按照[2]中的表 6.2 计算有效长度时。

对于处于按照[2]的正常使用极限状态的悬挂起重机，有必要根据[2]的第 5.8 章计算下翼缘由车轮荷载产生的局部弯曲应力。必要系数的计算按照[2]中的表5.2进行。此外，由结构计算得出的各个全局应力必须与车轮荷载引起的局部应力叠加。

根据 EN 1993-6 中第 5.8 章的 NCI（德国），这样叠加时局部应力要折减到 75%。该验算证明了下翼缘的弹性性质。

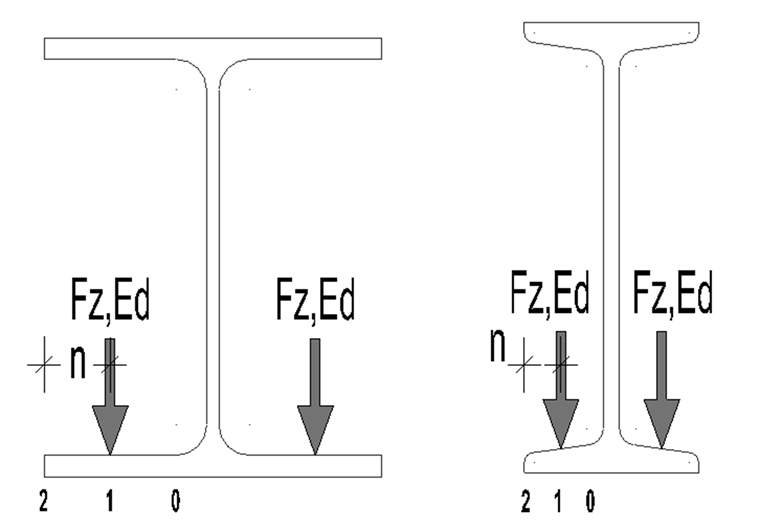
确定下翼缘局部应力的方法有很多，如文献[3]所示。在[2]中，计算按照有限元准则 9.341“梁局部应力”进行。这里应力是在局部点 0、1、2 处对应于图 01 中位置得出。

应力按照下面的公式得出：

梁纵向：

σ_{ox, Ed, ser, i} = c_{x, i} \cdot \frac{F_{z, Ed}}{t_{f}^{2}}

公式 2

梁横向：

σ_{oy, Ed, ser, i} = c_{y, i} \cdot \frac{F_{z, Ed}}{t_{f}^{2}}

公式 3

值:
cx,i 和 cy,i 按照 [2] 中表格 5.2

μ = \frac{2 \cdot n}{(b - t_{w})}

公式 4

按照 [2]，章节 5.8(4)，公式 5.7

要注意的是，临近轮的荷载距离 xw ≤ 1,5b （见图 02），分别计算每个轮的应力，然后叠加应力。见[2] , Chapter 5.8 (8)

根据[2]的第 7.5 章，在较长翼缘上的局部应力必须与结构分析得出的全局应力相叠加：

σ_{v, Ed, ser} = \sqrt{{(σ_{x, Ed, ser})}^{2} + {(σ_{y, Ed, ser})}^{2} - (σ_{x, Ed, ser}) (σ_{y, Ed, ser}) + 3 {(τ_{Ed, ser})}^{2}} \leq \frac{f_{y}}{γ_{M, s e r}}

公式 5

值:

σ_{Σx, Ed, ser} = σ_{x, Ed, ser} + 0, 75 \cdot σ_{ox, Ed, ser}

公式 6

σ_{Σy, Ed, ser} = 0, 75 \cdot σ_{oy, Ed, ser}

公式 7

设计下翼缘时要考虑几个因素。特别是有效长度的计算在吊车梁要验算的位置中起到重要作用。此外车轮的轴距很重要，临近轮的荷载距离很小时，分别计算轮的局部应力，然后叠加。

[1]	Seeßelberg, C. 克兰巴嫩： Gestaltung nach 欧洲规范 5th Bemessung und konstruktive ed. Berlin: 建筑, 2016
[2]	欧洲规范 3: 钢结构设计 - 第 6 部分：吊车支撑结构； EN 1993-6:2007 + AC:2009
[3]	Petersen, C. (1982)。 Stahlbau, 4th ed. 威斯巴登： Springer Vieweg, 2013

链接

下载

;