État limite ultime
Il faut vérifier que les charges de galets peuvent être absorbées par la membrure inférieure. Dans [2] , Chapitre 6.7, Équation 6.2, la formule suivante est donnée :
où
leff = longueur efficace selon [2] , Tableau 6.2
m = bras de levier de la charge de galet au niveau de la transition entre la semelle et l'âme selon l'Équation 6.3 de [2]
σf,Ed = contrainte de flexion dans le centre de gravité de la semelle due à la charge globale
La condition suivante doit être remplie :
Fz,Ed Ff,Rd
L'emplacement de vérification dans la poutre de roulement ainsi que l'empattement des essieux des charges de roue doivent être considérés, en particulier pour le calcul de la longueur efficace selon le Tableau 6.2 de [2].
État limite de service / à la fatigue
Pour le calcul des ponts roulants à l'état limite de service selon [2] , il est nécessaire de déterminer les contraintes locales de flexion dans la semelle inférieure dues aux charges de galets selon [2] , Chapitre 5.8. Le calcul des coefficients nécessaires est effectué selon le Tableau 5.2 de [2]. De plus, vous devez superposer les contraintes globales respectives avec les contraintes locales dues aux charges de roue dans le calcul de structure.
Selon le NCI (Allemagne) du Chapitre 5.8 de l'EN 1993-6, une réduction des contraintes locales à 75 % pour cette superposition est autorisée. Ce calcul vérifie le comportement élastique de la semelle inférieure.
Contraintes locales dans la semelle inférieure
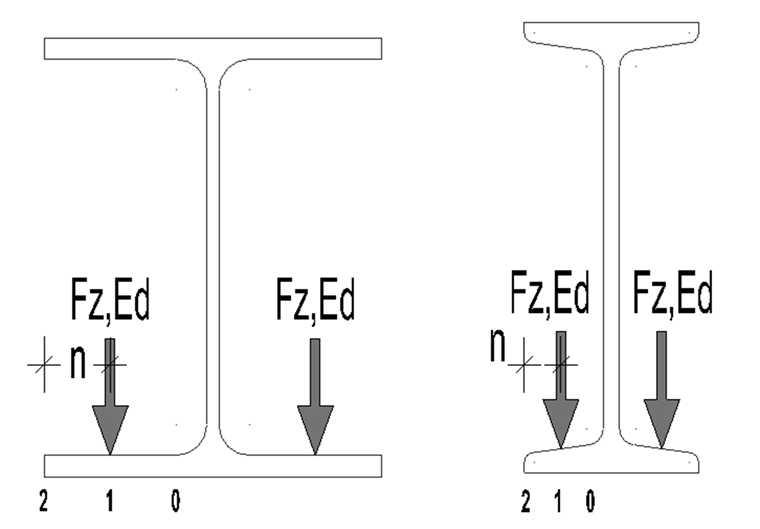
Il existe différentes méthodes pour déterminer les contraintes locales dans la semelle inférieure, qui sont également présentées dans [3]. Dans [2] , le calcul selon la directive FEM 9.341 « Contraintes locales de poutre » a été repris. Les contraintes sont calculées ici aux points locaux 0, 1 et 2, comme le montre la Figure 01.
Les contraintes sont déterminées à partir des formules suivantes :
Direction longitudinale de la poutre :
Direction transversale de la poutre :
où
cx,i and cy,i selon le Tableau 5.2 de [2]
Il convient de noter que les contraintes de chaque roue doivent être superposées dans le cas d'un empattement faible xw 1,5 b (voir la Figure 02). Voir [2] , Chapitre 5.8 (8)
Superposition avec contraintes globales
Selon le chapitre 7.5 de [2] , les contraintes locales dans la semelle la plus longue doivent être superposées aux contraintes globales du calcul de structure :
où
Résumé
Plusieurs facteurs doivent être considérés pour le calcul de la semelle inférieure. L'emplacement prévu dans la poutre de chemin de roulement joue un rôle particulièrement important dans la détermination de la longueur efficace. De plus, l'empattement des roues est important car les charges de roue et leurs contraintes locales peuvent se superposer en cas de faible distance.
![Einflussparameter für die Berechnung der effektiven Länge nach [2], Tab. 6.2](/fr/webimage/009214/476471/02-de.png?mw=760&hash=64abc6f851d1aaa6c520a53d21e6c5156792dfc3)