14380x

001519

16. Mai 2018

Nachweise für den Unterflansch von Hängekranen nach DIN EN 1993-6

Bei Hängekranen wird der Untergurt des Kranbahnträgers zusätzlich zur globalen Haupttragwirkung durch die Radlasten auf lokale Flanschbiegung beansprucht. Der Untergurt verhält sich infolge dieser lokalen Biegespannungen plattenartig und weist einen zweiachsigen Spannungszustand auf [1].

Grenzzustand der Tragfähigkeit

Es ist nachzuweisen, dass die Radlasten durch den Untergurt aufgenommen werden können. Dazu stellt [2], Kapitel 6.7, Gleichung 6.2 folgende Formel zur Verfügung:

F_{f, Rd} = \frac{l_{eff} \cdot t_{f}^{2} \cdot \frac{f_{y}}{γ_{M 0}}}{4 \cdot m} \cdot [1 - {(\frac{σ_{f, Ed}}{\frac{f_{y}}{γ_{M 0}}})}^{2}]

Formel 1

mit
l_eff = effektive Länge nach [2], Tabelle 6.2
m = Hebelarm von der Radlast zum Übergang Flansch-Steg nach [2], Gleichung 6.3
σ_f,Ed = Biegespannung in der Schwerachse des Flansches infolge globaler Beanspruchung

Belastung des Unterflansches durch Radlasten

Es ist anschließend folgende Bedingung zu erfüllen:
F_z,Ed ≤ F_f,Rd

Speziell für die Berechnung der effektiven Länge nach [2], Tabelle 6.2 sind sowohl die nachzuweisende Stelle im Kranbahnträger als auch der Achsabstand der Radlasten zu berücksichtigen.

Einflussparameter für die Berechnung der effektiven Länge nach [2], Tab. 6.2

Grenzzustand der Gebrauchstauglichkeit/Ermüdung

Für eine Bemessung von Hängekranen im Grenzzustand der Gebrauchstauglichkeit nach [2] ist es nötig, die lokalen Biegespannungen im Unterflansch infolge Radlasten nach [2], Kapitel 5.8 zu ermitteln. Die Berechnung der notwendigen Koeffizienten erfolgt nach [2], Tabelle 5.2. Weiterhin müssen die jeweiligen globalen Spannungen aus der Tragwerksberechnung mit den lokalen Spannungen infolge der Radlasten überlagert werden.

Laut NCI (Deutschland) zum Kapitel 5.8 der EN 1993-6 dürfen bei dieser Überlagerung die lokalen Spannungen auf 75 % reduziert werden. Dieser Nachweis weist das elastische Verhalten des Unterflansches nach.

Lokale Spannungen im Unterflansch

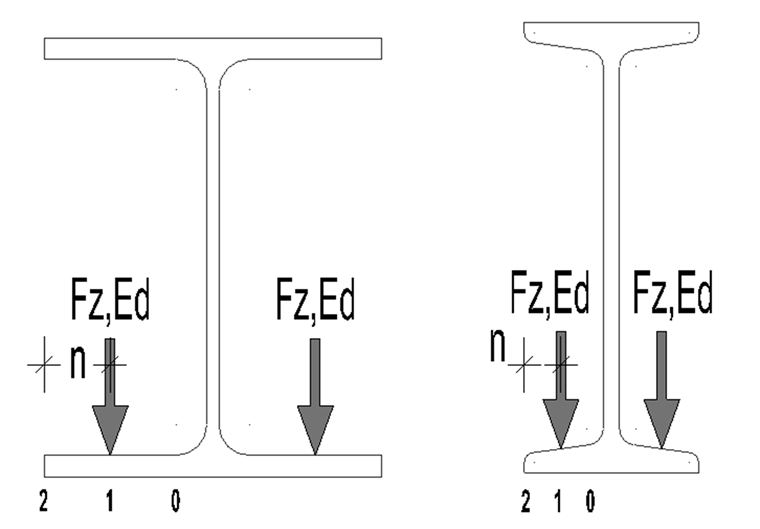
Für die Ermittlung der lokalen Spannungen im Unterflansch gibt es mehrere Verfahren, die auch in [3] dargestellt sind. In [2] wurde die Berechnung nach F.E.M.-Richtlinie 9.341 "Örtliche Trägerbeanspruchung" übernommen. Hier werden die Spannungen an den lokalen Punkten 0, 1 und 2 analog Bild 01 berechnet.

Die Spannungen ergeben sich nach den folgenden Formeln:

Längsrichtung des Trägers:

σ_{ox, Ed, ser, i} = c_{x, i} \cdot \frac{F_{z, Ed}}{t_{f}^{2}}

Formel 2

Querrichtung des Trägers:

σ_{oy, Ed, ser, i} = c_{y, i} \cdot \frac{F_{z, Ed}}{t_{f}^{2}}

Formel 3

mit
cx,i und cy,i nach [2], Tabelle 5.2

μ = \frac{2 \cdot n}{(b - t_{w})}

Formel 4

nach [2], Kapitel 5.8 (4), Gleichung 5.7

Es sei weiterhin darauf hingewiesen, dass bei kleinen Achsabständen xw ≤ 1,5 b (siehe Bild 02) die Spannungen der einzelnen Räder überlagert beziehungsweise superpositioniert werden sollten. Siehe dazu [2], Kapitel 5.8 (8)

Überlagerung mit den globalen Spannungen

Nach [2], Kapitel 7.5 sind die lokalen Spannungen im Unterflansch mit den globalen Spannungen aus der Tragwerksberechnung zu überlagern:

σ_{v, Ed, ser} = \sqrt{{(σ_{x, Ed, ser})}^{2} + {(σ_{y, Ed, ser})}^{2} - (σ_{x, Ed, ser}) (σ_{y, Ed, ser}) + 3 {(τ_{Ed, ser})}^{2}} \leq \frac{f_{y}}{γ_{M, s e r}}

Formel 5

mit

σ_{Σx, Ed, ser} = σ_{x, Ed, ser} + 0, 75 \cdot σ_{ox, Ed, ser}

Formel 6

σ_{Σy, Ed, ser} = 0, 75 \cdot σ_{oy, Ed, ser}

Formel 7

Zusammenfassung

Für die Nachweise des Unterflansches sind also einige Faktoren zu berücksichtigen. Besonders für die Ermittlung der effektiven Länge spielt die nachzuweisende Stelle im Kranbahnträger eine wichtige Rolle. Weiterhin ist der Achsstand der Räder wichtig, da bei kleinen Abständen die Radlasten und deren lokale Spannungen überlagert beziehungsweise superpositioniert werden dürfen.

Literatur

[1]	Seeßelberg, C.: Kranbahnen: Bemessung und konstruktive Gestaltung nach Eurocode, 5. Auflage. Berlin: Bauwerk, 2016
[2]	Eurocode 3: Bemessung und Konstruktion von Stahlbauten - Teil 6: Kranbahnen; EN 1993-6:2007 + AC:2009
[3]	Petersen, C.: Stahlbau, 4. Auflage. Wiesbaden: Springer Vieweg, 2013

Links

Statiksoftware für Krane und Kranbahnen

Downloads

KRANBAHN-Modelldatei

3,14 MB

;