16244x

001583

Sonja von Bloh，硕士

2023-10-12

根据 DIN EN 1993-1-2 的抗火验算

在 EN 1993-1-2 标准中，可以在 RF-/STAHL EC3 中进行防火证明。设计是根据承载能力水平的简化计算方法进行的。作为防火措施，可以选择具有不同物理特性的覆盖材料。可以选择标准温度-时间曲线、外部火曲线以及烃类火曲线来确定气体温度。

基于[3]的示例展示防火证明。

示例

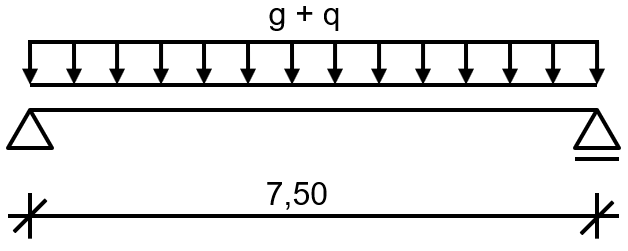
此示例包括中间楼板的次梁。为了防止侧向扭曲失稳，可以认为上翼缘被侧向固定。所需的耐火等级为R30。静态系统如图01所示。

1 结构体系与荷载

截面
- HEM 280, S235, W_pl,y = 2.966 cm³
荷载
- g_k = 16.25 kN/m（永久荷载）
- q_k = 45.0 kN/m（使用荷载类别G）

常温下的验算

关键作用是跨中弯矩。

M_{y, Ed} = (γ_{G} \cdot g_{k} γ_{Q} \cdot q_{k}) \cdot \frac{l^{2}}{8}

跨中弯矩

M_{y, Ed} = (1.35 \cdot 16.25 1.5 \cdot 45.0) \cdot \frac{7 . 50^{2}}{8} = 628.86 kNm

跨中弯矩计算

截面分类

依据[4]表5.2进行截面分类。

ε = \sqrt{\frac{235}{f_{y}}} = \sqrt{\frac{235}{235}} = 1.0

截面分类

翼缘

\frac{c}{t} = \frac{110.8}{33} = 3.36 < 9 \cdot ε = 9 \cdot 1.0 = 9

截面分类 – 翼缘

腹板

\frac{c}{t} = \frac{196}{18.5} = 10.59 < 72 \cdot ε = 72 \cdot 1.0 = 72

截面等级 - 腹板

截面可归入1类。

弯矩承载力设计值

依据[4] (6.13):

M_{c, y, Rd} = M_{pl, y, Rd} = \frac{W_{pl, y} \cdot f_{y}}{γ_{M 0}} = \frac{2966 \cdot 23.5}{1.0} \cdot 10^{- 2} = 697.01 kNm

弯矩承载力设计值

验算

依据[4] (6.12)进行验算：

\frac{M_{y, Ed}}{M_{c, y, Rd}} = \frac{628.86}{697.01} = 0.90 < 1

设计

钢材温度的确定

无保护钢构件的温升

依据[1] (4.25):

{Δθ}_{a, t} = k_{sh} \cdot \frac{\frac{A_{m}}{V}}{c_{a} \cdot ρ_{a}} \cdot {\overset{\cdot}{h}}_{net, d} \cdot Δt

k_sh	考虑屏蔽效应的修正系数
A_m/V	截面系数（表示暴露在外的地表面积与体积之比）
c_a	比热容
ρ_a	钢筋密度
Δt	时间步的间隔
h_net,d	净热通量

公式 EN 1993-1-2 (4.25)

无保护钢构件的截面因子

截面因子表示无保护的表面积与体积的比值。此处的截面因子等于钢构件截面的周长减去由地板遮挡的上翼缘宽度与截面积的比值。

\frac{A_{m}}{V} = \frac{U - b}{A} = \frac{1.69 - 0.288}{0.02402} = 58.368 1 / m

未受保护的钢构件的截面系数

包围截面的箱体的截面因子

{(\frac{A_{m}}{V})}_{b} = \frac{2 \cdot h \cdot b}{A} = \frac{2 \cdot 0.310 \cdot 0.288}{0.02402} = 37.802 1 / m

截面的长方体截面系数

考虑I型截面遮挡效应的修正因子

依据[1] (4.26a):

k_{sh} = 0.9 \cdot \frac{{(\frac{A_{m}}{V})}_{b}}{\frac{A_{m}}{V}} = 0.9 \cdot \frac{37.802}{58.368} = 0.583

工字形截面考虑阴影的修正系数

标准火灾曲线

依据[2] (3.4):

θ_{g} = 20 345 \cdot \log_{10} (8 \cdot t 1)

标准温度时间曲线

比热容

对于 20 °C ≤ θ_a < 600 °C 依据[1] (3.2a):

c_{a} = 425 7.73 \cdot 10^{- 1} \cdot θ_{a} - 1.69 \cdot 10^{- 3} \cdot θ_{a}^{2} 2.22 \cdot 10^{- 6} \cdot θ_{a}^{3}

比热容按照 EN 1993-1-2 (3.2a)

对于 600 °C ≤ θ_a < 735 °C 依据[1] (3.2b):

c_{a} = 666 \frac{13002}{738 - θ_{a}}

比热容按照 EN 1993-1-2 (3.2b)

对于 735 °C ≤ θ_a < 900 °C 依据[1] (3.2c):

c_{a} = 545 \frac{17820}{θ_{a} - 731}

比热容按照 EN 1993-1-2 (3.2c)

对于 900 °C ≤ θ_a ≤ 1.200 °C 依据[1] (3.2d):

c_{a} = 650

比热容按照 EN 1993-1-2 (3.2d)

时间步长 Δt 选择为5秒。根据[1], 章节 3.2.2(1)，钢材的密度为 ρ_a = 7,850 kg/m³。

净热流

[2] (3.1)

{\overset{\cdot}{h}}_{net} = {\overset{\cdot}{h}}_{net, c} {\overset{\cdot}{h}}_{net, r}

EN 1991-1-2 (3.1) 中的净热通量

[2] (3.2)

{\overset{\cdot}{h}}_{net, c} = α_{c} \cdot (θ_{g} - θ_{a})

α_c	标准温度时间曲线的对流传热系数 α_c = 25 W/m²K 按照 [2] 中 3.2.1 (2)

EN 1991-1-2 (3.2) 规定的净热通量

[2] (3.3)

{\overset{\cdot}{h}}_{net, r} = Φ \cdot ε_{m} \cdot ε_{f} \cdot σ \cdot [{(θ_{g} 273)}^{4} - {(θ_{a} 273)}^{4}]

ε_m	根据 [1] 中 4.2.5.1(3)，构件表面的辐射率 ε_m = 0.7
ε_f	火焰的辐射率 ε_f = 1.0参照 [1] 中 4.2.5.1(3)
σ	Stephan-Boltzmann 常数 σ = 5,67 ⋅ 10^-8 W/m² K^{4 acc.}接 [2] 中 3.1(6)
Φ	配置系数 Φ = 1.0接 [2] 中 3.1(7)

EN 1991-1-2 (3.3) 规定的净热通量

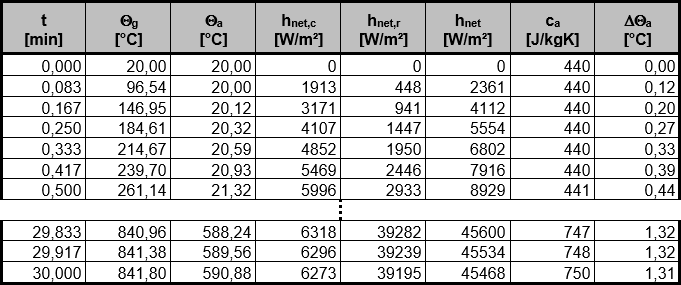
钢材温度 θ_a 和火灾气温 θ_g 的初始温度为室温20 °C。钢材温升 Δθ_a 可以逐步为每个时间段 Δt 计算。下一步骤的钢材温度由前一步的钢材温度与升温 Δθ_a 之和得出。图02部分显示了钢材温度的发展。

2 钢材温度发展图

因此，t = 30 分钟时的关键钢材温度为 θ_a = 591 °C。

火灾条件下的验算

关键作用

对于火灾设计，应采用特殊设计情况。关键作用是跨中弯矩。

M_{fi, y, Ed} = (γ_{g} \cdot g_{k} \cdot ψ_{1, 1} \cdot q_{k}) \cdot \frac{l^{2}}{8} = (1.0 \cdot 16.25 \cdot 0.5 \cdot 45.0) \cdot \frac{7 . 50^{2}}{8} = 272.46 kNm

跨中弯矩

截面分类

截面分类可以与常温下类似，但应根据[1]方程(4.2)减少的 ε 值进行。

ε = 0.85 \cdot \sqrt{\frac{235}{f_{y}}} = 0.85 \cdot \sqrt{\frac{235}{235}} = 0.85

截面等级 ε 的值

翼缘：

$\frac{c}{t} = \frac{110.8}{33} = 3.36 < 9 \cdot ε = 9 \cdot 0.85 = 7.65$

截面分类 – 翼缘
腹板：

$\frac{c}{t} = \frac{196}{18.5} = 10.59 < 72 \cdot ε = 72 \cdot 0.85 = 61.2$

截面等级 - 腹板

截面可归入1类。

弯矩承载能力的设计值

在确定弯矩承载能力的设计值时，应减少因温度升高导致的屈服强度。在钢材温度 θ_a = 591 °C 下，屈服强度的减缩因子通过插值法从[1]表3.1得出：

k_{y, θ} = 0.47 \frac{(0.78 - 0.47) \cdot (591 - 600)}{(500 - 600)} = 0.498

屈服强度的折减系数

对于受热面有三面的无保护梁，与一侧有钢筋混凝土板的配置下，调整因子 κ₁ 根据[1], 4.2.3.3(7) 为：κ₁ = 0.7

温度沿长度均匀分布。调整因子 κ₂ 为根据[1], 4.2.3.3(8) ：κ₂ = 1.0

在均匀温度分布下的弯矩承载能力设计值根据[1], 4.2.3.3 (4.8) 为：

M_{fi, y, θ, Rd} = k_{y, θ} \cdot \frac{γ_{M 0}}{γ_{M, fi}} \cdot M_{y, Rd} = 0.498 \cdot \frac{1.0}{1.0} \cdot 697.01 = 347.30 kNm

均匀温度分布时弯矩承载力设计值

在非均匀温度分布下的弯矩承载能力设计值根据[1], 4.2.3.3 (4.10) 为：

M_{fi, y, t, Rd} = \frac{M_{fi, y, θ, Rd}}{κ_{1} \cdot κ_{2}}; M_{fi, y, θ, Rd} \leq M_{y, Rd}

M_{fi, y, t, Rd} = \frac{347.30}{0.7 \cdot 1.0} = 496.15 kNm

非均匀温度分布时弯矩承载力设计值

验算

依据[1] (4.1)进行验算：

\frac{M_{fi, y, Ed}}{M_{fi, y, t, Rd}} = \frac{272.46}{496.15} = 0.55 < 1.0

设计 EN 1993-1-2 (4.1)

RF-/STAHL EC3

该示例在RF-/ STAHL EC3中进行计算。相关的RFEM和RSTAB模型文件可在文章末尾的下载中找到。

基本信息

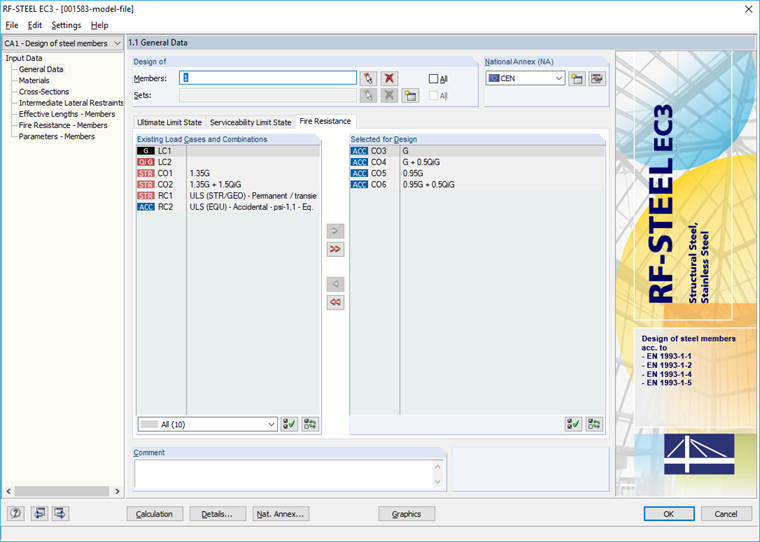
梁1将在常温下进行设计。在"承载能力"选项卡中，根据方程6.10选择针对永久/临时设计情况的荷载组合，針對火灾设计情況，在"防火"選项卡中依據方程6.11c選擇荷载组合（图03）。

3 对话框 1.1 基本输入

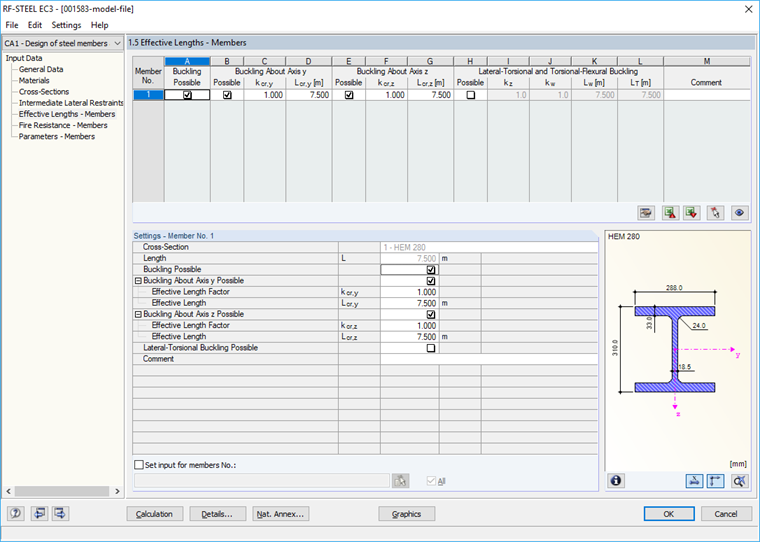
有效长度 - 梁

避免扭曲失稳，因此在"1.5 有效长度 - 梁"界面中取消选中相关选项（图04）。

4 窗口1.5有效长度 -杆件

详情

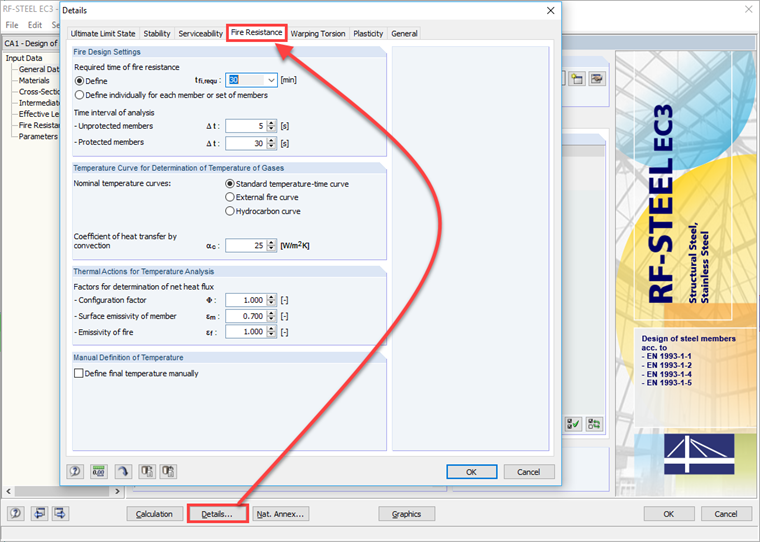
在"详情"对话框的"防火"选项卡中设置所需的防火持续时间、温度曲线和净热流的系数（图05）。

5 详细信息对话框，耐火性能选项卡：耐火性能设计

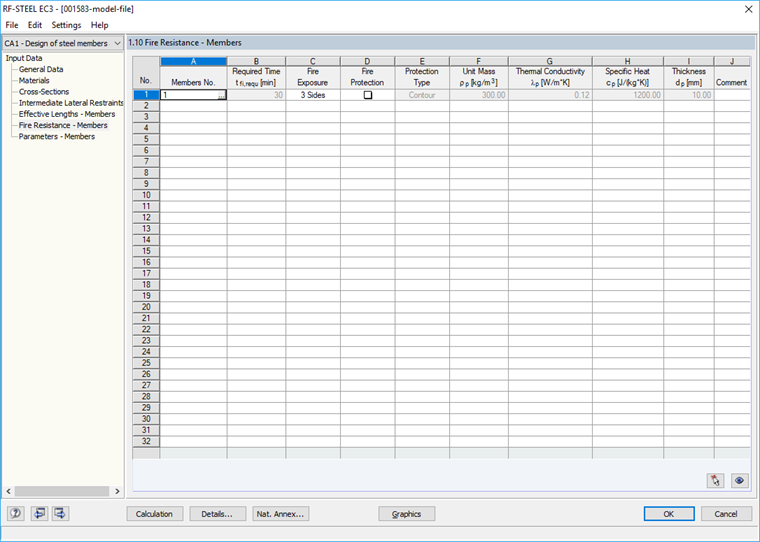
防火 - 梁

然后在"1.10 防火 - 梁"界面定义防火参数，如火灾暴露和防火措施（图06）。无保护的梁将在三个面暴露于火灾中。

6 窗口1.10 Fire Resistance -杆件

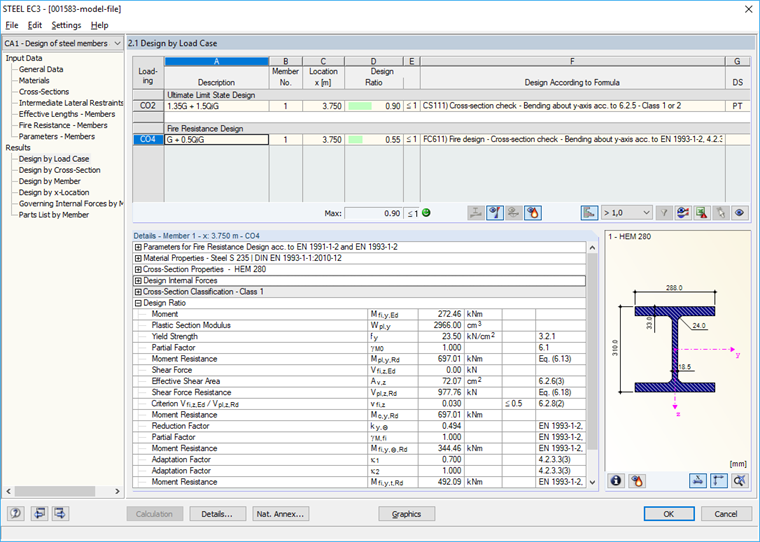
结果

计算后将显示结果（图07）。火灾设计相关的中间值如钢材温度等也将在“中间值”表格中输出。

7 结果

作者

von Bloh 女士为我们的客户提供技术支持，负责 SHAPE-THIN 软件的开发，以及钢结构和铝合金结构的开发。

链接

钢结构分析软件

参考

德国规范(1993)。欧洲规范 3： Bemessung und Konstruktion von Stahlbauten − Teil 1-2: Allgemeine Regeln - Tragwerksbemessung für den Brandfall. Beuth Verlag GmbH, Berlin, 2010.
欧洲标准化委员会 (2002)。 Eurocode 1: Einwirkungen auf Tragwerke - Teil 1-2: Allgemeine Einwirkungen - Brandeinwirkungen auf Tragwerke. Beuth Verlag GmbH, Berlin, 2002.
Mensinger, M. 和 Stadler, M. Brandschutznachweise - Workshop Eurocode 3 - Rechenbeispiele. München: Technische Universität München, Lehrstuhl für Metallbau, 2008
德国规范(1993)。欧洲规范 3： Bemessung und Konstruktion von Stahlbauten − Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau. Beuth Verlag GmbH, Berlin, 2010

下载

防火设计，防火设计，防火验算

;