13346x

001583

Sonja von Bloh, M.Sc.

2019-07-31

Fire Resistance Design According to DIN EN 1993-1-2

The fire resistance design can be performed according to EN 1993-1-2 in RF-/STEEL EC3. The design is carried out according to the simplified calculation method for the ultimate limit state. Claddings with different physical properties can be selected as fire protection measures. You can select the standard temperature-time curve, the external fire curve, and the hydrocarbon curve to determine the gas temperature.

The fire resistance design will be shown with an example from [3].

Example

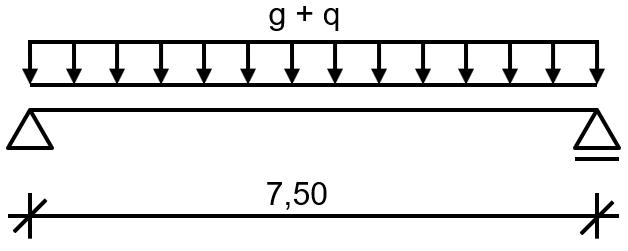
The example includes a secondary beam of an intermediate ceiling. To prevent lateral-torsional buckling, it can be assumed that the upper chord has lateral supports. The required fire resistance class is R30. The structural system is shown in Figure 01.

System and Loading

Cross-section
HEM 280, S235, W_pl,y = 2,966 cm³

Loading
g_k = 16.25 kN/m (permanent load)
q_k = 45.0 kN/m (imposed load category G)

Design with Normal Temperature Conditions

The governing action is the moment in mid-span.

M_{y, Ed} = (γ_{G} \cdot g_{k} γ_{Q} \cdot q_{k}) \cdot \frac{l^{2}}{8}

Formula 1

M_{y, Ed} = (1.35 \cdot 16.25 1.5 \cdot 45.0) \cdot \frac{7 . 50^{2}}{8} = 628.86 kNm

Formula 2

Cross-section classification

The cross-section classification is based on [4], Table 5.2.

ε = \sqrt{\frac{235}{f_{y}}} = \sqrt{\frac{235}{235}} = 1.0

Formula 3

Flange

\frac{c}{t} = \frac{110.8}{33} = 3.36 < 9 \cdot ε = 9 \cdot 1.0 = 9

Formula 4

Web

\frac{c}{t} = \frac{196}{18.5} = 10.59 < 72 \cdot ε = 72 \cdot 1.0 = 72

Formula 5

The cross-section can be assigned to class 1.

Design value of the moment resistance

M_{c, y, Rd} = M_{pl, y, Rd} = \frac{W_{pl, y} \cdot f_{y}}{γ_{M 0}} = \frac{2, 966 \cdot 23.5}{1.0} \cdot 10^{- 2} = 697.01 kNm

Formula 6

[4] (6.13)

Design

\frac{M_{y, Ed}}{M_{c, y, Rd}} = \frac{628.86}{697.01} = 0.90 < 1

Formula 7

[4] (6.12)

Determining the Steel Temperature

Temperature rise in the unprotected steel component

{Δθ}_{a, t} = k_{sh} \cdot \frac{\frac{A_{m}}{V}}{c_{a} \cdot ρ_{a}} \cdot {\overset{\cdot}{h}}_{net, d} \cdot Δt

k_sh	Correction factor for considering shadowing effect
A_m/V	Section factor (represents the ratio of the exposed surface area to the volume)
c_a	Specific heat capacity
ρ_a	Density of steel
Δt	Interval for the time step
h_net,d	Net heat flux

Equation (4.25)

[1] (4.25)

Section factor of the unprotected steel component

The section factor represents the ratio of the exposed surface area to the volume. In this case, the section factor is equal to the circumference of the steel cross-section minus the width of the upper flange, which is shaded by the ceiling, in relation to the cross-section area.

\frac{A_{m}}{V} = \frac{U - b}{A} = \frac{1.69 - 0.288}{0.02402} = 58.368 1 / m

Formula 9

Section factor for the box enclosing the section

{(\frac{A_{m}}{V})}_{b} = \frac{2 \cdot h \cdot b}{A} = \frac{2 \cdot 0, 310 \cdot 0, 288}{0, 02402} = 37, 802 1 / m

Formula 10

Correction factor for considering the shadowing effect for the I-section

k_{sh} = 0.9 \cdot \frac{{(\frac{A_{m}}{V})}_{b}}{\frac{A_{m}}{V}} = 0.9 \cdot \frac{37.802}{58.368} = 0.583

Formula 11

[1] (4.26a)

Standard temperature-time curve

θ_{g} = 20 345 \cdot \log_{10} (8 \cdot t 1)

Formula 12

[2] (3.4)

Specific heat capacity

For 20 °C ≤ θ_a < 600 °C
$c_{a} = 425 7.73 \cdot 10^{- 1} \cdot θ_{a} - 1.69 \cdot 10^{- 3} \cdot θ_{a}^{2} 2.22 \cdot 10^{- 6} \cdot θ_{a}^{3}$ Formula 13	[1] (3.2a)
For 600 °C ≤ θ_a < 735 °C
$c_{a} = 666 \frac{13, 002}{738 - θ_{a}}$ Formula 14	[1] (3.2b)
For 735 °C ≤ θ_a < 900 °C
$c_{a} = 545 \frac{17, 820}{θ_{a} - 731}$ Formula 15	[1] (3.2c)
For 900 °C ≤ θ_a ≤ 1200 °C
$c_{a} = 650$ Formula 16	[1] (3.2d)

The interval Δt for the time step method is selected as 5 s. The density of steel is ρ_a = 7,850 kg/m³ according to [1], Section 3.2.2 (1).

Net heat flux

${\overset{\cdot}{h}}_{net} = {\overset{\cdot}{h}}_{net, c} {\overset{\cdot}{h}}_{net, r}$ Formula 17	[2], (3.1)
${\overset{\cdot}{h}}_{net, c} = α_{c} \cdot (θ_{g} - θ_{a})$ Formula 18	[2], (3.2)
${\overset{\cdot}{h}}_{net, r} = Φ \cdot ε_{m} \cdot ε_{f} \cdot σ \cdot [{(θ_{g} 273)}^{4} - {(θ_{a} 273)}^{4}]$ Formula 19	[2], (3.3)

With:

α_c	convective heat transfer coefficients for the standard temperature-time curve α_c = 25 W/m²K	[2], 3.2.1(2)
ε_m	Emissivity of the structural component surface ε_m = 0.7	[1], 4.2.5.1(3)
ε_f	Emissivity of a flame ε_f = 1.0	[1], 4.2.5.1(3)
σ	the Stephan-Boltzmann constant σ = 5.67 ⋅ 10^-8 W/m²K⁴	[2], 3.1(6)
Φ	Configuration factor Φ = 1.0	[2], 3.1(7)

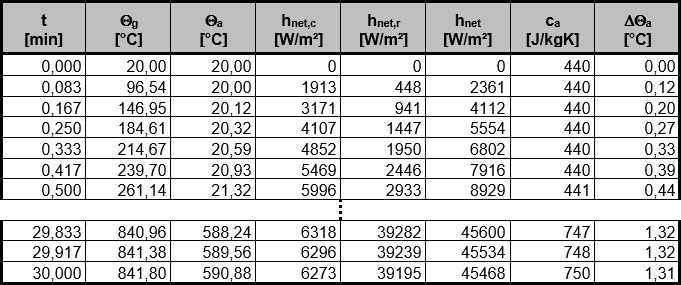
For the steel temperature θ_a and the fire gas temperature θ_g, the start temperature is assumed to be room temperature of 20 °C. The increase of temperature for the steel Δθ_a can be calculated step by step for each time interval Δt. The steel temperature for the next time step is obtained from the sum of the steel temperature of the previous step and the heating Δθ_a. Figure 02 shows a partial view of the development of the steel temperature.

Development of Steel Temperature

Thus, the governing steel temperature at the point of time t = 30 min is θ_a = 591 °C.

Design for Fire Situation

Governing action

The accidental design situation has to be used for the fire resistance design. The governing action is the moment in mid-span.

M_{fi, y, Ed} = (γ_{g} \cdot g_{k} ψ_{1, 1} \cdot q_{k}) \cdot \frac{l^{2}}{8} = (1.0 \cdot 16.25 0.5 \cdot 45.0) \cdot \frac{7 . 50^{2}}{8} = 272.46 kNm

Formula 20

Cross-section classification

For the purposes of these simplified rules the cross-sections may be classified as for normal temperature design with a reduced value for ε as given in [1], Equation (4.2).

ε = 0.85 \cdot \sqrt{\frac{235}{f_{y}}} = 0.85 \cdot \sqrt{\frac{235}{235}} = 0.85

Formula 21

Flange

\frac{c}{t} = \frac{110.8}{33} = 3.36 < 9 \cdot ε = 9 \cdot 0.85 = 7.65

Formula 22

Web

\frac{c}{t} = \frac{196}{18.5} = 10.59 < 72 \cdot ε = 72 \cdot 0.85 = 61.2

Formula 23

The cross-section can be assigned to class 1.

Design value of the moment resistance

When determining the design value of the moment resistance, it is necessary to reduce the yield strength due to the increased temperature. For steel temperature θ_a = 591 °C, the reduction factor for the yield strength interpolated from [1], Table 3.1 results in:

k_{y, θ} = 0.47 \frac{(0.78 - 0.47) \cdot (591 - 600)}{(500 - 600)} = 0.498

Formula 24

For the unprotected beam with a reinforced concrete slab on one side and fire exposure on the other three sides, the adaptation factor κ₁ according to [1], 4.2.3.3 (7) results in:

κ₁ = 0.7

The temperature is distributed uniformly over the length. The adjustment factor κ₂ according to [1], 4.2.3.3 (8) results in:

κ₂ = 1.0

The design value of the moment resistance with uniform temperature distribution according to [1], 4.2.3.3 (4.8) results in:

M_{fi, y, θ, Rd} = k_{y, θ} \cdot \frac{γ_{M 0}}{γ_{M, fi}} \cdot M_{y, Rd} = 0.498 \cdot \frac{1.0}{1.0} \cdot 697.01 = 347.30 kNm

Formula 25

The design value of the moment resistance with non-uniform temperature distribution according to [1], 4.2.3.3 (4.10) results in:

M_{fi, y, t, Rd} = \frac{M_{fi, y, θ, Rd}}{κ_{1} \cdot κ_{2}} mit M_{fi, y, θ, Rd} \leq M_{y, Rd}

Formula 26

M_{fi, y, t, Rd} = \frac{347.30}{0.7 \cdot 1.0} = 496.15 kNm

Formula 27

Design

\frac{M_{fi, y, Ed}}{M_{fi, y, t, Rd}} = \frac{272.46}{496.15} = 0.55 < 1.0

Formula 28

[1] (4.1)

RF-/STEEL EC3

The example is calculated in RF-/STEEL EC3. You can download the corresponding model files for RFEM and RSTAB at the end of this article.

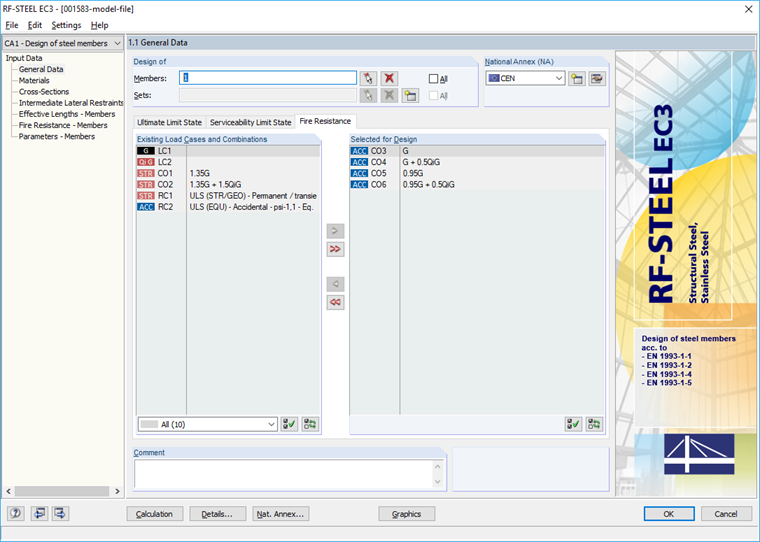
General Data: Member 1 will be designed. For the design under normal temperature, select the load combinations for the permanent/transient design situation according to Equation 6.10 in the "Ultimate Limit State" tab and the load combinations for the accidental design situation according to Equation 6.11c for the fire resistance design in the "Fire Resistance" tab (Figure 03).

Window 1.1 General Data

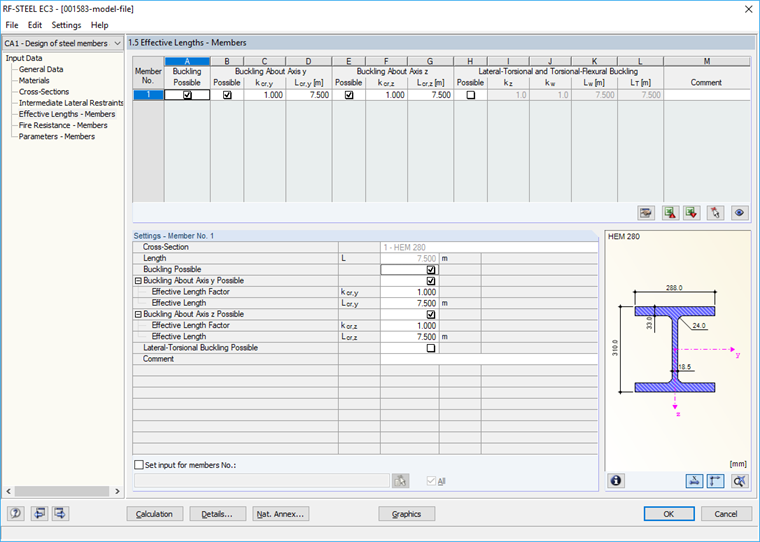
Effective Lengths - Members: Lateral-torsional and torsional-flexural buckling is prevented so that the corresponding check box is cleared in Window "1.5 Effective Lengths - Members" (Figure 04).

Window 1.5 Effective Lengths - Members

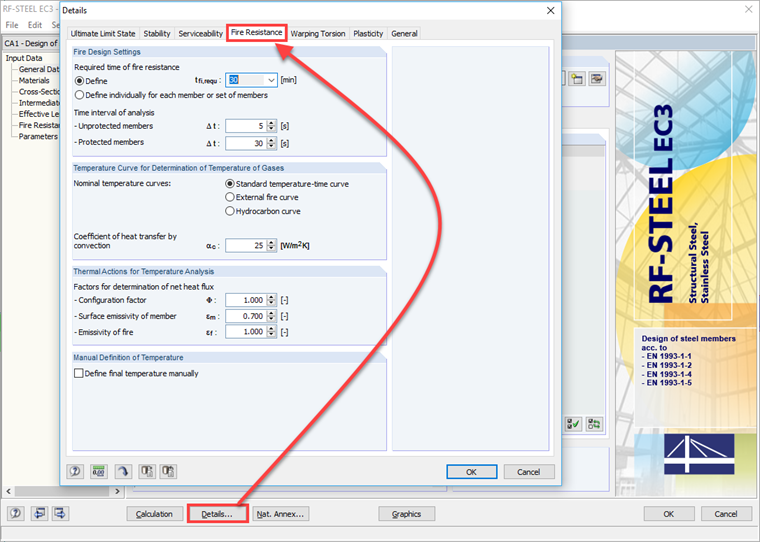
Details: The required time of fire resistance, the temperature curve, and the coefficients to determine the net heat flux are defined in the "Fire Resistance" tab of the "Details" dialog box (Figure 05).

Details Dialog Box, Fire Resistance Tab: Settings for Fire Design

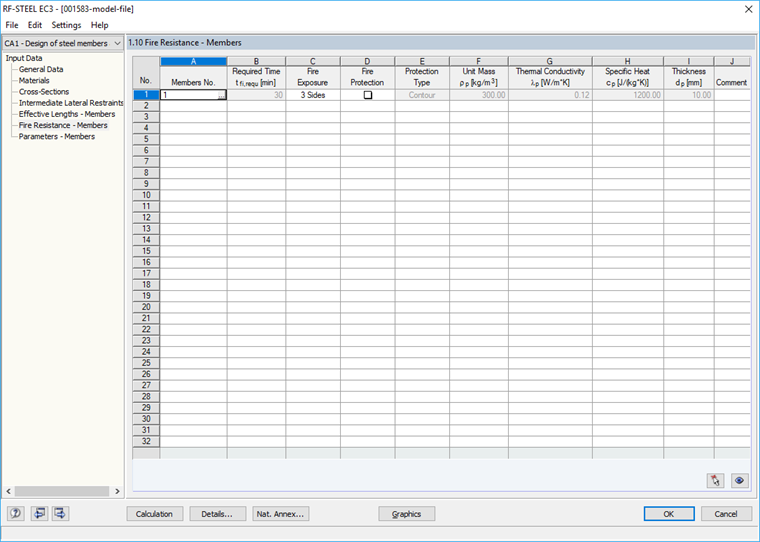
Fire Resistance - Members: Define the fire resistance parameters such as fire exposure and fire protection measures in the "1.10 Fire Resistance - Members" window (Figure 06). The unprotected beam is exposed to fire on three sides.

Window 1.10 Fire Resistance - Members

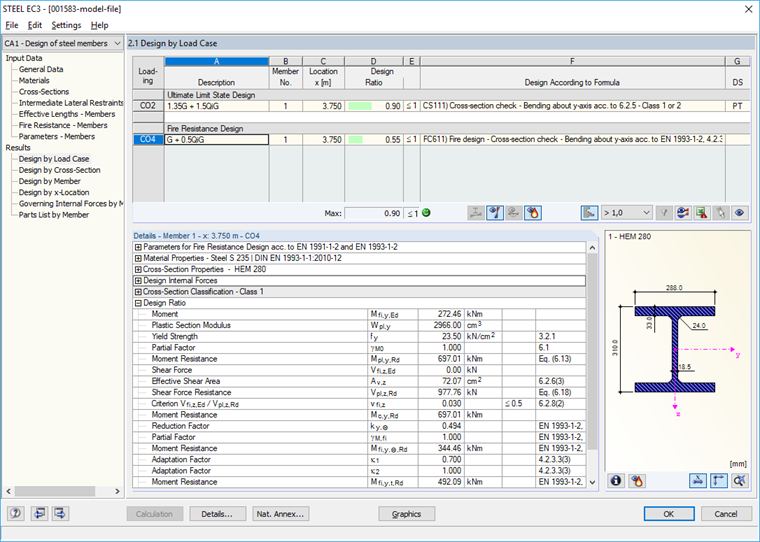
Results: The results are displayed after the calculation (Figure 07). The intermediate values relevant for the fire resistance design, such as steel temperature, are also displayed in the "Details" table.

Results

Author

Ms. von Bloh provides technical support for our customers and is responsible for the development of the SHAPE‑THIN program as well as steel and aluminum structures.

Links

Structural Analysis Software for Steel Structures

References

European Committee for Standardization (2005). Eurocode 3: Design of Steel Structures – Part 1-2: General Rules – Structural Fire Design, EN 1993-1-2. Berlin: Beuth.
European Committee for Standardization (2002). Eurocode 1: Actions on Structures – Part 1-2: General Actions – Actions on Structures Exposed to Fire, EN 1991-1-2. Berlin: Beuth.
Mensinger, M.; Stadler, M.: Brandschutznachweise - Workshop Eurocode 3 - Rechenbeispiele. München: Technische Universität München, Lehrstuhl für Metallbau, 2008
European Committee for Standardization (CEN). (2010). Eurocode 3: Design of Steel Structures – Part 1‑1: General Rules and Rules for Buildings, EN 1993‑1‑1:2010‑12. Berlin: Beuth Verlag GmbH.

Downloads

;