14130x

001583

Sonja von Bloh, M.Sc.

31. Juli 2019

Brandschutznachweis nach DIN EN 1993-1-2

Der Brandschutznachweis kann in RF-/STAHL EC3 nach EN 1993-1-2 geführt werden. Die Bemessung erfolgt nach dem vereinfachten Berechnungsverfahren auf der Tragfähigkeitsebene. Als Brandschutzmaßnahmen können Bekleidungen mit verschiedenen physikalischen Eigenschaften gewählt werden. Es stehen die Einheits-Temperaturzeitkurve, Außenbrandkurve sowie die Hydrokarbon-Brandkurve für die Ermittlung der Gastemperatur zur Auswahl.

Der Brandschutznachweis wird anhand eines Beispiels aus [3] gezeigt.

Beispiel

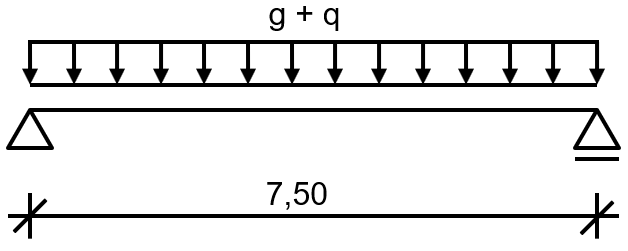
Das Beispiel umfasst einen Nebenträger einer Zwischendecke. Der Obergurt kann zur Verhinderung von Biegedrillknicken als seitlich gehalten betrachtet werden. Die erforderliche Feuerwiderstandsklasse beträgt R30. Das statische System ist in Bild 01 dargestellt.

1 System und Belastung

Querschnitt
- HEM 280, S235, W_pl,y = 2.966 cm³
Belastung
- g_k = 16,25 kN/m (ständige Last)
- q_k = 45,0 kN/m (Nutzlast Kategorie G)

Nachweis unter Normaltemperatur

Maßgebende Einwirkung ist das Moment in Feldmitte.

M_{y, Ed} = (γ_{G} \cdot g_{k} γ_{Q} \cdot q_{k}) \cdot \frac{l^{2}}{8}

Moment in Feldmitte

M_{y, Ed} = (1.35 \cdot 16.25 1.5 \cdot 45.0) \cdot \frac{7 . 50^{2}}{8} = 628.86 kNm

Berechnung des Moments in Feldmitte

Querschnittsklassifizierung

Die Querschnittsklassifizierung wird gemäß [4], Tabelle 5.2 vorgenommen.

ε = \sqrt{\frac{235}{f_{y}}} = \sqrt{\frac{235}{235}} = 1.0

Querschnittsklassifizierung

Flansch

\frac{c}{t} = \frac{110.8}{33} = 3.36 < 9 \cdot ε = 9 \cdot 1.0 = 9

Querschnittsklassifizierung – Flansch

Steg

\frac{c}{t} = \frac{196}{18.5} = 10.59 < 72 \cdot ε = 72 \cdot 1.0 = 72

Querschnittsklassifizierung – Steg

Der Querschnitt kann der Klasse 1 zugeordnet werden.

Bemessungswert der Momentenbeanspruchbarkeit

nach [4] (6.13):

M_{c, y, Rd} = M_{pl, y, Rd} = \frac{W_{pl, y} \cdot f_{y}}{γ_{M 0}} = \frac{2966 \cdot 23.5}{1.0} \cdot 10^{- 2} = 697.01 kNm

Bemessungswert der Momentenbeanspruchbarkeit

Nachweis

Nachweis nach [4] (6.12):

\frac{M_{y, Ed}}{M_{c, y, Rd}} = \frac{628.86}{697.01} = 0.90 < 1

Nachweis

Ermittlung der Stahltemperatur

Temperaturanstieg im ungeschützten Stahlbauteil

nach [1] (4.25):

{Δθ}_{a, t} = k_{sh} \cdot \frac{\frac{A_{m}}{V}}{c_{a} \cdot ρ_{a}} \cdot {\overset{\cdot}{h}}_{net, d} \cdot Δt

k_sh	Korrekturfaktor zur Berücksichtigung des Abschattungseffekts
A_m/V	Profilfaktor (gibt das Verhältnis der ungeschützten Oberfläche zum Volumen wieder)
c_a	Spezifische Wärmekapazität
ρ_a	Dichte des Stahls
Δt	Intervall für den Zeitschritt
h_net,d	Netto-Wärmestrom

Gleichung EN 1993-1-2 (4.25)

Profilfaktor des ungeschützten Stahlbauteils

Der Profilfaktor gibt das Verhältnis der ungeschützten Oberfläche zum Volumen wieder. Der Profilfaktor ist hier gleich dem Umfang des Stahlprofils abzüglich der Breite des oberen Flansches, der durch die Decke abgeschattet ist, im Verhältnis zur Querschnittsfläche.

\frac{A_{m}}{V} = \frac{U - b}{A} = \frac{1.69 - 0.288}{0.02402} = 58.368 1 / m

Profilfaktor des ungeschützten Stahlbauteils

Profilfaktor für den das Profil umschließenden Kasten

{(\frac{A_{m}}{V})}_{b} = \frac{2 \cdot h \cdot b}{A} = \frac{2 \cdot 0.310 \cdot 0.288}{0.02402} = 37.802 1 / m

Profilfaktor für den das Profil umschließenden Kasten

Korrekturfaktor zur Berücksichtigung des Abschattungseffekts für I-Profil

nach [1] (4.26a):

k_{sh} = 0.9 \cdot \frac{{(\frac{A_{m}}{V})}_{b}}{\frac{A_{m}}{V}} = 0.9 \cdot \frac{37.802}{58.368} = 0.583

Korrekturfaktor zur Berücksichtigung des Abschattungseffekts für I-Profil

Einheits-Temperaturzeitkurve

nach [2] (3.4):

θ_{g} = 20 345 \cdot \log_{10} (8 \cdot t 1)

Einheits-Temperaturzeitkurve

Spezifische Wärmekapazität

Für 20 °C ≤ θ_a < 600 °C nach [1] (3.2a):

c_{a} = 425 7.73 \cdot 10^{- 1} \cdot θ_{a} - 1.69 \cdot 10^{- 3} \cdot θ_{a}^{2} 2.22 \cdot 10^{- 6} \cdot θ_{a}^{3}

Spezifische Wärmekapazität nach EN 1993-1-2 (3.2a)

Für 600 °C ≤ θ_a < 735 °C nach [1] (3.2b):

c_{a} = 666 \frac{13002}{738 - θ_{a}}

Spezifische Wärmekapazität nach EN 1993-1-2 (3.2b)

Für 735 °C ≤ θ_a < 900 °C nach [1] (3.2c):

c_{a} = 545 \frac{17820}{θ_{a} - 731}

Spezifische Wärmekapazität nach EN 1993-1-2 (3.2c)

Für 900 °C ≤ θ_a ≤ 1.200 °C nach [1] (3.2d):

c_{a} = 650

Spezifische Wärmekapazität nach EN 1993-1-2 (3.2d)

Die Schrittweite Δt für das Zeitschrittverfahren wird zu 5 s gewählt. Die Rohdichte von Stahl beträgt gemäß [1], Abschnitt 3.2.2(1) ρ_a = 7.850 kg/m³.

Netto-Wärmestrom

[2] (3.1)

{\overset{\cdot}{h}}_{net} = {\overset{\cdot}{h}}_{net, c} {\overset{\cdot}{h}}_{net, r}

Netto-Wärmestrom nach EN 1991-1-2 (3.1)

[2] (3.2)

{\overset{\cdot}{h}}_{net, c} = α_{c} \cdot (θ_{g} - θ_{a})

α_c	Konvektiver Wärmeübergangskoeffizienten für die Einheits- Temperaturzeitkurve α_c = 25 W/m²K nach [2], 3.2.1(2)

Netto-Wärmestrom nach EN 1991-1-2 (3.2)

[2] (3.3)

{\overset{\cdot}{h}}_{net, r} = Φ \cdot ε_{m} \cdot ε_{f} \cdot σ \cdot [{(θ_{g} 273)}^{4} - {(θ_{a} 273)}^{4}]

ε_m	Emissivität der Bauteiloberfläche ε_m = 0,7 nach [1], 4.2.5.1(3)
ε_f	Emissivität der Flamme ε_f = 1,0 nach [1], 4.2.5.1(3)
σ	Stephan-Boltzmann-Konstante σ = 5,67 ⋅ 10^-8 W/m²K⁴ nach [2], 3.1(6)
Φ	Konfigurationsfaktor Φ = 1,0 nach [2], 3.1(7)

Netto-Wärmestrom nach EN 1991-1-2 (3.3)

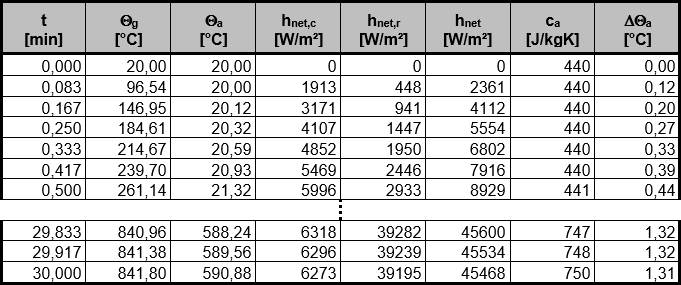
Für die Stahltemperatur θ_a und Brandgastemperatur θ_g wird als Anfangstemperatur von Raumtemperatur 20 °C ausgegangen. Die Erwärmung des Stahls Δθ_a kann schrittweise für jeden Zeitabschnitt Δt berechnet werden. Die Stahltemperatur für den nächsten Zeitschritt ergibt sich aus der Summe der Stahltemperatur des vorhergehenden Schritts und der Erwärmung Δθ_a. In Bild 02 ist ausschnittsweise die Entwicklung der Stahltemperatur wiedergegeben.

2 Entwicklung der Stahltemperatur

Die maßgebende Stahltemperatur zum Zeitpunkt t = 30 min beträgt somit θ_a = 591 °C.

Nachweis im Brandfall

Maßgebende Einwirkung

Für die Brandbemessung ist die außergewöhnliche Bemessungssituation heranzuziehen. Maßgebende Einwirkung ist das Moment in Feldmitte.

M_{fi, y, Ed} = (γ_{g} \cdot g_{k} \cdot ψ_{1, 1} \cdot q_{k}) \cdot \frac{l^{2}}{8} = (1.0 \cdot 16.25 \cdot 0.5 \cdot 45.0) \cdot \frac{7 . 50^{2}}{8} = 272.46 kNm

Moment in Feldmitte

Querschnittsklassifizierung

Die Querschnittsklassifizierung darf wie unter Normaltemperatur, jedoch mit einem nach [1], Gleichung (4.2) abgeminderten Wert für ε durchgeführt werden.

ε = 0.85 \cdot \sqrt{\frac{235}{f_{y}}} = 0.85 \cdot \sqrt{\frac{235}{235}} = 0.85

Wert ε für Querschnittsklassifizierung

Flansch:

$\frac{c}{t} = \frac{110.8}{33} = 3.36 < 9 \cdot ε = 9 \cdot 0.85 = 7.65$

Querschnittsklassifizierung – Flansch
Steg:

$\frac{c}{t} = \frac{196}{18.5} = 10.59 < 72 \cdot ε = 72 \cdot 0.85 = 61.2$

Querschnittsklassifizierung – Steg

Der Querschnitt kann der Klasse 1 zugeordnet werden.

Bemessungswert der Momententragfähigkeit

Bei der Ermittlung des Bemessungswertes der Momententragfähigkeit muss die Streckgrenze aufgrund der erhöhten Temperatur abgemindert werden. Bei einer Stahltemperatur θ_a = 591 °C ergibt sich der Abminderungsfaktor für die Streckgrenze interpoliert aus [1], Tabelle 3.1 zu:

k_{y, θ} = 0.47 \frac{(0.78 - 0.47) \cdot (591 - 600)}{(500 - 600)} = 0.498

Abminderungsfaktor für die Streckgrenze

Für den ungeschützten Träger mit einer Stahlbetonplatte auf der einen Seite und Brandbeanspruchung auf den drei anderen Seiten ergibt sich der Anpassungsfaktor κ₁ gemäß [1], 4.2.3.3(7) zu:
κ₁ = 0,7

Die Temperatur ist über die Länge gleichmäßig verteilt. Es ergibt sich der Anpassungsfaktor κ₂ gemäß [1], 4.2.3.3(8) zu:
κ₂ = 1,0

Der Bemessungswert der Momententragfähigkeit mit gleichmäßiger Temperaturverteilung ergibt sich gemäß [1], 4.2.3.3 (4.8) zu:

M_{fi, y, θ, Rd} = k_{y, θ} \cdot \frac{γ_{M 0}}{γ_{M, fi}} \cdot M_{y, Rd} = 0.498 \cdot \frac{1.0}{1.0} \cdot 697.01 = 347.30 kNm

Bemessungswert der Momententragfähigkeit mit gleichmäßiger Temperaturverteilung

Der Bemessungswert der Momententragfähigkeit mit ungleichmäßiger Temperaturverteilung ergibt sich gemäß [1], 4.2.3.3 (4.10) zu:

M_{fi, y, t, Rd} = \frac{M_{fi, y, θ, Rd}}{κ_{1} \cdot κ_{2}}; M_{fi, y, θ, Rd} \leq M_{y, Rd}

M_{fi, y, t, Rd} = \frac{347.30}{0.7 \cdot 1.0} = 496.15 kNm

Bemessungswert der Momententragfähigkeit mit ungleichmäßiger Temperaturverteilung

Nachweis

Nachweis nach [1] (4.1):

\frac{M_{fi, y, Ed}}{M_{fi, y, t, Rd}} = \frac{272.46}{496.15} = 0.55 < 1.0

Nachweis EN 1993-1-2 (4.1)

RF-/STAHL EC3

Das Beispiel wird in RF-/ STAHL EC3 berechnet. Die zugehörigen Modelldateien für RFEM und RSTAB finden sich unter Downloads am Ende des Beitrages.

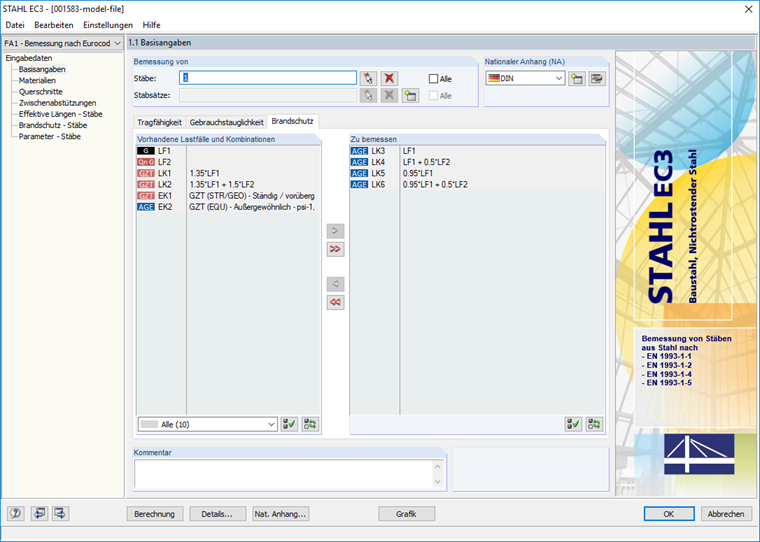
Basisangaben

Bemessen wird der Stab 1. Für die Bemessung unter Normaltemperatur werden im Register "Tragfähigkeit" die Lastkombinationen für die ständige/vorübergehende Bemessungssituation nach Gleichung 6.10 und für die Brandbemessung werden im Register "Brandschutz" die Lastkombinationen für die außergewöhnliche Bemessungssituation nach Gleichung 6.11c ausgewählt (Bild 03).

3 Maske 1.1 Basisangaben

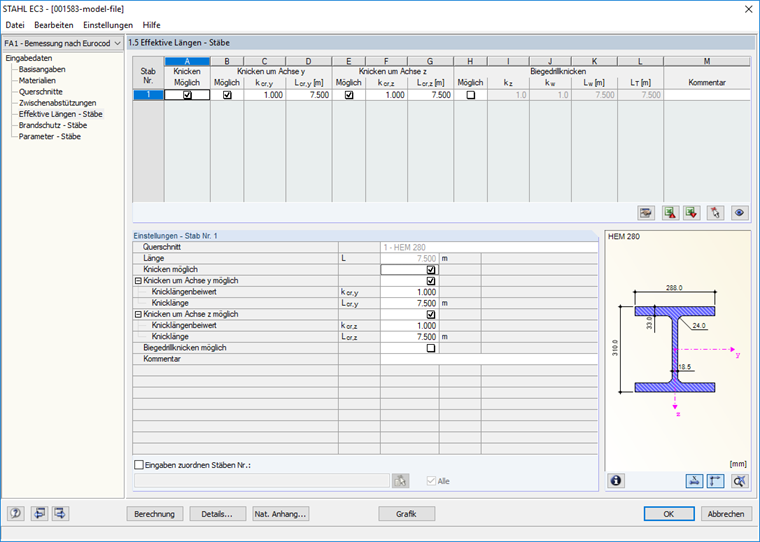
Effektive Längen - Stäbe

Biegedrillknicken wird verhindert, so dass in Maske "1.5 Effektive Längen - Stäbe" das entsprechende Kontrollkästchen deaktiviert wird (Bild 04).

4 Maske 1.5 Effektive Längen - Stäbe

Details

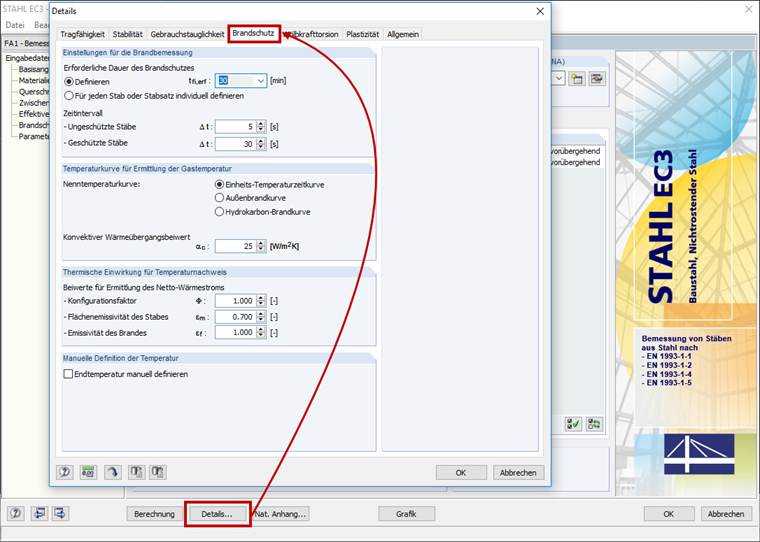
Die erforderliche Dauer des Brandschutzes, die Temperaturkurve und die Beiwerte für die Ermittlung des Netto-Wärmestroms werden im Register "Brandschutz" des Dialogs "Details" eingestellt (Bild 05).

5 Dialog Details, Register Brandschutz: Einstellungen für die Brandbemessung

Brandschutz - Stäbe

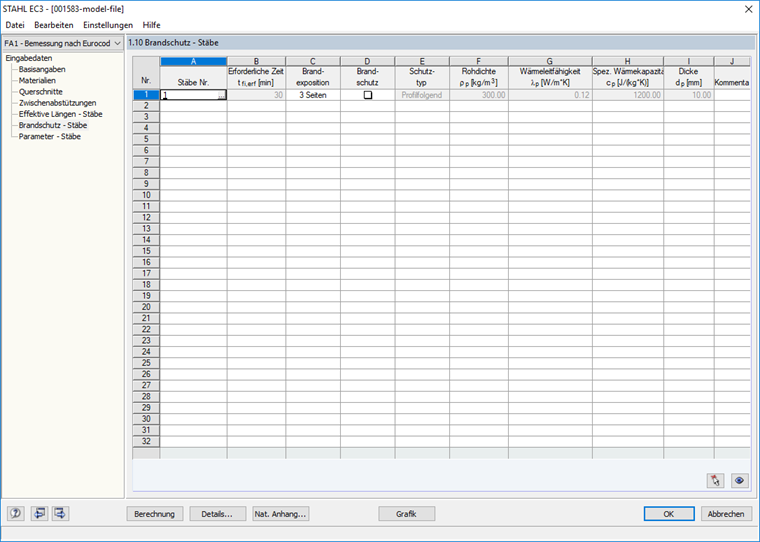
Die Brandschutzparameter wie die Brandexposition und die Brandschutzmaßnahmen sind dann in Maske "1.10 Brandschutz - Stäbe" zu definieren (Bild 06). Der ungeschützte Träger wird dreiseitig dem Brand ausgesetzt.

6 Maske 1.10 Brandschutz - Stäbe

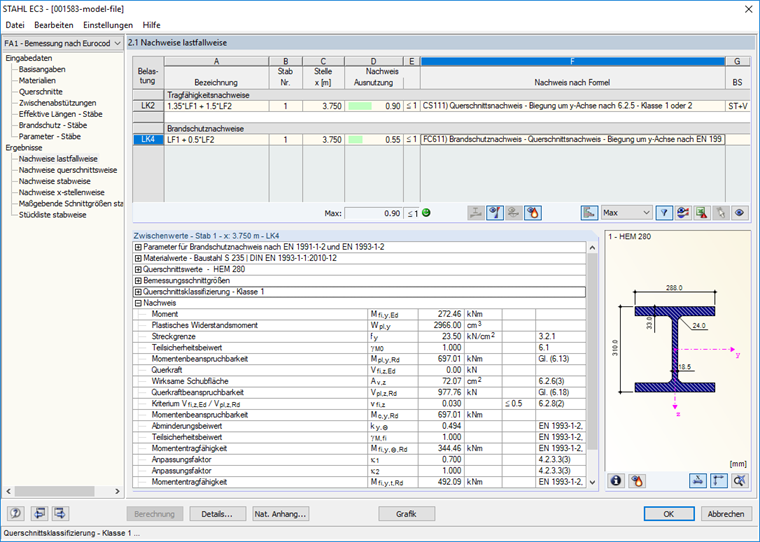
Ergebnisse

Die Ergebnisse werden nach der Berechnung angezeigt (Bild 07). Es werden auch die für die Brandbemessung relevanten Zwischenwerte wie Stahltemperatur usw. in der Tabelle "Zwischenwerte" ausgegeben.

7 Ergebnisse

Autor

Frau von Bloh bietet im Kundensupport Hilfestellung für unsere Anwender und ist zudem für die Entwicklung des Programms RSECTION sowie für den Stahl- und Aluminiumbau zuständig.

Links

Statik-Software für Stahlbau

Referenzen

Eurocode 3: Bemessung und Konstruktion von Stahlbauten − Teil 1-2: Allgemeine Regeln - Tragwerksbemessung für den Brandfall. Beuth Verlag GmbH, Berlin, 2010.
EN 1991-1-2: Eurocode 1: Einwirkungen auf Tragwerke - Teil 1-2: Allgemeine Einwirkungen - Brandeinwirkungen auf Tragwerke. Beuth Verlag GmbH, Berlin, 2002.
Mensinger, M.; Stadler, M.: Brandschutznachweise - Workshop Eurocode 3 - Rechenbeispiele. München: Technische Universität München, Lehrstuhl für Metallbau, 2008
Eurocode 3: Bemessung und Konstruktion von Stahlbauten − Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau. Beuth Verlag GmbH, Berlin, 2010

Downloads

;