16244x

001583

Sonja von Bloh, M.Sc.

2023-10-12

Kryterium odporności ogniowej zgodnie z normą DIN EN 1993-1-2

Dowód odporności ogniowej może być dostarczony w RF-/STAHL EC3 według EN 1993-1-2. Projektowanie odbywa się według uproszczonej metody obliczeniowej na poziomie nośności. Jako środki ochrony przeciwpożarowej można wybrać okładziny o różnych właściwościach fizycznych. Do wyboru są krzywa standardowa, krzywa pożaru zewnętrznego oraz krzywa pożaru węglowodorowego do określenia temperatury gazu.

Dowód ochrony przeciwpożarowej zostanie przedstawiony na przykładzie z [3].

Przykład

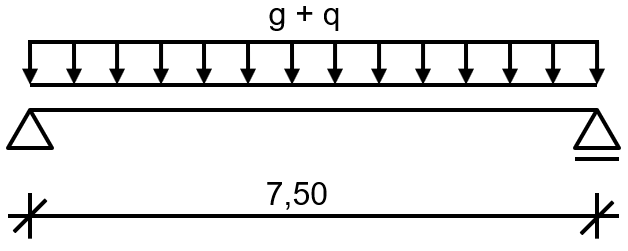
Przykład obejmuje dźwigar pomocniczy stropu pośredniego. Pas górny może być uważany za podparty bocznie w celu zapobieżenia wyboczeniu skrętnemu. Wymagana klasa odporności ogniowej wynosi R30. Układ statyczny przedstawiono na rysunku 01.

1 Układ i obciążenie

Przekrój
- HEM 280, S235, W_pl,y = 2.966 cm³
Obciążenie
- g_k = 16,25 kN/m (obciążenie stałe)
- q_k = 45,0 kN/m (obciążenie użytkowe kategoria G)

Dowód pod normalną temperaturą

Decydującą siłą jest moment w środku przęsła.

M_{y, Ed} = (γ_{G} \cdot g_{k} γ_{Q} \cdot q_{k}) \cdot \frac{l^{2}}{8}

Moment w środku rozpiętości

M_{y, Ed} = (1.35 \cdot 16.25 1.5 \cdot 45.0) \cdot \frac{7 . 50^{2}}{8} = 628.86 kNm

Obliczanie momentu w środku rozpiętości

Klasyfikacja przekroju

Klasyfikację przekroju przeprowadza się zgodnie z [4], tabela 5.2.

ε = \sqrt{\frac{235}{f_{y}}} = \sqrt{\frac{235}{235}} = 1.0

klasyfikacja przekroju

Płaszcz

\frac{c}{t} = \frac{110.8}{33} = 3.36 < 9 \cdot ε = 9 \cdot 1.0 = 9

Klasyfikacja przekroju - pas

Ściana

\frac{c}{t} = \frac{196}{18.5} = 10.59 < 72 \cdot ε = 72 \cdot 1.0 = 72

Klasyfikacja przekroju - środnik

Przekrój można przypisać do klasy 1.

Wartość obliczeniowa zdolności przenoszenia momentu

zgodnie z [4] (6.13):

M_{c, y, Rd} = M_{pl, y, Rd} = \frac{W_{pl, y} \cdot f_{y}}{γ_{M 0}} = \frac{2966 \cdot 23.5}{1.0} \cdot 10^{- 2} = 697.01 kNm

obliczeniowa nośność przy zginaniu

Dowód

Dowód zgodnie z [4] (6.12):

\frac{M_{y, Ed}}{M_{c, y, Rd}} = \frac{628.86}{697.01} = 0.90 < 1

obliczenia

Określenie temperatury stali

Wzrost temperatury w niechronionym elemencie stalowym

zgodnie z [1] (4.25):

{Δθ}_{a, t} = k_{sh} \cdot \frac{\frac{A_{m}}{V}}{c_{a} \cdot ρ_{a}} \cdot {\overset{\cdot}{h}}_{net, d} \cdot Δt

k_sh	Współczynnik poprawkowy uwzględniający efekt zacienienia
A_m/V	Współczynnik przekroju (stosunek pola powierzchni wyeksponowanej do objętości)
c_a	Ciepło właściwe
ρ_a	Gęstość stali
Δt	Interwał dla kroku czasowego
h_net,d	strumień ciepła netto

Równanie EN 1993-1-2 (4.25)

Współczynnik profilu niechronionego elementu stalowego

Współczynnik profilu wyraża stosunek niechronionej powierzchni do objętości. Współczynnik profilu jest tutaj równy obwodowi profilu stalowego pomniejszonemu o szerokość górnego kołnierza, który jest przesłonięty przez strop, w stosunku do pola przekroju.

\frac{A_{m}}{V} = \frac{U - b}{A} = \frac{1.69 - 0.288}{0.02402} = 58.368 1 / m

Współczynnik przekroju niezabezpieczonego elementu stalowego

Współczynnik profilu dla obudowy profilu

{(\frac{A_{m}}{V})}_{b} = \frac{2 \cdot h \cdot b}{A} = \frac{2 \cdot 0.310 \cdot 0.288}{0.02402} = 37.802 1 / m

Współczynnik przekroju dla przekroju zamykającego przekrój

Współczynnik korekty do uwzględnienia efektu cienia dla profilu dwuteowego

zgodnie z [1] (4.26a):

k_{sh} = 0.9 \cdot \frac{{(\frac{A_{m}}{V})}_{b}}{\frac{A_{m}}{V}} = 0.9 \cdot \frac{37.802}{58.368} = 0.583

Współczynnik poprawkowy uwzględniający efekt zacienienia dla dwuteownika

Krzywa czasowo-temperaturowa

zgodnie z [2] (3.4):

θ_{g} = 20 345 \cdot \log_{10} (8 \cdot t 1)

Standardowa krzywa temperatura-czas

Specyficzna pojemność cieplna

Dla 20 °C ≤ θ_a < 600 °C zgodnie z [1] (3.2a):

c_{a} = 425 7.73 \cdot 10^{- 1} \cdot θ_{a} - 1.69 \cdot 10^{- 3} \cdot θ_{a}^{2} 2.22 \cdot 10^{- 6} \cdot θ_{a}^{3}

Ciepło właściwe zgodnie z EN 1993-1-2 (3.2a)

Dla 600 °C ≤ θ_a < 735 °C zgodnie z [1] (3.2b):

c_{a} = 666 \frac{13002}{738 - θ_{a}}

Ciepło właściwe zgodnie z EN 1993-1-2 (3.2b)

Dla 735 °C ≤ θ_a < 900 °C zgodnie z [1] (3.2c):

c_{a} = 545 \frac{17820}{θ_{a} - 731}

Ciepło właściwe zgodnie z EN 1993-1-2 (3.2c)

Dla 900 °C ≤ θ_a ≤ 1.200 °C zgodnie z [1] (3.2d):

c_{a} = 650

Ciepło właściwe zgodnie z EN 1993-1-2 (3.2d)

Krok czasowy Δt dla metody krokowej ustala się na 5 s. Gęstość brutto stali wynosi zgodnie z [1], sekcja 3.2.2(1) ρ_a = 7.850 kg/m³.

Strumień ciepła netto

[2] (3.1)

{\overset{\cdot}{h}}_{net} = {\overset{\cdot}{h}}_{net, c} {\overset{\cdot}{h}}_{net, r}

Strumień ciepła netto zgodnie z EN 1991-1-2 (3.1)

[2] (3.2)

{\overset{\cdot}{h}}_{net, c} = α_{c} \cdot (θ_{g} - θ_{a})

α_c	Konwekcyjne współczynniki przenikania ciepła dla standardowej krzywej temperatura-czas α_c = 25 W/m²K zgodnie z [2], 3.2.1 (2)

Strumień ciepła netto zgodnie z EN 1991-1-2 (3.2)

[2] (3.3)

{\overset{\cdot}{h}}_{net, r} = Φ \cdot ε_{m} \cdot ε_{f} \cdot σ \cdot [{(θ_{g} 273)}^{4} - {(θ_{a} 273)}^{4}]

ε_m	Emisyjność powierzchni elementu konstrukcyjnego ε_m = 0,7 wg [1], 4.2.5.1(3)
ε_f	Emisyjność płomienia ε_f = 1.0 wg. z [1], 4.2.5.1(3)
σ	Stała Stephana-Boltzmanna σ = 5,67 ⋅ 10^-8 W/m² K^{4 wg.} do [2], 3.1(6)
Φ	Współczynnik konfiguracji Φ = 1,0 wg z [2], 3.1(7)

Strumień ciepła netto zgodnie z EN 1991-1-2 (3.3)

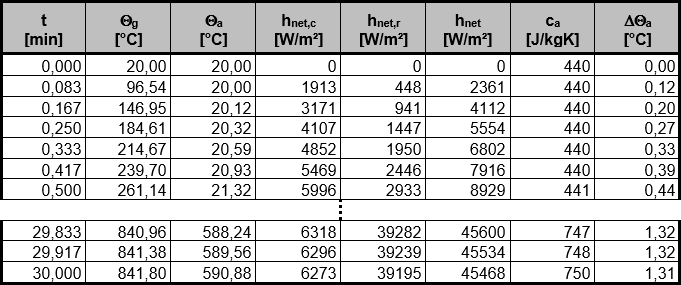
Dla temperatury stali θ_a i temperatury gazów pożarowych θ_g jako temperaturę początkową przyjmuje się temperaturę otoczenia 20 °C. Wzrost temperatury stali Δθ_a można krokowo obliczać dla każdego odcinka czasowego Δt. Temperatura stali w następnym kroku czasowym wynika z sumy temperatury stali z poprzedniego kroku i wzrostu Δθ_a. Na rysunku 02 częściowo przedstawiono przebieg rozwoju temperatury stali.

2 Rozwój temperatury stali

Decydująca temperatura stali w momencie t = 30 min wynosi tym samym θ_a = 591 °C.

Dowód w warunkach pożaru

Decydująca siła

Dla wytrzymałości pożarowej należy wziąć pod uwagę wyjątkową sytuację obliczeniową. Decydującą siłą jest moment w środku przęsła.

M_{fi, y, Ed} = (γ_{g} \cdot g_{k} \cdot ψ_{1, 1} \cdot q_{k}) \cdot \frac{l^{2}}{8} = (1.0 \cdot 16.25 \cdot 0.5 \cdot 45.0) \cdot \frac{7 . 50^{2}}{8} = 272.46 kNm

Moment w środku rozpiętości

Klasyfikacja przekroju

Klasyfikację przekroju można przeprowadzić tak samo jak pod normalną temperaturą, jednak z obniżoną wartością ε zgodnie z [1], równanie (4.2).

ε = 0.85 \cdot \sqrt{\frac{235}{f_{y}}} = 0.85 \cdot \sqrt{\frac{235}{235}} = 0.85

Wartość ε dla klasyfikacji przekroju

Płaszcz:

$\frac{c}{t} = \frac{110.8}{33} = 3.36 < 9 \cdot ε = 9 \cdot 0.85 = 7.65$

Klasyfikacja przekroju - pas
Ściana:

$\frac{c}{t} = \frac{196}{18.5} = 10.59 < 72 \cdot ε = 72 \cdot 0.85 = 61.2$

Klasyfikacja przekroju - środnik

Przekrój można przypisać do klasy 1.

Wartość obliczeniowa nośności momentu

Przy określeniu wartości obliczeniowej nośności momentu należy uwzględnić obniżenie granicy plastyczności z powodu podwyższonej temperatury. Dla temperatury stali θ_a = 591 °C współczynnik obniżenia dla granicy plastyczności interpoluje się z [1], tabela 3.1 jako:

k_{y, θ} = 0.47 \frac{(0.78 - 0.47) \cdot (591 - 600)}{(500 - 600)} = 0.498

Współczynnik redukcyjny dla granicy plastyczności

Dla niechronionego dźwigara z płytą betonową na jednej stronie i pożaru na trzech innych stronach współczynnik dostosowawczy κ₁ wynosi zgodnie z [1], 4.2.3.3(7): κ₁ = 0,7

Temperatura jest równomiernie rozłożona na długości. Daje to współczynnik dostosowawczy κ₂ zgodnie z [1], 4.2.3.3(8): κ₂ = 1,0

Wartość obliczeniową nośności momentu przy równomiernym rozkładzie temperatury określa się zgodnie z [1], 4.2.3.3 (4.8) jako:

M_{fi, y, θ, Rd} = k_{y, θ} \cdot \frac{γ_{M 0}}{γ_{M, fi}} \cdot M_{y, Rd} = 0.498 \cdot \frac{1.0}{1.0} \cdot 697.01 = 347.30 kNm

Obliczeniowa nośność przy zginaniu z równomiernym rozkładem temperatury

Wartość obliczeniową nośności momentu przy nierównomiernym rozkładzie temperatury określa się zgodnie z [1], 4.2.3.3 (4.10) jako:

M_{fi, y, t, Rd} = \frac{M_{fi, y, θ, Rd}}{κ_{1} \cdot κ_{2}}; M_{fi, y, θ, Rd} \leq M_{y, Rd}

M_{fi, y, t, Rd} = \frac{347.30}{0.7 \cdot 1.0} = 496.15 kNm

Obliczeniowa nośność przy zginaniu z nierównomiernym rozkładem temperatury

Dowód

Dowód zgodnie z [1] (4.1):

\frac{M_{fi, y, Ed}}{M_{fi, y, t, Rd}} = \frac{272.46}{496.15} = 0.55 < 1.0

Wymiarowanie EN 1993-1-2 (4.1)

RF-/STAHL EC3

Przykład obliczany jest w RF-/ STAHL EC3. Odpowiednie pliki modelu dla RFEM i RSTAB znajdują się w sekcji do pobrania na końcu artykułu.

Informacje podstawowe

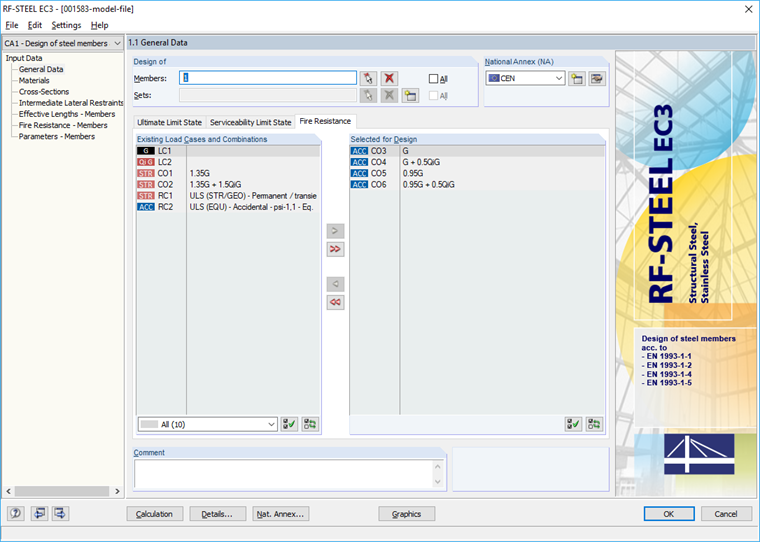
Wyznaczenie dotyczy pręta 1. Dla wyznaczenia pod normalną temperaturą w zakładce "Nośność" wybiera się kombinacje obciążeń dla sytuacji obliczeniowych stałych/przemijających zgodnie z równaniem 6.10, a dla wyznaczenia pożarowego w zakładce "Ochrona" wybiera się kombinacje obciążeń dla sytuacji obliczeniowych wyjątkowych zgodnie z równaniem 6.11c (rysunek 03).

3 Okno 1.1 Dane ogólne

Efektywne długości - pręty

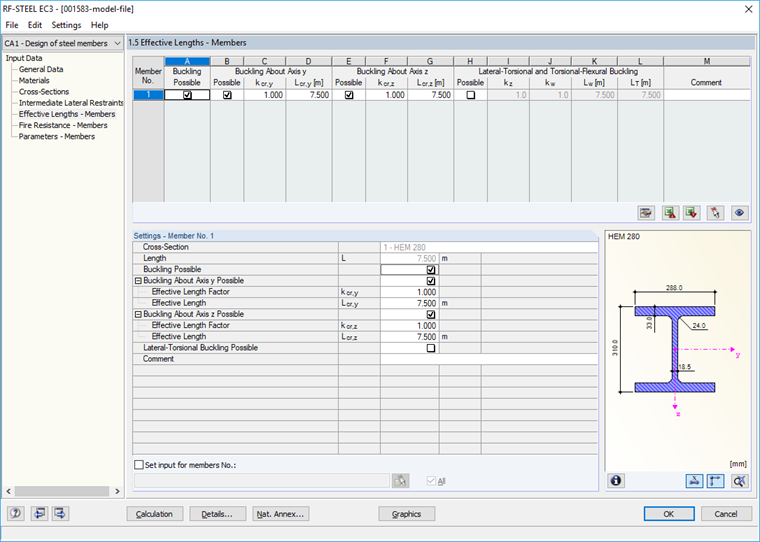
Wyboczenie skrętne zostaje zapobiegane, dlatego w masce "1.5 Efektywne długości - pręty" odpowiednie pole wyboru zostaje dezaktywowane (rysunek 04).

4 Okno 1.5 Długości efektywne - Pręty

Szczegóły

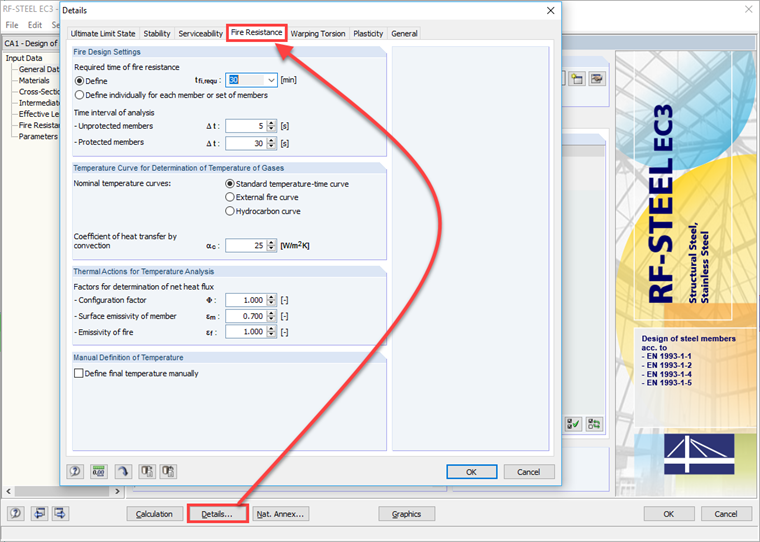
Wymagany czas trwania ochrony przeciwpożarowej, krzywa temperatury oraz współczynniki do określenia strumienia ciepła netto ustawia się w zakładce "Ochrona" w dialogu "Szczegóły" (rysunek 05).

5 Okno dialogowe Szczegóły, zakładka Odporność ogniowa: Ustawienia ognioodporności

Ochrona przeciwpożarowa - pręty

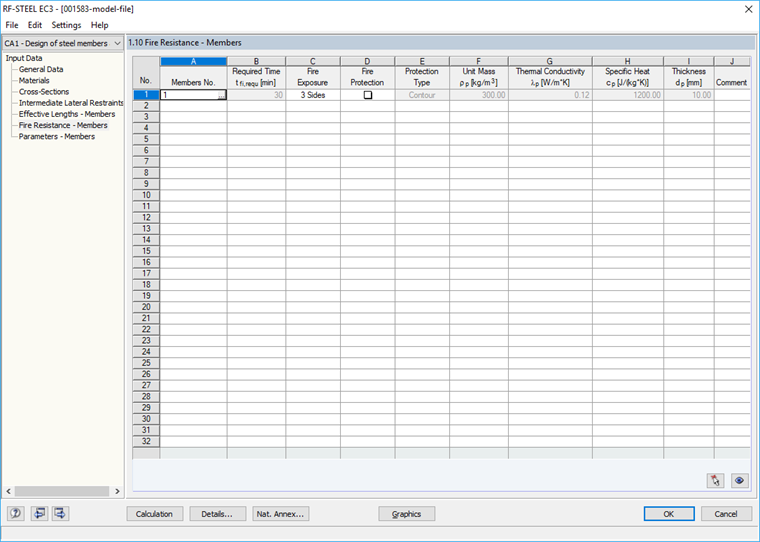
Parametry ochrony przeciwpożarowej takie jak narażenie na działanie ognia i środki ochrony przeciwpożarowej definiuje się w masce "1.10 Ochrona przeciwpożarowa - pręty" (rysunek 06). Niechroniony dźwigar jest narażony na działanie ognia z trzech stron.

6 Okno 1.10 Odporność ogniowa - Pręty

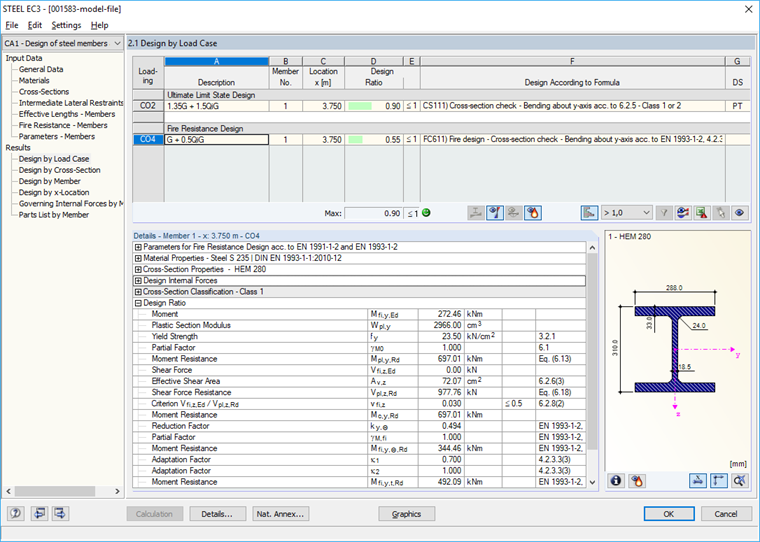
Wyniki

Wyniki są wyświetlane po zakończeniu obliczeń (rysunek 07). Podawane są również wartości pośrednie istotne dla wyznaczenia pożarowego, takie jak temperatura stali itp., w tabeli "Wartości pośrednie".

7 WYNIKI

Autor

Pani von Bloh zapewnia naszym klientom wsparcie techniczne i jest odpowiedzialna za rozwój programu SHAPE‑THIN oraz konstrukcji stalowych i aluminiowych.

Odnośniki

Oprogramowanie do analizy statyczno -wytrzymałościowej konstrukcji stalowych

Odniesienia

Eurokod 3: Projektowanie konstrukcji stalowych - Część 1-2: Allgemeine Regeln - Tragwerksbemessung für den Brandfall. Beuth Verlag GmbH, Berlin, 2010.
Europejski Komitet Normalizacyjny (2002). Eurocode 1: Einwirkungen auf Tragwerke - Teil 1-2: Allgemeine Einwirkungen - Brandeinwirkungen auf Tragwerke. Berlin: Beuth.
Mensinger, M., Stadler, M. Brandschutznachweise - Workshop Eurocode 3 - Rechenbeispiele. München: Technische Universität München, Lehrstuhl für Metallbau, 2008
Eurokod 3: Projektowanie konstrukcji stalowych - Część 1‑1: Allgemeine Bemessungsregeln und Regeln für den Hochbau. Beuth Verlag GmbH, Berlin, 2010

Pobrane

;