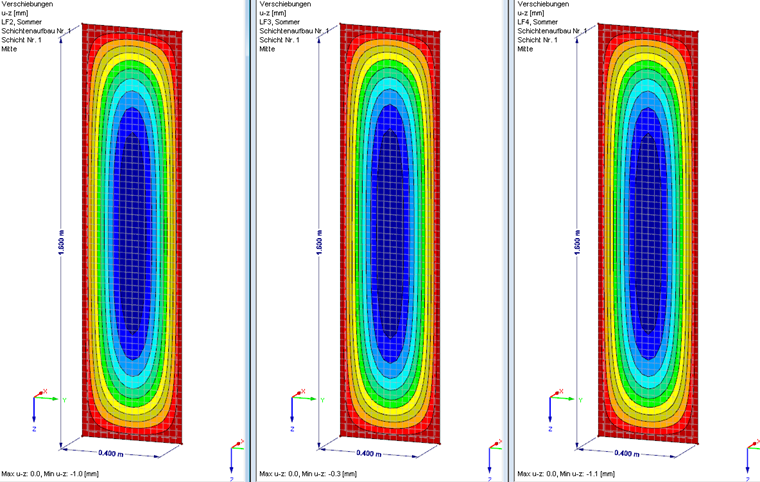
Données de base du système
Un vitrage vertical d’une hauteur de h = 1 600 mm et d’une largeur b = 400 mm est examiné. Le vitrage est supporté par des appuis encastrés sur les quatre côtés pour les charges horizontales et par des appuis ponctuels pour les charges verticales. Ce vitrage isolant à double vitrage est composé de deux vitrages de contour de 3,0 mm chacun et d’un espacement entre les vitres de 16,0 mm. L’action examinée est considérée comme le cas de charge climatique « été » conformément à DIN 18008-1 [1].
Vérification de la pression résultante du gaz
Le rapport entre la déformation et la pression résultante dans l’espace entre deux vitres peut être déterminé à l'aide de l’équation générale des gaz.
Le volume de gaz est modifié en raison des déformations calculées lors de l’analyse aux éléments finis. Si elles sont appliquées au système, on obtient les valeurs suivantes :
- Cas de charge 2, différence de température : ΔV = 645,13 cm³
- Cas de charge 3, différence de pression atmosphérique : ΔV = 186,99 cm³
- Cas de charge 4, différence d’altitude locale : ΔV = 704,16 cm³
La pression de gaz résultante peut maintenant être calculée à l’aide du volume initial et de la modification de température.
Les valeurs suivantes sont utilisées :
- p1 = 103 kN/m²
- V1 = 10 240 cm³
- T1 = 292 K
- T2 = 312 K (cas de charge 2)
- T2 = T1 = 292 K (Cas de charge 3 + 4)
Les résultats suivants sont obtenus :
- Cas de charge 2 : p2 = 103,53 kN/m²
- Cas de charge 3 : p2 = 101,15 kN/m²
- Cas de charge 4 : p2 = 96,37 kN/m²
On obtient exactement les mêmes valeurs par rapport à l’analyse EF effectuée dans RFEM.
Vérification à l’aide de la charge de surface appliquée
Lorsqu’on compare la charge appliquée sur l’ensemble du système avec un système surfacique, le plus difficile est de convertir la charge surfacique à appliquer selon DIN 18008-1 au système surfacique. De tels cas sont cependant documentés dans la littérature spécialisée ([2], par exemple), vous pouvez donc toujours y trouver des indications utiles.
Le facteur du verre isolant est calculé en fonction des dimensions du vitrage et de la structure des couches de verre. Ainsi, vous pouvez déterminer la répartition des charges dans les deux panneaux.
Les paramètres suivants sont pris en compte :
Cas de charge de différence de température
Dans le cas de charge climatique de la différence de température (été), un changement de température de 20°C est appliqué. Les pressions internes et externes sont de 1,03 bar. On obtient ainsi une charge q = 0,34 ∙ ΔT = 6,8 kN/m² et une charge s’exerçant sur le vitrage secondaire q = 6,8 ∙ 0,0754 = 0,513 kN/m².
Il est désormais possible d’effectuer une vérification « manuelle » basée sur la charge surfacique sur un vitrage simple. Cette opération ne sera cependant pas détaillée dans cet article.
Cette charge surfacique peut être utilisée pour déterminer la relation entre la charge et la pression de gaz résultante :
pextrémité,in po = 103,0 kN/m² + 0,513 kN/m² = 103,513 kN/m²
Cas de charge de la différence de pression atmosphérique
La différence de pression atmosphérique est spécifiée par une différence de pression de 0,02 bar. On obtient ainsi une charge q = 103,0 − 101,0 = 2,0 kN/m² sur l’ensemble du système. La charge sur un vitrage simple avec les mêmes dimensions est donc q = 2,0 ∙ 0,0754 = 0,151 kN/m².
La pression du gaz résultante dans l’espace entre les vitres résulte également de la somme de la pression finale et de la charge de surface appliquée :
pextrémité,in po = 101,0 kN/m² + 0,151 kN/m² = 101,151 kN/m²
Cas de charge de la différence d’altitude
Dans le cas de charge de la différence d’altitude, la différence d’altitude locale de 600 m est appliquée par défaut. La charge résultante est ainsi calculée comme suit : q = 0,012 ∙ 600 = 7,2 kN/m². Celle-ci est convertie pour le système unique comme suit : q = 7,2 ∙ 0,0754 = 0,543 kN/m².
En supposant que la pression atmosphérique sur le site d’installation est d’environ 7,2 kN/m² inférieure à celle sur le site de production, la pression de gaz résultante dans l’espace entre les vitres peut également être calculée comme suit :
pend,in = (103.0 kN/m² - 7.2 kN/m²) + 0,543 = 96,343 kN/m²
Conclusion
Le calcul comparatif a montré que les résultats du calcul non linéaire aux éléments finis sont très similaires à ceux du calcul à l’aide de formules analytiques. La procédure décrite montre une simple vérification du calcul global assisté par ordinateur. De plus, cet article a essayé de clarifier les relations entre les charges sur le vitrage et les conditions de pression dans l’espace entre les vitrages.
Vous pouvez également vérifier les déformations et les contraintes à l’aide des charges calculées ci-dessus. Dans ce cas, il convient de noter que le calcul informatique est généralement basé sur l’analyse non linéaire des grandes déformations, dans laquelle les formules analytiques ont été développées selon l’analyse statique linéaire. Les résultats peuvent donc présenter de légères différences.