Онлайновые руководства Фоновое знание RFEM 6

Назад к руководствам онлайн

540x

004088

2023-09-28

Выбрать руководство

Обзор

Введение

Вычисление

Конечные элементы

Нелинейность материала

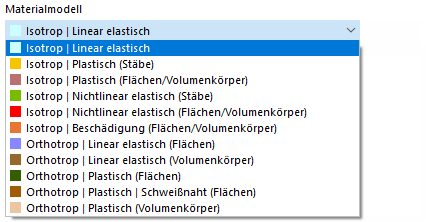
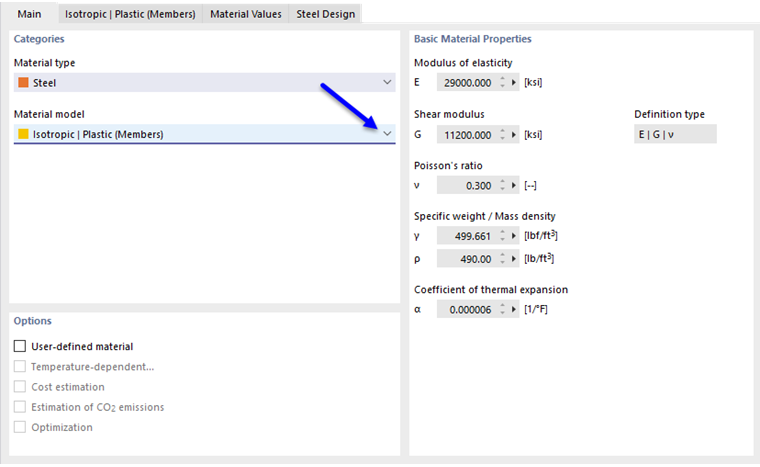
Если в "Модель - Основные данные" активирован дополнительный модуль анализа нелинейного поведения материала (необходима лицензия), в списке моделей материалов будут доступны дополнительные опции выбора, кроме моделей материалов "Изотропный | Линейно упругий" и "Ортотропный | Линейно упругий".

Модели материалов для аддона анализа "Нелинейное поведение материалов"

Модели материалов для аддона Анализ нелинейных материалов

Если вы используете нелинейные модели материалов в RFEM, всегда выполняется итеративный расчет. В зависимости от модели материала определяется иная зависимость между напряжениями и деформациями.

Жесткость конечно-элементных структур постоянно корректируется в процессе итераций до тех пор, пока не будет достигнута зависимость напряжение-деформация. Корректировка всегда проводится для всей поверхности или объемного элемента. Поэтому рекомендуется всегда использовать тип сглаживания "Постоянный на элементах сетки" при оценке напряжений.

Сглаживание результатов

Некоторые модели материалов в RFEM обозначаются как "Пластичный", другие как "Нелинейно упругий".

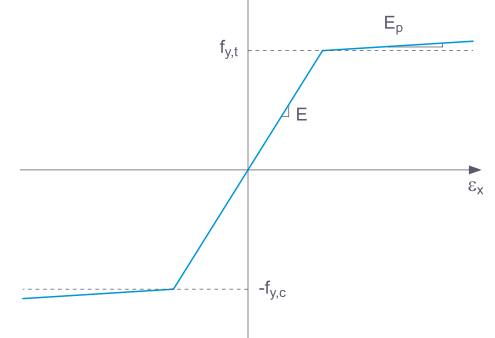
Если компонент конструкции с нелинейно упругим материалом снова освободится, деформация возвращается по тому же пути. При полном разгрузке деформации не остается.

Диаграмма напряжение-деформация, нелинейно-упругая

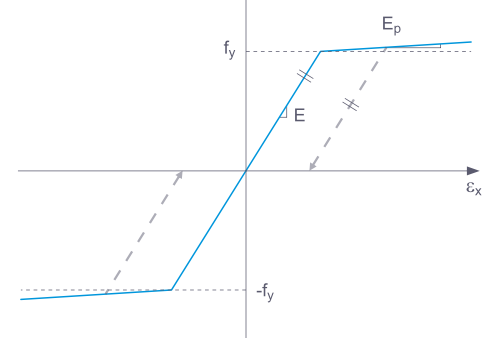
При разгрузке компонента конструкции с Пластичной моделью материала деформация сохраняется после полной разгрузки.

Диаграмма напряжение-деформация, пластическая

Фоновая информация о нелинейных моделях материалов доступна в технической статье, описывающей Законы течения в изотропной нелинейной упругой модели материала.

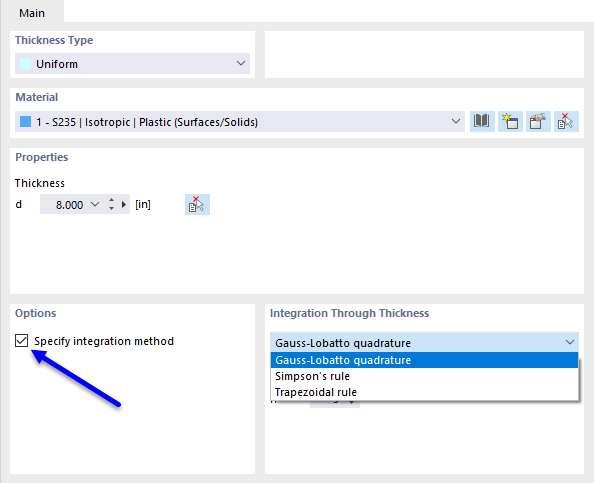
Внутренние усилия и моменты в пластинах с нелинейным материалом получаются путем численной интеграции напряжений по толщине d пластины. Чтобы определить метод интеграции для толщины, выберите опцию "Указать метод интеграции" в диалоговом окне "Редактировать толщину". Доступны следующие методы интеграции:

Квадратура Гаусса-Лобатто
Правило Симпсона
Правило трапеций

Определить метод интегрирования для толщины поверхности

Кроме того, вы можете указать "Количество точек интеграции" от 3 до 99 по толщине пластины.

Инфо

Теоретическое объяснение отдельных методов интеграции можно найти в Многослойные поверхности онлайн-руководстве.

Изотропный Пластичный | Стержни)

При выборе записи Изотропный | Пластичный (Стержни) в выпадающем списке "Модель материала", вкладка для ввода нелинейных параметров материала становится доступной.

Активация нелинейной модели материала

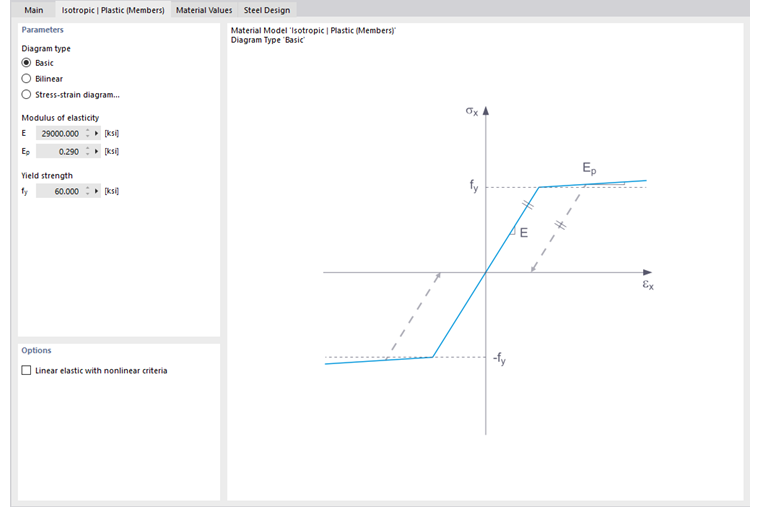
Определение нелинейных параметров материала

На этой вкладке вы определяете диаграмму напряжение-деформация. Доступны следующие опции:

Основной
Билинейный
Диаграмма напряжение-деформация

Если выбран Основной, RFEM использует билинейную модель материала. Значения из базы данных материалов используются для модуля упругости E и предела текучести f_y. По числовым причинам ветвь графика не точно горизонтальна, а имеет небольшой уклон E_p.

Если вы хотите изменить значения для предела текучести и модуля упругости, активируйте флажок "Пользовательский материал" на вкладке "Основные".

Активировать пользовательский материал

Для билинейного определения также можно ввести значение для E_p.

Более сложные зависимости между напряжением и деформацией можно определить с помощью "Диаграммы напряжение-деформация". При выборе этой опции отображается вкладка "Диаграмма напряжение-деформация".

Ввод пользовательской диаграммы напряжение-деформация

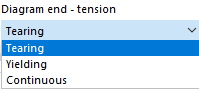
Определите точку для зависимости напряжение-деформация в каждой строке таблицы. Вы можете выбрать, как диаграмма продолжается после последней точки в списке "Конец диаграммы" под диаграммой:

Плавный переход от последней точки определения

Переход после последней точки определения

В случае "Рассечение", напряжение после последней точки определения возвращается к нулю. "Текучесть" означает, что напряжение остается постоянным при увеличении деформации. "Непрерывность" означает, что график продолжается с наклоном последнего участка.

Инфо

В этой модели материала диаграмма напряжение-деформация относится к продольному напряжению σ_x. Разные пределы текучести для растяжения и сжатия не могут быть учтены этой моделью материала.

Изотропный Пластичный | Поверхности/Твердые тела

При выборе записи "Изотропный | Пластичный (Поверхности/Твердые тела)" в выпадающем списке "Модель материала", вкладка для ввода нелинейных параметров материала становится доступной.

Выберите модель пластического материала

Сначала выберите "Гипотезу разрушения напряжений". Доступны следующие гипотезы для выбора:

фон Мизеса (критерий текучести фон Мизеса)
Треска (критерий текучести Треска)
Друкер-Прагер
Мора-Кулон

Определение гипотезы разрушения при напряжении

При выборе "фон Мизеса" на диаграмме напряжение-деформация используется следующее напряжение:

Поверхности:

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{xy}^{2})}

Эквивалентное напряжение из основных напряжений по фон Мизесу

Твердые тела:

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Эквивалентное напряжение σ_{v, Мизес} от основных напряжений

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Эквивалентное напряжение σ_{v, Мизес} от главных напряжений

Согласно гипотезе "Треска", используется следующее напряжение:

Поверхности:

σ_{v} = \sqrt{{(σ_{x} - σ_{y})}^{2} + 4 {τ_{xy}}^{2}}

Эквивалентное напряжение по Треске

Твердые тела:

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Эквивалентное напряжение σ_{v, Tresca}

Согласно гипотезе "Друкер-Прагер", для поверхностей и твердых тел используется следующее напряжение:

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}

m = \frac{σ_{c}}{σ_{t}}

σ_c	Пограничное напряжение для сжатия
σ_t	Предел прочности при растяжении

Критерий текучести по Друкеру-Прагеру

Согласно гипотезе "Мора-Кулон", для поверхностей и твердых тел используется следующее напряжение:

σ_{v} = \frac{m + 1}{2} \max \{|σ_{1} - σ_{2}| + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}| + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}| + K (σ_{3} + σ_{1})\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

Мор - Кулон

Изотропный Нелинейно Упругий | Стержни

Функциональность в значительной степени соответствует модели материала изотропный пластичный (стержни). Разница в том, что после разгрузки не остается пластических деформаций.

Изотропный Нелинейно Упругий | Поверхности/Твердые тела

Функциональность в значительной степени соответствует модели материала изотропный пластичный (поверхности/твердые тела). Разница в том, что после разгрузки не остается пластических деформаций.

Изотропное Повреждение | Поверхности/Твердые тела

В отличие от других моделей материалов, диаграмма напряжение-деформация для этой модели материала не антиметрична относительно начала координат. Например, поведение бетона с добавлением стальных волокон можно отображать с этой моделью материала. Подробную информацию о моделировании бетона с добавлением стальных волокон можно найти в технической статье о Определении свойств материала бетона, армированного стальными волокнами.

Модель материала «Изотропная | Ущерб »

В этой модели материала изотропная жесткость уменьшается с помощью скалярного параметра повреждения. Этот параметр повреждения определяется из кривой напряжения, заданной в диаграмме. Это не учитывает направление главных напряжений; вместо этого повреждение происходит в направлении эквивалентной деформации, которая также охватывает третье направление, перпендикулярное плоскости. Область напряжений и сжатия тензора напряжений обрабатывается отдельно. В каждом случае применяются разные параметры повреждения.

"Размер элемента эталона" контролирует, как деформация в области трещины масштабируется к длине элемента. При значении по умолчанию, равном нулю, масштабирование не выполняется. Таким образом, поведение материала бетона с добавлением стальных волокон моделируется реалистично.

Более подробную информацию о теоретическом фоне модели материала "Изотропное повреждение" можно найти в технической статье, описывающей Модель нелинейного материала Повреждение.

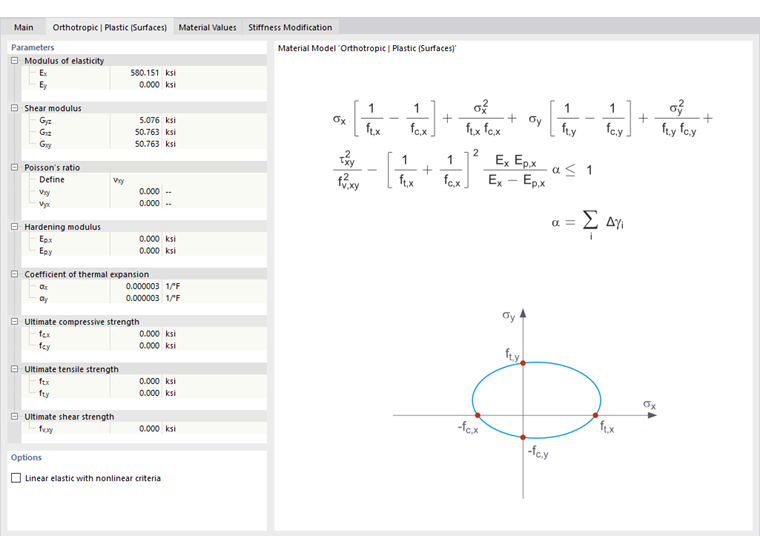
Ортотропный Пластичный | Поверхности/Твердые тела

Модель материала по "Цаи-Ву" объединяет пластичность с ортотропными свойствами. Это позволяет специальное моделирование материалов с анизотропными характеристиками, таких как пластмассы, армированные волокном, или древесина.

Если материал пластичен, напряжения остаются постоянными. Перераспределение осуществляется в соответствии с жесткостями, доступными в отдельных направлениях.

Модель материала «Ортотропная | Пластик (поверхности) »

Модель материала ' ортотропная | Пластик (сплошной) '

Упругая область соответствует модели материала Ортотропный. Следующее условие текучести по Цаи-Ву применяется к пластичной зоне:

Поверхности (2D):

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

\frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} - {[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Цай-Ву, Планарное напряженное состояние

Твердые тела (3D):

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

σ_{z} [\frac{1}{f_{t, z}} - \frac{1}{f_{c, z}}] + \frac{{σ_{z}}^{2}}{f_{t, z} f_{c, z}} +

\frac{{τ_{yz}}^{2}}{{f_{v, yz}}^{2}} + \frac{{τ_{xz}}^{2}}{{f_{v, xz}}^{2}} + \frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} -

{[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Цай-Ву, Пространственное напряжение

Все прочности должны быть определены положительно.

Вы можете рассматривать критерий напряжения как эллиптическую поверхность в шестеростновом пространстве напряжений. Если один из трех компонентов напряжения используется как постоянное значение, поверхность может быть спроецирована на трехмерное пространство напряжений.

Если значение для f_y(σ) согласно уравнению Цаи-Ву, условие плоского напряжения, меньше 1, то напряжения находятся в упругой зоне. Пластическая зона достигается, как только f_y(σ) = 1. Значения выше 1 недопустимы. Поведение модели является идеально-пластичным, что означает отсутствие упрочнения.

Исходная глава

Нелинейность