Instrukcje online Podstawowe informacje o RFEM 6

Powrót do Instrukcji online

540x

004088

2023-09-28

Wybór ręczny

Przegląd

Wprowadzenie

Obliczenia

Elementy skończone

Nieliniowość materiałowa

Jeśli w Model - Dane Podstawowe aktywowano dodatek do analizy nieliniowego zachowania materiału (wymagana licencja), to na liście modeli materiałowych dostępne są dodatkowe opcje wyboru oprócz modeli materiałowych "Izotropowy | Liniowy sprężysty" i "Ortotropowy | Liniowy sprężysty".

Modele materiałowe dla addonu Analiza nieliniowego zachowania materiałów

Modele materiału do dodatku Analiza nieliniowego zachowania materiałów

Jeśli używasz nieliniowych modeli materiałowych w RFEM, zawsze wykonywane są obliczenia iteracyjne. W zależności od modelu materiału definiowana jest różna relacja między naprężeniami a odkształceniami.

Sztywność elementów skończonych jest w trakcie iteracji wielokrotnie dostosowywana, aż zostanie spełniona relacja naprężenie-odkształcenie. Dostosowanie jest zawsze przeprowadzane dla całej powierzchni lub elementu stałego. Dlatego zalecamy zawsze używać typu wygładzania "Stały" na elementach siatki przy ocenie naprężeń.

Uśrednianie wyników

Niektóre modele materiałowe w RFEM są oznaczone jako "Plastyczne", inne jako "Nieliniowo sprężyste".

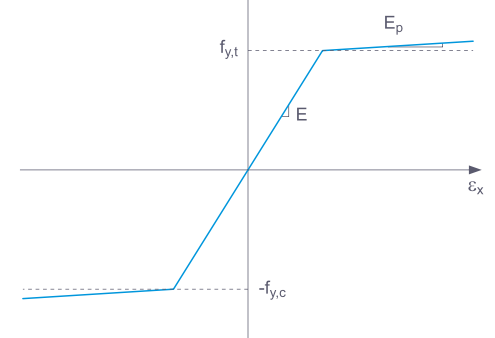
Jeśli element konstrukcyjny z materiałem nieliniowo sprężystym jest odciążony, odkształcenie wraca tą samą ścieżką. Po całkowitym odciążeniu nie pozostaje żadne odkształcenie.

Wykres naprężenie-odkształcenie, nieliniowy wykres sprężysty

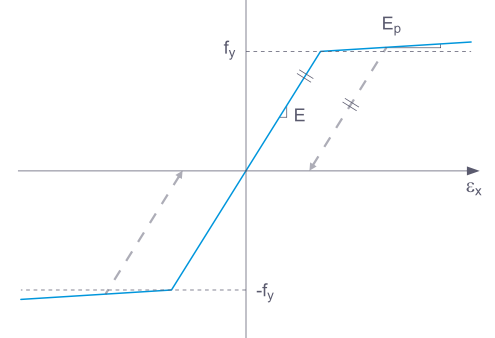
Podczas odciążania elementu konstrukcyjnego z modelem materiału Plastycznym odkształcenie pozostaje po całkowitym odciążeniu.

Wykres naprężenie-odkształcenie, tworzywo sztuczne

Informacje w tle na temat nieliniowych modeli materiałowych można znaleźć w artykule technicznym opisującym Prawa plastyczności w izotropowym nieliniowym modelu materiału sprężystego.

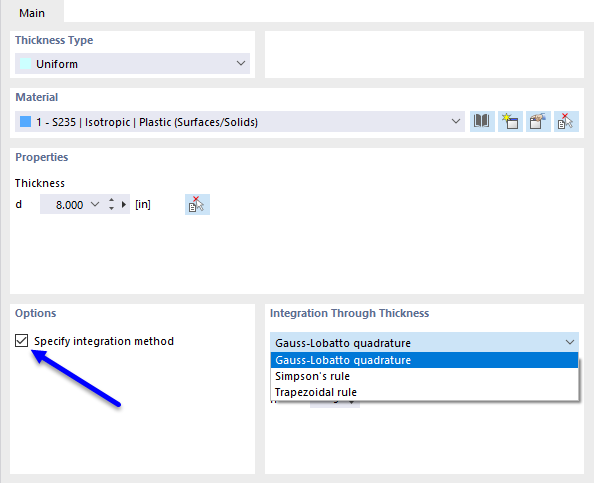
Siły wewnętrzne i momenty w płytach z materiałów nieliniowych wynikają z numerycznej integracji naprężeń po grubości d płyty. Aby zdefiniować metodę integracji dla grubości, wybierz opcję "Określ metodę integracji" w oknie dialogowym "Edytuj grubość". Dostępne są następujące metody integracji:

Kwadratura Gaussa-Lobatto
Reguła Simpsona
Reguła trapezów

Zdefiniuj metodę całkowania dla grubości powierzchni

Ponadto możesz określić "Liczbę punktów integracji" od 3 do 99 przez grubość płyty.

Informacje

Teoretyczne wyjaśnienie poszczególnych metod integracji można znaleźć w Wielowarstwowe powierzchnie podręczniku online.

Izotropowy plastyczny | Pręty

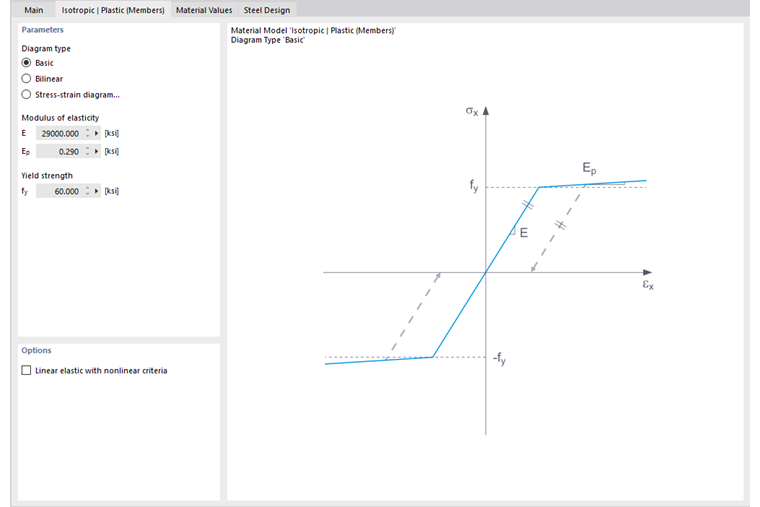
Wybór wpisu Izotropowy | Plastyczny (Pręty) na liście rozwijanej "Model materiału" umożliwia zakładkę do wprowadzania nieliniowych parametrów materiałowych.

Aktywacja nieliniowego modelu materiałowego

Zdefiniuj nieliniowe parametry materiałowe

W tej zakładce definiujesz wykres naprężenie-odkształcenie. Dostępne są następujące opcje:

Podstawowy
Biliniowy
Diagram naprężenie-odkształcenie

Jeśli wybrano Podstawowy, RFEM używa biliniowego modelu materiałowego. Wartości z bazy danych materiałowych są używane w przypadku modułu sprężystości E i granicy plastyczności f_y Ze względów numerycznych, gałąź wykresu nie jest dokładnie pozioma, lecz ma małe nachylenie E_p.

Jeśli chcesz zmienić wartości granicy plastyczności i modułu sprężystości, aktywuj pole wyboru "Materiał użytkownika" w zakładce "Główna".

Aktywuj materiał zdefiniowany przez użytkownika

Dla definicji biliniowej można również wprowadzić wartość E_p.

Bardziej złożone relacje pomiędzy naprężeniem a odkształceniem mogą być definiowane za pomocą "Diagramu naprężenie-odkształcenie". Wybór tej opcji powoduje wyświetlenie zakładki "Diagram naprężenie-odkształcenie".

Wprowadź zdefiniowany przez użytkownika wykres naprężenie-odkształcenie

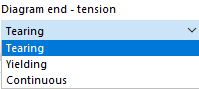
Zdefiniuj punkt dla relacji naprężenie-odkształcenie w każdym wierszu tabeli. Możesz wybrać, jak wykres kontynuuje się po ostatnim punkcie definicji na liście "Koniec diagramu" poniżej wykresu:

Rozkład według ostatniego punktu definicji

W przypadku "Tearing", naprężenie po ostatnim punkcie definicji spada do zera. "Plastyfikacja" oznacza, że naprężenie pozostaje stałe, gdy odkształcenie rośnie. "Ciągły" oznacza, że wykres kontynuuje się z nachyleniem ostatniego odcinka.

Informacje

W tym modelu materiału diagram naprężenie-odkształcenie odnosi się do naprężenia wzdłużnego σ_x. Różne wytrzymałości na rozciąganie i ściskanie nie są uwzględniane przez ten model materiałowy.

Izotropowy plastyczny | Powierzchnie/Stałe

Wybór wpisu "Izotropowy | Plastyczny (Powierzchnie/Stałe)" na liście rozwijanej "Model materiału" umożliwia zakładkę do wprowadzania nieliniowych parametrów materiałowych.

Wybierz model z tworzywa sztucznego

Najpierw wybierz "Hipotezę zniszczenia naprężenia". Dostępne są następujące hipotezy do wyboru:

von Mises (kryterium plastyczności von Misesa)
Tresca (kryterium plastyczności Tresca)
Drucker-Prager
Mohr-Coulomb

Zdefiniuj hipotezę uszkodzenia naprężeniowego

Wybierając "von Mises", jest używane następujące naprężenie w diagramie naprężenie-odkształcenie:

Powierzchnie:

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{xy}^{2})}

Naprężenia równoważne z naprężeń podstawowych według von Misesa

Stałe:

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Naprężenie równoważne σ_v,Mises z naprężeń podstawowych

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Naprężenie równoważne σ_{v, Mises} z naprężeń głównych

Według hipotezy "Tresca", jest używane następujące naprężenie:

Powierzchnie:

σ_{v} = \sqrt{{(σ_{x} - σ_{y})}^{2} + 4 {τ_{xy}}^{2}}

Naprężenie równoważne według Tresca

Stałe:

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Naprężenie równoważne σ_{v, Tresca}

Według hipotezy "Drucker-Prager", jest używane następujące naprężenie dla powierzchni i stałych:

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}

m = \frac{σ_{c}}{σ_{t}}

σ_c	Naprężenie graniczne w ściskaniu
σ_t	Naprężenie graniczne dla rozciąganie

Kryterium wydajności według Druckera-Pragera

Według hipotezy "Mohr-Coulomb", jest używane następujące naprężenie dla powierzchni i stałych:

σ_{v} = \frac{m + 1}{2} \max \{|σ_{1} - σ_{2}| + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}| + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}| + K (σ_{3} + σ_{1})\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

Mohr-Coulomb

Izotropowy nieliniowy sprężysty | Pręty

Funkcjonalność w dużej mierze odpowiada funkcjonalności izotropowego modelu materiałowego plastycznego (pręty). Różnica polega na tym, że po odciążeniu nie pozostaje żadne odkształcenie plastyczne.

Izotropowy nieliniowy sprężysty | Powierzchnie/Stałe

Funkcjonalność w dużej mierze odpowiada funkcjonalności izotropowego modelu materiałowego plastycznego (powierzchnie/stałe). Różnica polega na tym, że po odciążeniu nie pozostaje żadne odkształcenie plastyczne.

Izotropowe zniszczenie | Powierzchnie/Stałe

W przeciwieństwie do innych modeli materiałowych, diagram naprężenie-odkształcenie dla tego modelu materiału nie jest antysymetryczny do początku układu. Tak więc, zachowanie betonu zbrojonego włóknami stalowymi można przedstawić za pomocą tego modelu materiału, na przykład. Szczegółowe informacje na temat modelowania betonu zbrojonego włóknami stalowymi można znaleźć w artykule technicznym o Określanie właściwości materiałowych betonu zbrojonego włóknami stalowymi.

Model materiałowy „Izotropowy | Uszkodzenia"

W tym modelu materiałowym izotropowa sztywność jest redukowana za pomocą skalarowego parametru uszkodzenia. Ten parametr uszkodzenia jest wyznaczany na podstawie krzywej naprężenia zdefiniowanej w Diagramie. Nie uwzględnia to kierunku naprężeń głównych; raczej, uszkodzenie występuje w kierunku równoważnego odkształcenia, które obejmuje również trzeci kierunek prostopadły do płaszczyzny. Obszar naprężenia na rozciąganie i ściskanie tensora naprężeń jest traktowany oddzielnie. Różne parametry uszkodzenia mają zastosowanie w każdym przypadku.

"Wielkość referencyjna elementu" kontroluje, jak odkształcenie w obszarze pęknięcia jest skalowane do długości elementu. Przy wartości domyślnej wynoszącej zero, nie wykonuje się skalowania. Tak więc, zachowanie materiału betonu zbrojonego włóknami stalowymi jest modelowane realistycznie.

Więcej informacji na temat teoretycznego tła modelu materiałowego "Izotropowe zniszczenie" można znaleźć w artykule technicznym opisującym Nieliniowy model materiałowy uszkodzenia.

Ortotropowy plastyczny | Powierzchnie/Stałe

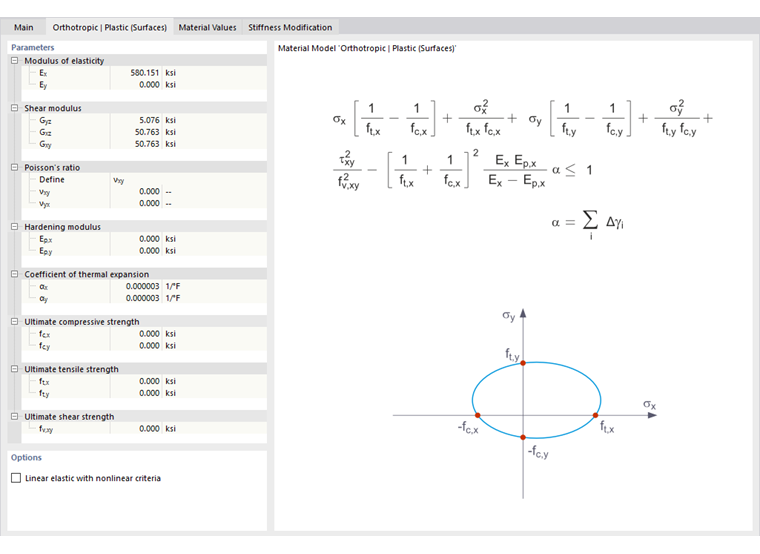
Model materiału według "Tsai-Wu" łączy właściwości plastyczne z ortotropowymi. Pozwala to na specjalne modelowanie materiałów o charakterystyce anizotropowej, takich jak plastiki wzmacniane włóknami lub drewno.

Jeśli materiał jest uplastyczniony, naprężenia pozostają stałe. Redystrybucja jest przeprowadzana zgodnie z dostępnością sztywności w poszczególnych kierunkach.

Model materiałowy „Ortotropowy | Plastik (powierzchnie)"

Model materiałowy ' ortotropowy | Plastyczny (brył) '

Obszar sprężysty odpowiada modelowi materiałowemu ortotropowemu. Następujące warunki plastyczności według Tsai-Wu dotyczą strefy plastycznej:

Powierzchnie (2D):

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

\frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} - {[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu, płaski stan naprężenia

Stałe (3D):

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

σ_{z} [\frac{1}{f_{t, z}} - \frac{1}{f_{c, z}}] + \frac{{σ_{z}}^{2}}{f_{t, z} f_{c, z}} +

\frac{{τ_{yz}}^{2}}{{f_{v, yz}}^{2}} + \frac{{τ_{xz}}^{2}}{{f_{v, xz}}^{2}} + \frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} -

{[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu, Przestrzenny stan naprężeń

Wszystkie wytrzymałości muszą być zdefiniowane jako dodatnie.

Można uważać kryterium naprężeń za eliptyczną powierzchnię w sześciowymiarowej przestrzeni naprężeń. Jeśli jedna z trzech składowych naprężeń jest podana jako wartość stała, powierzchnia może być rzutowana na trójwymiarową przestrzeń naprężeń.

Jeśli wartość f_y(σ) według równania Tsai-Wu, warunek stanu naprężeń płaskich, jest mniejsza niż 1, naprężenia znajdują się w strefie sprężystej. Strefa plastyczna jest osiągana, gdy f_y(σ) = 1. Wartości wyższe niż 1 nie są dozwolone. Zachowanie modelu jest idealnie-plastyczne, co oznacza, że nie występuje usztywnienie.

Rozdział nadrzędny

Nieliniowość