Manuels en ligne Connaissances de base sur RFEM 6

Retour aux manuels en ligne

540x

004088

28.09.2023

Sélectionner le Manuel

Aperçu

Introduction

Calcul de déformation

Éléments finis

Non-linéarité du matériau

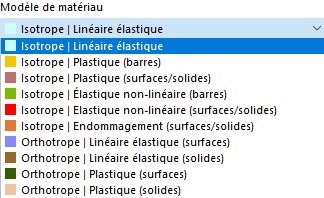
Si l'extension d'analyse du Comportement Non Linéaire des Matériaux est activée (licence requise) dans le Modèle - Données de base, des options supplémentaires de sélection apparaissent dans la liste des modèles de matériau en plus des modèles "Isotrope | Elasticité Linéaire" et "Orthotrope | Elasticité Linéaire".

Modèle de matériau pour le module complémentaire Comportement non linéaire du matériau

Si vous utilisez des modèles de matériau non linéaires dans RFEM, un calcul itératif est toujours effectué. Selon le modèle de matériau, une relation différente entre les contraintes et les déformations est définie.

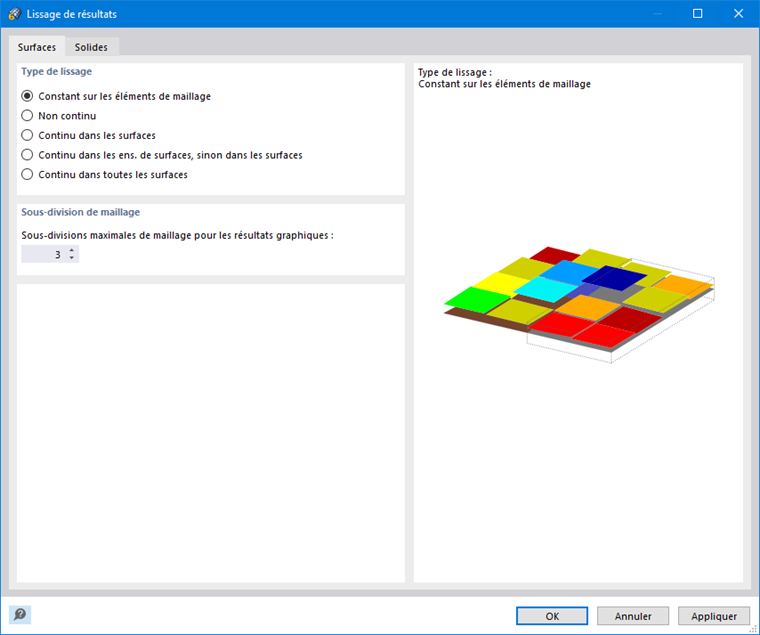
La raideur des éléments finis est ajustée continuellement au cours des itérations jusqu'à ce que la relation contrainte-déformation soit satisfaite. L'ajustement est toujours effectué pour une surface ou un élément solide entier. Par conséquent, nous recommandons d'utiliser toujours le type de lissage Constant sur les éléments de maillage lors de l'évaluation des contraintes.

Lissage de résultats

Certains modèles de matériau dans RFEM sont indiqués par "Plastique", d'autres par "Non Linéaire Élastique".

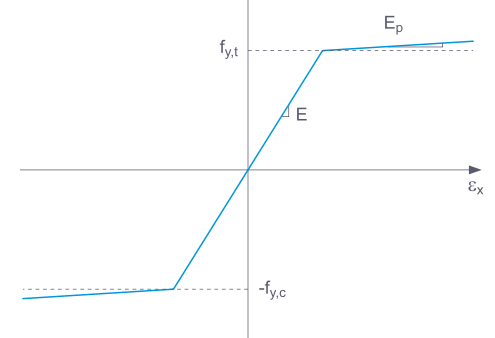
Si un composant structurel avec un matériau non linéaire élastique est de nouveau libéré, la déformation revient par le même chemin. Lorsqu'il est complètement déchargé, aucune déformation ne reste.

Diagramme contrainte-déformation, élastique non linéaire

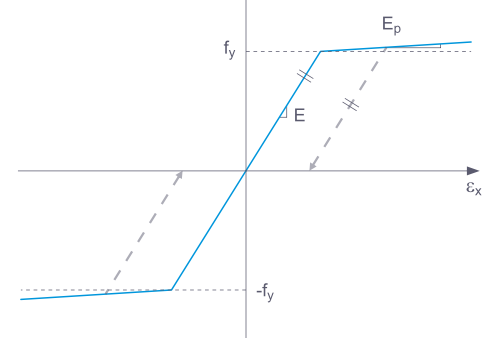
Lors de la décharge d'un composant structurel avec un modèle de matériau Plastique, la déformation reste après qu'il a été complètement déchargé.

Diagramme contrainte-déformation plastique

Des informations de fond sur les modèles de matériau non linéaire peuvent être trouvées dans l'article technique décrivant les Lois de plastification dans le modèle de matériau isotrope non linéaire élastique.

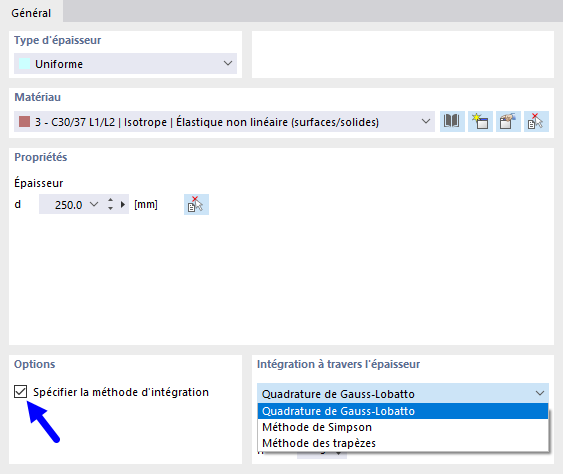
Les forces internes et les moments dans les plaques avec matériau non linéaire résultent de l'intégration numérique des contraintes sur l'épaisseur d de la plaque. Pour définir la méthode d'intégration pour l'épaisseur, sélectionnez l'option Spécifier la méthode d'intégration dans la boîte de dialogue "Éditer l'épaisseur". Les méthodes d'intégration suivantes sont disponibles :

Quadrature de Gauss-Lobatto
Règle de Simpson
Règle trapézoïdale

Définir la méthode d’intégration pour l’épaisseur de surface

De plus, vous pouvez spécifier le "Nombre de points d'intégration" de 3 à 99 en fonction de l'épaisseur de la plaque.

Informations

Une explication théorique des méthodes d'intégration individuelles peut être trouvée dans le manuel en ligne Surfaces Multicouches.

Isotrope Plastique | Barres)

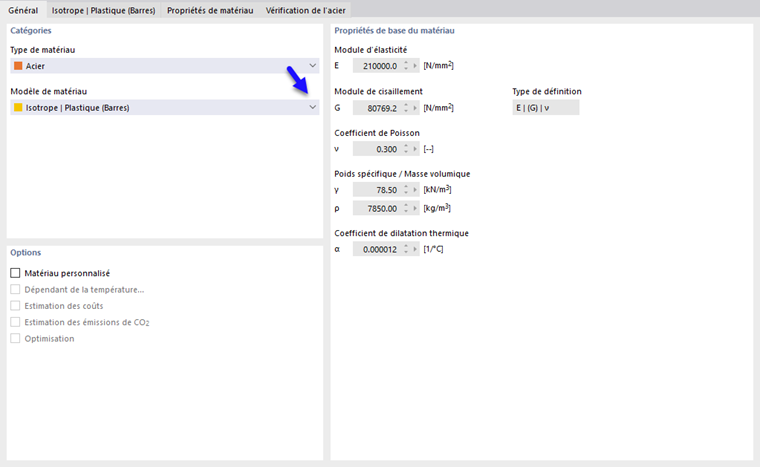
En sélectionnant l'entrée Isotrope | Plastique (Barres) dans la liste déroulante "Modèle de matériau", l'onglet pour entrer les paramètres de matériau non linéaire est activé.

Activer le modèle de matériau non linéaire

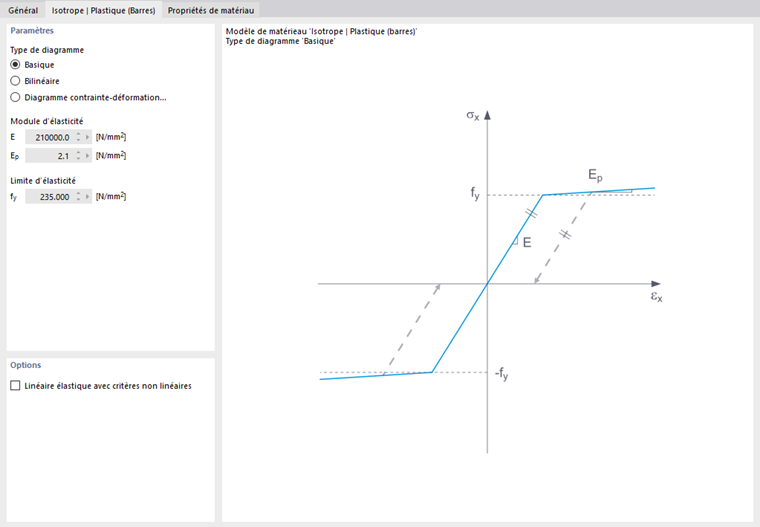
Définir les paramètres de matériau non linéaire

Dans cet onglet, vous définissez le diagramme contrainte-déformation. Les options suivantes sont disponibles :

Basique
Bilinéaire
Diagramme contrainte-déformation

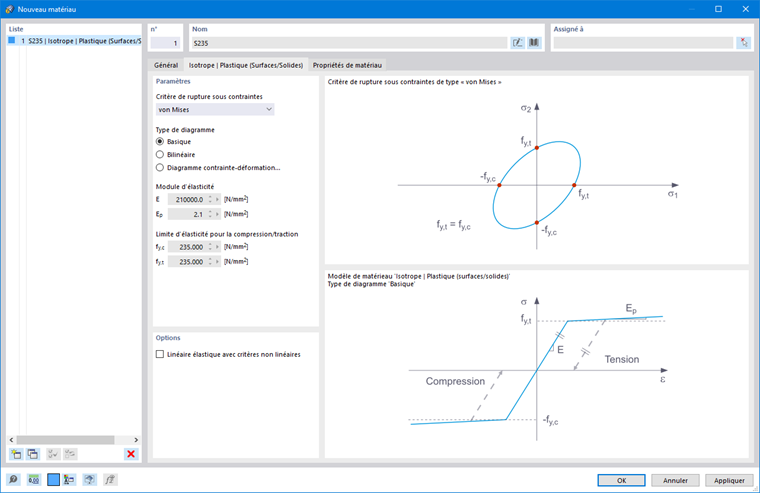
Si Basique est sélectionné, RFEM utilise un modèle de matériau bilinéaire. Les valeurs de la base de données des matériaux sont utilisées pour le module d'élasticité E et la limite d'élasticité f_y. Pour des raisons numériques, la branche du graphe n'est pas exactement horizontale, mais présente une petite pente E_p.

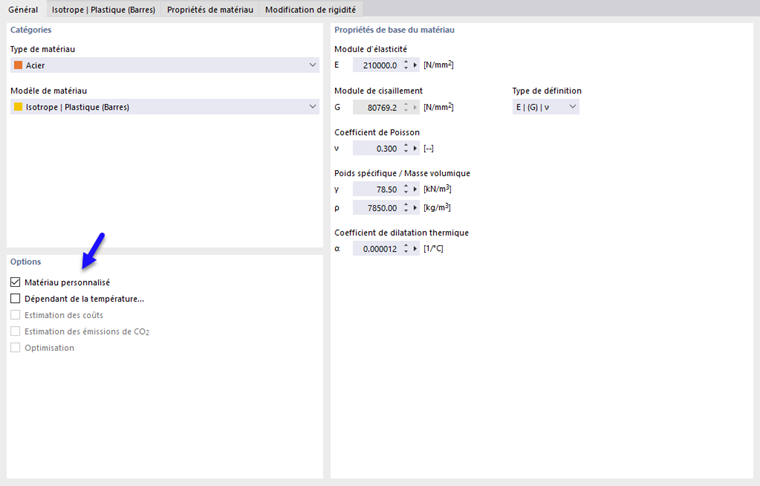
Si vous souhaitez modifier les valeurs de limite d'élasticité et du module d'élasticité, activez la case à cocher "Matériau défini par l'utilisateur" dans l'onglet "Principal".

Activer le matériau défini par l’utilisateur

Pour une définition bilinéaire, vous pouvez également entrer une valeur pour E_p.

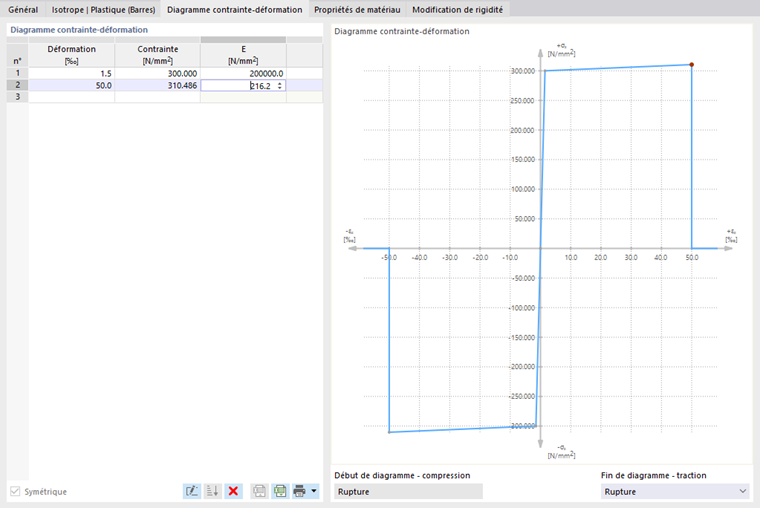
Des relations plus complexes entre contrainte et déformation peuvent être définies au moyen du "Diagramme contrainte-déformation". En sélectionnant cette option, l'onglet "Diagramme Contrainte-Déformation" s'affiche.

Entrer un diagramme contrainte-déformation défini par l’utilisateur

Définissez un point pour la relation contrainte-déformation dans chaque ligne du tableau. Vous pouvez sélectionner comment le diagramme continue après le dernier point de définition dans la liste "Fin du diagramme" sous le diagramme :

Diagramme après le dernier point de définition

Dans le cas de "Déchirement", la contrainte après le dernier point de définition revient à zéro. "Fluage" signifie que la contrainte reste constante lorsque la déformation augmente. "Continu" signifie que le graphe continue avec la pente de la dernière section.

Informations

Dans ce modèle de matériau, le diagramme contrainte-déformation se réfère à la contrainte longitudinale σ_x. Différentes limites d'élasticité pour la traction et la compression ne peuvent pas être considérées par ce modèle de matériau.

Isotrope Plastique | Surfaces/Solides

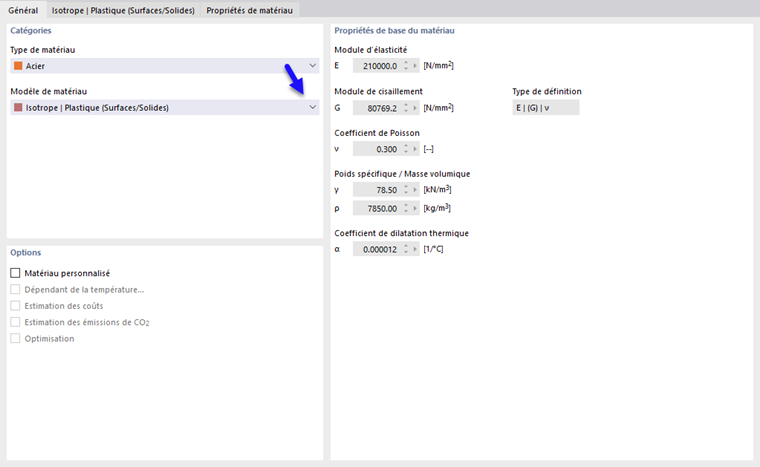
Lors de la sélection de l'entrée "Isotrope | Plastique (Surfaces/Solides)" dans la liste déroulante "Modèle de matériau", l'onglet pour entrer les paramètres de matériau non linéaire est activé.

Sélectionner le modèle de matériau plastique

Tout d'abord, sélectionnez l'"Hypothèse de rupture par contrainte". Les hypothèses suivantes sont disponibles pour la sélection :

von Mises (critère de plastification de von Mises)
Tresca (critère de plastification de Tresca)
Drucker-Prager
Mohr-Coulomb

Définir le critère de rupture sous contrainte

En sélectionnant "von Mises", la contrainte suivante est utilisée dans le diagramme contrainte-déformation :
Surfaces :

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{xy}^{2})}

Contrainte équivalente à partir des contraintes de base selon von Mises

Solides :

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Contrainte équivalente σ_v,Mises à partir des contraintes de base

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Contrainte équivalente σ_{v, Mises} à partir des contraintes principales

Selon l'hypothèse de "Tresca", la contrainte suivante est utilisée :
Surfaces :

σ_{v} = \sqrt{{(σ_{x} - σ_{y})}^{2} + 4 {τ_{xy}}^{2}}

Contraintes équivalentes selon Tresca

Solides :

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Contrainte équivalente σ_v,Tresca

Selon l'hypothèse de "Drucker-Prager", la contrainte suivante est utilisée pour les surfaces et les solides :

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}

m = \frac{σ_{c}}{σ_{t}}

σ_c	Contrainte limite en compression
σ_t	Contrainte limite pour la traction

Critère de rendement selon Drucker-Prager

Selon l'hypothèse de "Mohr-Coulomb", la contrainte suivante est utilisée pour les surfaces et les solides :

σ_{v} = \frac{m + 1}{2} \max \{|σ_{1} - σ_{2}| + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}| + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}| + K (σ_{3} + σ_{1})\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

Mohr-Coulomb

Isotrope Non Linéaire Élastique | Barres

La fonctionnalité correspond largement à celle du modèle de matériau plastique isotrope (barres). La différence réside dans le fait qu'aucune déformation plastique ne reste après le déchargement.

Isotrope Non Linéaire Élastique | Surfaces/Solides

La fonctionnalité correspond largement à celle du modèle de matériau plastique isotrope (surfaces/solides). La différence réside dans le fait qu'aucune déformation plastique ne reste après le déchargement.

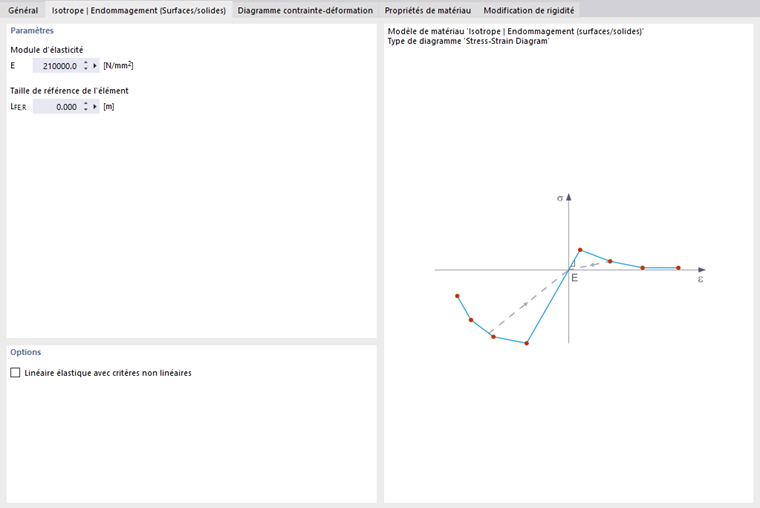
Dommage Isotrope | Surfaces/Solides

Contrairement à d'autres modèles de matériau, le diagramme contrainte-déformation pour ce modèle de matériau n'est pas antimétrique à l'origine. Ainsi, le comportement du béton armé de fibres d'acier peut être affiché avec ce modèle de matériau, par exemple. Trouvez des informations détaillées sur la modélisation du béton armé de fibres d'acier dans l'article technique sur Déterminer les propriétés du matériau des béton armés de fibres d'acier.

Modèle de matériau « Isotrope | Endommagement »

Dans ce modèle de matériau, la raideur isotrope est réduite avec un paramètre de dommage scalaire. Ce paramètre de dommage est déterminé à partir de la courbe de contrainte définie dans le Diagramme. Cela ne prend pas en compte la direction des contraintes principales ; au contraire, le dommage survient dans la direction de la déformation équivalente, qui couvre également la troisième direction perpendiculaire au plan. La zone de tension et de compression du tenseur de contrainte est traitée séparément. Des différents paramètres de dommage s'appliquent dans chaque cas.

La "Taille de l'élément de référence" contrôle comment la déformation dans la zone de fissure est mise à l'échelle en fonction de la longueur de l'élément. Avec la valeur par défaut à zéro, aucune mise à l'échelle n'est effectuée. Ainsi, le comportement du matériau du béton armé de fibres d'acier est modélisé de manière réaliste.

Trouvez plus d'informations sur les fondements théoriques du modèle de matériau "Dommage Isotrope" dans l'article technique décrivant le Modèle de Matériau Non Linéaire Dommage.

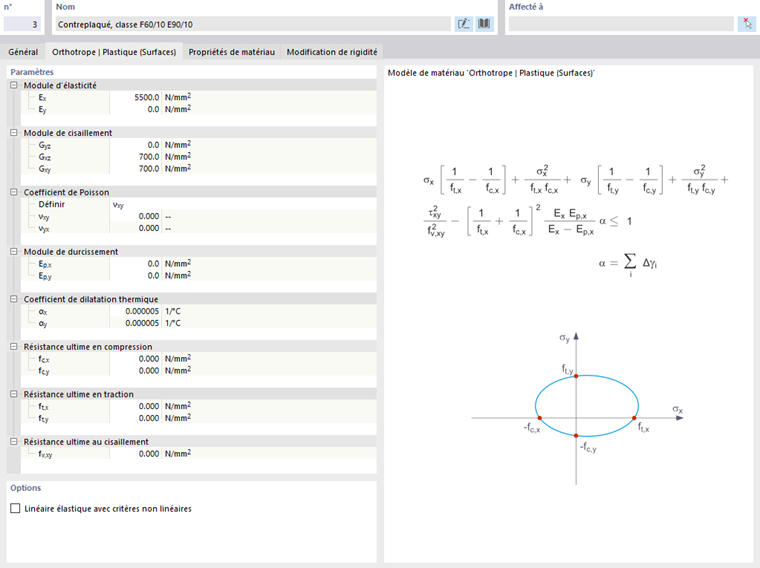
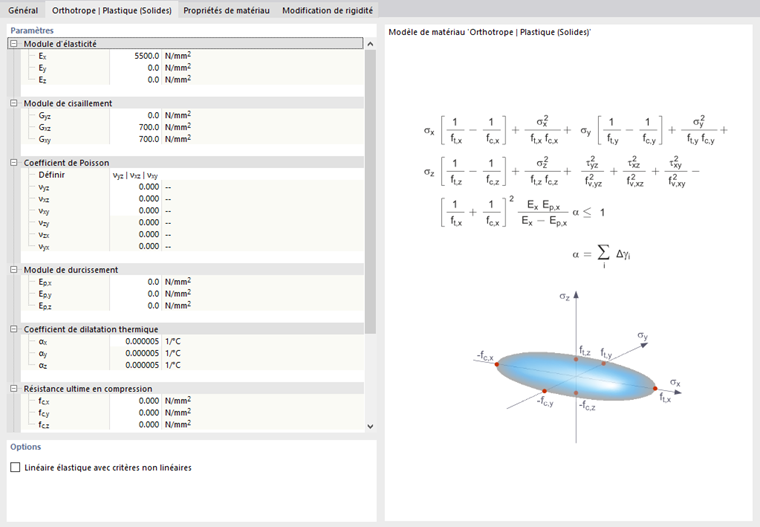
Plastique Orthotrope | Surfaces/Solides

Le modèle de matériau proposé par "Tsai-Wu" unifie les propriétés plastiques avec les propriétés orthotropes. Cela permet une modélisation spéciale des matériaux avec des caractéristiques anisotropes, tels que les plastiques renforcés de fibres ou le bois.

Si le matériau est plastifié, les contraintes restent constantes. La redistribution est effectuée selon les raideurs disponibles dans les différentes directions.

Modèle de matériau « Orthotrope | Plastique (Surfaces) »

Modèle de matériau « Orthotrope | Plastique (Solide) »

La zone élastique correspond au modèle de matériau Orthotrope. La condition de plastification suivante selon Tsai-Wu s'applique à la zone plastique :

Surfaces (2D) :

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

\frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} - {[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu, état de contrainte planaire

Solides (3D) :

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

σ_{z} [\frac{1}{f_{t, z}} - \frac{1}{f_{c, z}}] + \frac{{σ_{z}}^{2}}{f_{t, z} f_{c, z}} +

\frac{{τ_{yz}}^{2}}{{f_{v, yz}}^{2}} + \frac{{τ_{xz}}^{2}}{{f_{v, xz}}^{2}} + \frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} -

{[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu, état de contrainte spatiale

Toutes les résistances doivent être définies positivement.

Vous pouvez concevoir le critère de contrainte comme une surface elliptique dans un espace de contrainte à six dimensions. Si l'une des trois composantes de contrainte est appliquée comme valeur constante, la surface peut être projetée dans un espace de contrainte tridimensionnel.

Si la valeur pour f_y(σ) selon l'équation de Tsai-Wu, condition de contrainte plane, est inférieure à 1, les contraintes sont dans la zone élastique. La zone plastique est atteinte dès que f_y(σ) = 1. Les valeurs supérieures à 1 ne sont pas autorisées. Le comportement du modèle est idéalement plastique, ce qui signifie qu'il n'y a pas de durcissement.

Chapitre parent

Non-linéarité