Pokud je v okně Model – Základní údaje aktivován addon Analýza nelineárního chování materiálu (vyžaduje licenci), jsou v seznamu materiálových modelů k dispozici další možnosti výběru nad rámec materiálových modelů „Izotropní | Lineární elastický“ a „Ortotropní | Lineární elastický“.
Pokud v programu RFEM používáte nelineární materiálové modely, vždy se provádí iterativní výpočet. V závislosti na materiálovém modelu je definován jiný vztah mezi napětími a deformacemi.
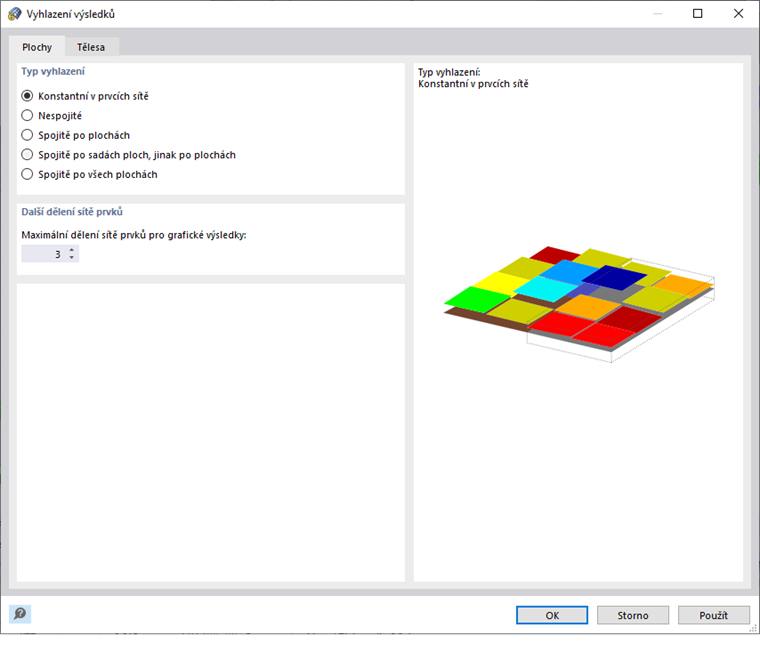
Tuhost konečných prvků se v průběhu iterací opakovaně upravuje, dokud není splněn pracovní diagram. Úprava se vždy provádí pro celý povrchový nebo objemový prvek. Proto doporučujeme při vyhodnocování napětí vždy používat typ vyhlazení prvků Konstantní v prvcích sítě.
Některé materiálové modely v programu RFEM jsou označeny jako „Plastické“, jiné jako „Nelineární elastické“.
Pokud je konstrukční prvek s „nelineárním elastickým“ materiálem znovu uvolněn, přetvoření se vrátí zpět po stejné dráze. Po úplném odlehčení nezůstane žádné přetvoření.
Při odlehčení konstrukčního prvku s plastickým materiálovým modelem zůstává deformace zachována i po úplném odlehčení.
Základní informace o nelineárních materiálových modelech naleznete v technickém článku, který popisuje Podmínky plasticity v izotropním nelineárním elastickém materiálovém modelu.
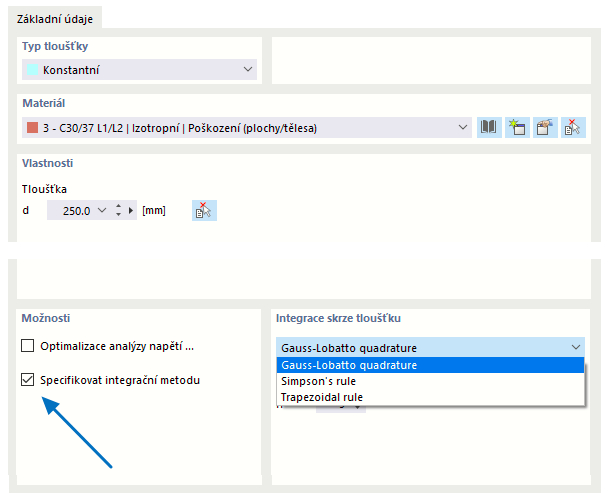
Vnitřní síly a momenty v deskách s nelineárním materiálem jsou výsledkem numerické integrace napětí přes tloušťku d desky. Chcete-li definovat integrační metodu pro tloušťku, vyberte možnost Specifikovat integrační metodu v dialogu „Upravit tloušťku“. K dispozici jsou následující integrační metody:
- Gaussova-Lobattova kvadratura
- Simpsonovo pravidlo
- Lichoběžníkové pravidlo
Dále můžete zadat „Počet integračních bodů“ od 3 do 99 podle tloušťky desky.
Izotropní plastický | Pruty)
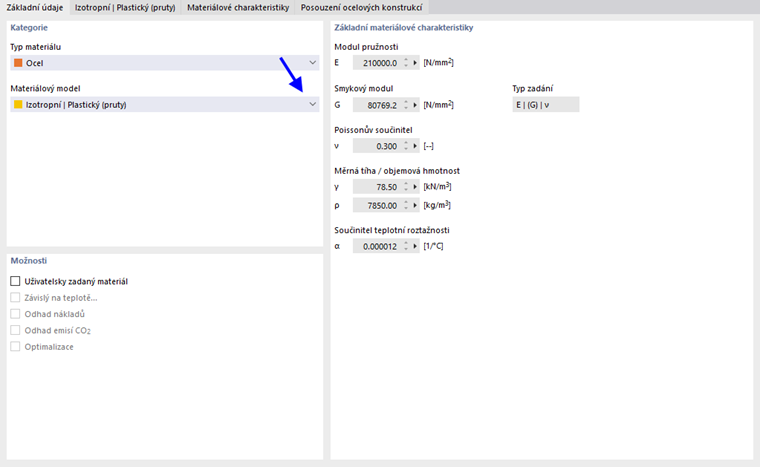
Při výběru položky Materiálový model Izotropní | Plastický (pruty) v rozevíracím seznamu „Materiálový model“ se aktivuje záložka pro zadání nelineárních parametrů materiálu.
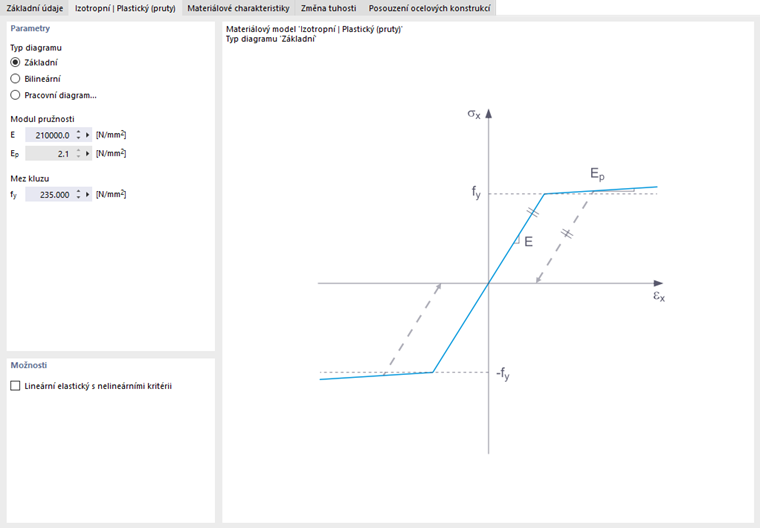
Na této záložce definujete průběh napětí-přetvoření. K dispozici jsou následující možnosti:
- Základní
- Bilineární
- Pracovní diagram
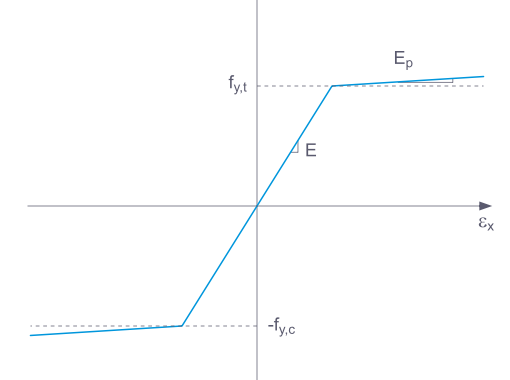
Pokud je vybrána možnost Základní, RFEM použije bilineární materiálový model. Pro modul pružnosti E a mez kluzu fy se použijí hodnoty z materiálové databáze. Z numerických důvodů není větev grafu přesně vodorovná, ale má malý sklon Ep.
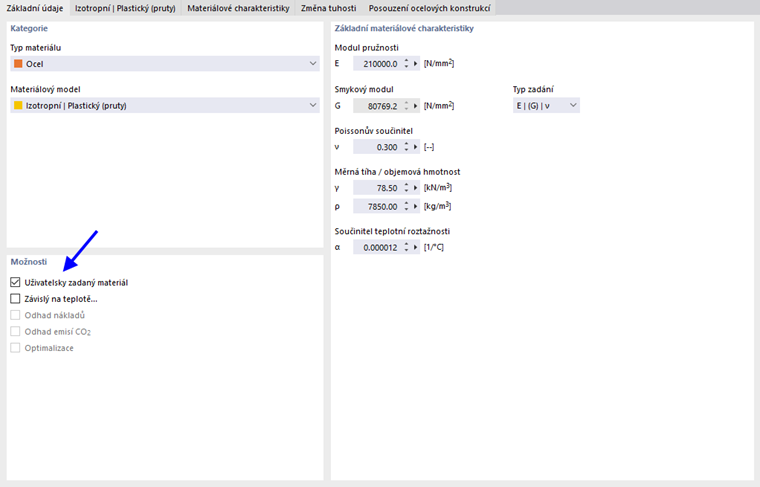
Pokud chcete změnit hodnoty meze kluzu a modulu pružnosti, zaškrtněte políčko „Uživatelsky zadaný materiál“ na záložce Základní údaje.
Pro „bilineární“ definici můžete také zadat hodnotu pro Ep.
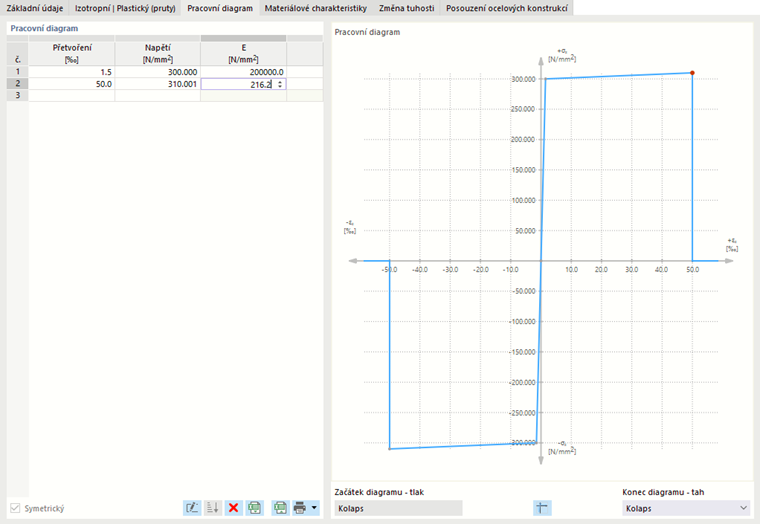
Složitější vztahy mezi napětím a přetvořením lze definovat pomocí „pracovního diagramu“. Při výběru této možnosti se zobrazí záložka „Pracovní diagram“.
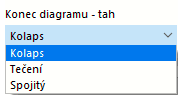
Definujte bod pro pracovní diagram v každém řádku tabulky. V seznamu „Konec diagramu“ pod diagramem můžete vybrat, jak bude diagram pokračovat po posledním definovaném bodě:
V případě „Kolapsu“ se napětí po posledním definovaném bodě vrátí zpět na nulu. „Tečení“ znamená, že napětí zůstává konstantní při zvyšování přetvoření. „Spojitý“ znamená, že graf pokračuje se sklonem poslední části.
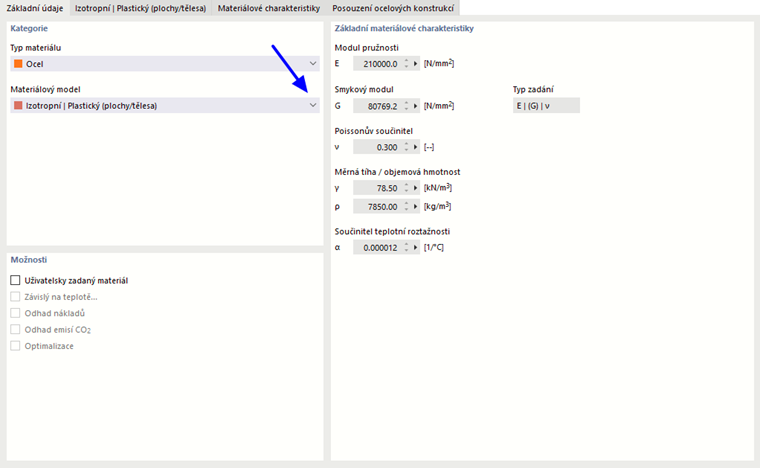
Izotropní | Plastický (plochy/tělesa)
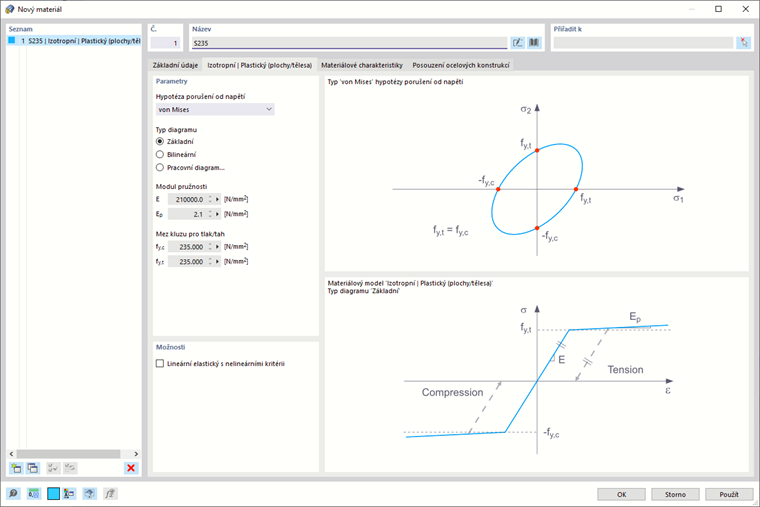
Při výběru položky „Materiálový model Izotropní | Plastický (plochy/tělesa)“ v rozbalovací nabídce „Materiálový model“ se aktivuje záložka pro zadání nelineárních materiálových parametrů.
Nejprve vyberte „Hypotézu porušení od napětí“. K dispozici jsou následující hypotézy:
- von Mises (von Misesovo kritérium meze kluzu)
- Tresca (Trescovo kritérium meze kluzu)
- Drucker-Prager
- Mohr-Coulomb
Při výběru „von Mises“ se v průběhu napětí-přetvoření používá následující napětí:
Plochy:
Tělesa:
Podle „Trescovy“ hypotézy se používá následující napětí:
Plochy:
Tělesa:
Podle hypotézy „Drucker-Prager“ se pro plochy a tělesa používá následující napětí:
Podle hypotézy „Mohr-Coulomb“ se pro plochy a tělesa používá následující napětí:
Izotropní | Nelineárně elastický (pruty)
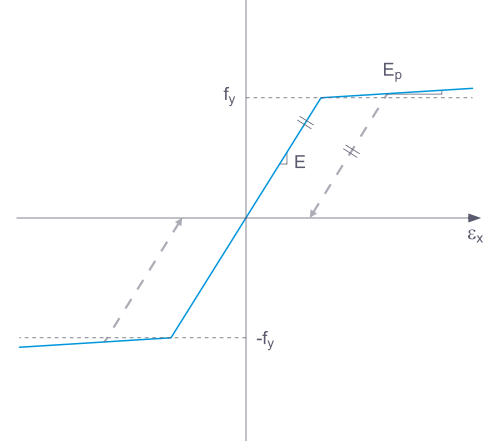
Funkčnost do značné míry odpovídá funkčnosti materiálového modelu Izotropní | Plastický. Rozdíl spočívá v tom, že po odlehčení nezůstává žádné plastické přetvoření.
Izotropní | Nelineárně elastický (plochy/tělesa)
Funkčnost do značné míry odpovídá funkčnosti plastického materiálového modelu (povrchy/tělesa). Rozdíl spočívá v tom, že po uvolnění zatížení nezůstává žádné plastické přetvoření.
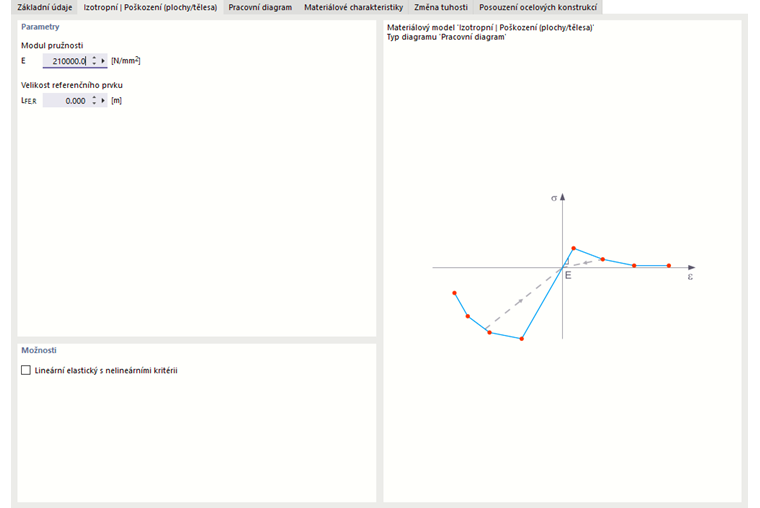
Izotropní | Poškození (plochy/tělesa)
Na rozdíl od jiných materiálových modelů není diagram napětí-přetvoření pro tento materiálový model antimetrický vůči počátku. Pomocí tohoto materiálového modelu lze tedy zobrazit například chování vláknobetonu. Podrobné informace o modelování železobetonu vyztuženého vlákny naleznete v technickém článku o Stanovení materiálových charakteristik železobetonu vyztuženého vlákny.
V tomto materiálovém modelu je izotropní tuhost snížena skalárním parametrem poškození. Tento parametr poškození je určen z křivky napětí definované v diagramu. Nezohledňuje směr hlavních napětí; poškození nastává ve směru ekvivalentního přetvoření, které pokrývá také třetí směr kolmý k rovině. Oblast tahu a tlaku tenzoru napětí je zpracována samostatně. V každém případě platí různé parametry poškození.
„Velikost referenčního prvku“ řídí, jak se přetvoření v oblasti trhliny škálovat na délku prvku. Při výchozí hodnotě nula se žádné škálování neprovádí. Tímto způsobem je chování materiálu vláknobetonu modelováno realisticky.
Více informací o teoretickém pozadí materiálového modelu „Izotropní poškození“ naleznete v technickém článku popisujícím Nelineární materiálový model poškození.
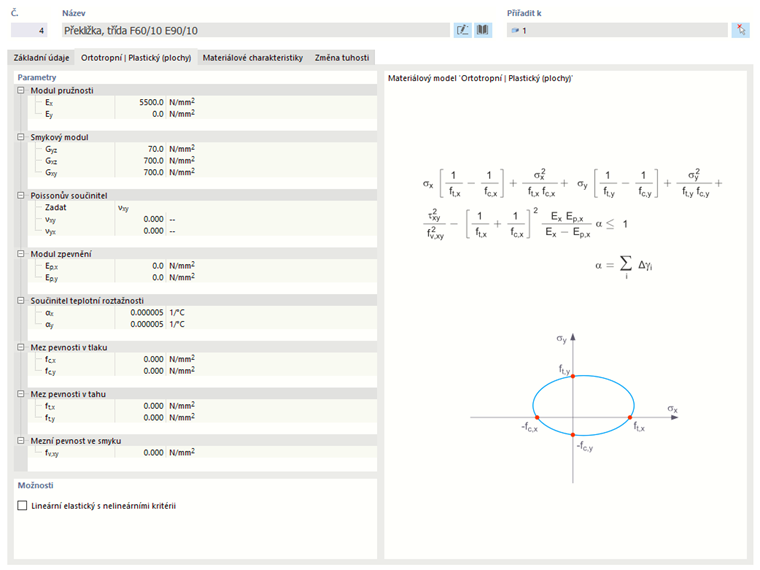
Orthotropní | Plastický (plochy/tělesa)
Materiálový model podle „Tsai-Wu“ sjednocuje plasty s ortotropními vlastnostmi. To umožňuje speciální modelování materiálů s anizotropními vlastnostmi, jako jsou vlákno-plast nebo dřevo.
Pokud je materiál plastifikován, napětí zůstávají konstantní. Redistribuce se provádí podle tuhostí dostupných v jednotlivých směrech.
Elastická oblast odpovídá ortotropnímu materiálovému modelu. Pro plastickou zónu platí následující podmínka tečení podle Tsai-Wu:
Plochy (2D):
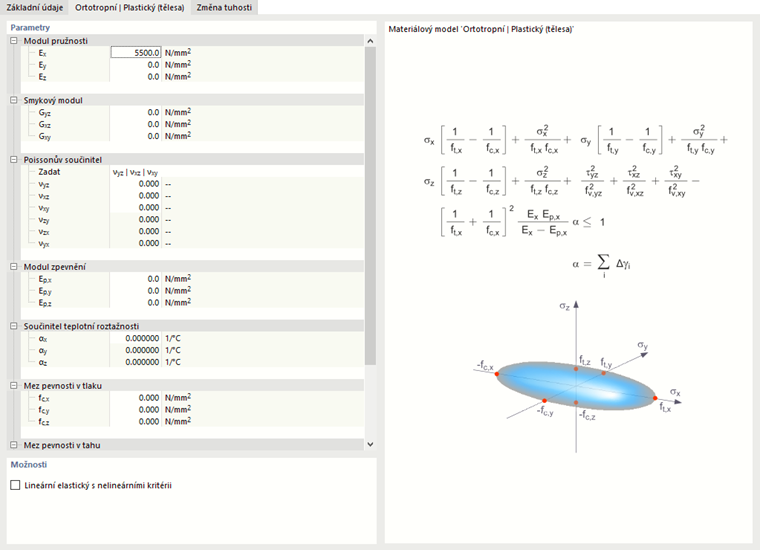
Tělesa (3D):
Všechny pevnosti musí být definovány kladně.
Kritérium napětí si můžete představit jako eliptickou plochu v šestirozměrném prostoru napětí. Pokud je jedna ze tří složek napětí aplikována jako konstantní hodnota, lze plochu promítnout do trojrozměrného prostoru napětí.
Pokud je hodnota fy(σ) podle Tsai-Wuovy rovnice, podmínky rovinného napětí, menší než 1, jsou napětí v elastické zóně. Plastická zóna je dosažena, jakmile fy(σ) = 1. Hodnoty vyšší než 1 nejsou povoleny. Chování modelu je ideálně plastické, což znamená, že nedochází ke ztužení.