4.3 材料

概述

Materialien werden für die Definition von Flächen, Querschnitten und Volumenkörpern benötigt.Die Materialeigenschaften fließen in die Steifigkeiten dieser Objekte ein.

每种材料都分配了一种颜色，用于渲染模型中对象的显示（见 11.1.9 渲染 )RWIND 3。

Bei einem neuen Modell sind die beiden zuletzt benutzten Materialien voreingestellt.

材料描述

Die Bezeichnung für das Material kann beliebig gewählt werden. 如果输入的名称与材料库中包含的材料名称一致，RFEM 会直接导入该材料的属性。

Hinweis
Die Übernahme von Materialien aus der Bibliothek ist im Abschnitt Bibliothek aufrufen beschrieben.

Elastizitätsmodul E

弹性模量 E 是材料正应力与应变的比值。

Über das Menü Bearbeiten → Einheiten und Dezimalstellen oder die zugeordnete Schaltfläche können die Anpassungen für die Materialien vorgenommen werden.

剪切模量 G

剪切模量 G 是描述线性各向同性材料弹性行为的第二个参数，

Hinweis
Der Schubmodul der in der Bibliothek verzeichneten Materialien wird gemäß Gleichung 4.1 aus dem Elastizitätsmodul E und der Querdehnzahl ν berechnet. Damit ist bei isotropen Materialien eine symmetrische Steifigkeitsmatrix gewährleistet.Unter Umständen können die so ermittelten Schubmodul-Werte geringfügig von den Angaben in den Eurocodes abweichen.

Querdehnzahl ν

Zwischen E- und sowie der Querdehnzahl ν (auch Poissonzahl genannt) besteht folgender Zusammenhang:

Hinweis
Werden die Eigenschaften eines isotropen Materials manuell definiert, so ermittelt RFEM automatisch die Querdehnzahl aus den Werten des E- und G-Moduls (bzw. den Schubmodul aus dem E-Modul und der Querdehnzahl).

Bei isotropen Materialien liegt die Querdehnzahl üblicherweise zwischen 0,0 und 0,5.Ab einem Wert von 0,5 (z. B. Gummi) ist daher anzunehmen, dass kein isotropes Material vorliegt. 在计算开始之前会出现是否要使用正交各向异性材料的查询提示。

Spezifisches Gewicht γ

容重 γ 描述了单位体积的材料所承受的重力荷载。

容重对荷载工况‚自重‘尤其重要。 RFEM 通过模型使用的杆件、面和实体的容重和构件体积可以自动计算出模型的自重。

Wärmedehnzahl α

该系数描述了温度变化和长度变化之间的线性关系（热胀冷缩）。

热膨胀系数对荷载类型‚温度变化‘和‚温差‘很重要。

Teilsicherheitsbeiwert γ_M

Dieser Beiwert beschreibt den Sicherheitsfaktor auf der Widerstandsseite für das Material, weshalb der Index M benutzt wird. Mit dem Faktor γ_M kann die Steifigkeit bei der Berechnung abgemindert werden (siehe 7.3.1 荷载工况和组合 )RWIND 3。

Der Beiwert γ_M darf nicht mit den Sicherheitsfaktoren verwechselt werden, die zur Ermittlung der Bemessungsschnittgrößen anzusetzen sind. Die Teilsicherheitsbeiwerte γ auf der Einwirkungsseite fließen bei der Überlagerung der Lastfälle in den Last- und Ergebniskombinationen ein.

材料模型

In der Liste stehen zwölf Materialmodelle zur Auswahl.

使用对话框或表格中的[详细信息]按钮打开相应对话框，在该对话框中可以定义所选材料模型的参数。

Hinweis
Wenn das Zusatzmodul RF-MAT NL nicht lizenziert ist, sind nur die Materialmodelle Isotrop linear elastisch und Orthotrop elastisch 2D/3D nutzbar.

各向同性线弹性

材料为线弹性，且在各个方向上性质相同。 Sie lassen sich gemäß Gleichung 4.1 beschreiben. 适用于以下条件：

• E > 0
• G > 0
• -1 > v ≤ 0,5 (für Flächen und Volumenkörper; für Stäbe nach oben unbegrenzt)

以柔度矩阵形式表达的材料的本构方程如下：

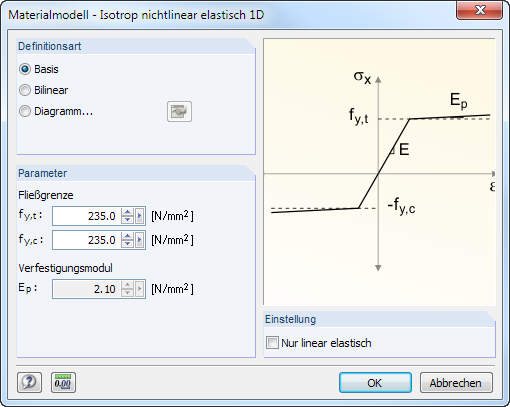
一维各向同性非线性弹性

在对话框中可以定义各向同性材料的非线性弹性的属性。

图片 4.42 材料模型对话框 - 各向同性非线性弹性 1D

Es sind die Fließgrenzen getrennt für Zug (f_y,t) und Druck (f_y,c) des ideal oder bilinear elastischen Materials anzugeben. Zur realitätsgetreuen Abbildung des Materialverhaltens kann auch ein Spannungs-Dehnungs-Diagramm definiert werden (siehe Bild 4.44).

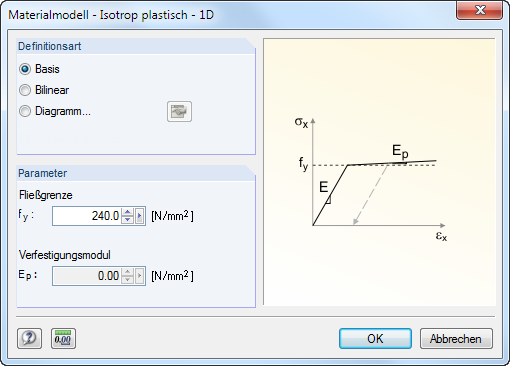
一维各向同性塑性

Liegt der Modelltyp 3D vor (siehe Bild 12.23), können in einem Dialog die plastischen Eigenschaften des isotropen Materials definiert werden. RFEM 会考虑杆件单元的这种材料参数，例如：运动链的塑性计算。

Hinweis
Das nichtlineare Materialverhalten wird in der Berechnung nur dann korrekt erfasst, wenn ausreichend FE-Knoten am Stab erzeugt werden.Hierzu bestehen folgende Möglichkeiten:

• Dialog Stab teilen mittels n Zwischenknoten (siehe Bild 11.91), Teilungsart Nichtteilen der Linie
• Dialog FE-Netz-Einstellungen (siehe Bild 7.10), Option Teilung auch für gerade Stäbe verwenden mit einer Mindestanzahl der Stabteilungen von 10

图 4.43 材料模型对话框 - 各向同性塑性 - 一维

可以输入理想（基本）或双线性塑性材料的参数， Zur realitätsgetreuen Abbildung des Materialverhaltens kann auch ein Spannungs-Dehnungs-Diagramm definiert werden.

图 4.44 对话框 材料模型 - 应力-应变曲线 1D

Die Materialeigenschaften lassen sich getrennt für den positiven und den negativen Bereich definieren. Die Anzahl der Schritte steuert, wie viele Definitionspunkte jeweils vorliegen. In die beiden Listen können dann die Dehnungen ε und die zugehörigen Normalspannungen σ eingetragen werden.

Für den Verlauf nach dem letzten Schritt bestehen mehrere Möglichkeiten: Reißen für den Ausfall des Materials bei Überschreitung, Fließen für die Begrenzung auf die Übertragung einer maximalen Spannung, Fortlaufend wie im letzten Schritt oder Anschlag für die Begrenzung auf eine maximal zulässige Verformung.

也可以从[Excel]表格导入参数。

Die dynamische Grafik im Abschnitt Spannungs-Dehnungs-Diagramm ist hilfreich, um die Materialeigenschaften zu kontrollieren.Im Feld Ei unterhalb der Grafik kann der E-Modul des aktuellen Definitionspunkts abgelesen werden.

在表格中 im Dialog ermöglicht es, das Spannungs-Dehnungs-Diagramm modellübergreifend zu speichern. Mit der Schaltfläche lassen sich benutzerdefinierte Diagramme importieren.

图 4.45 读取对话框数据

Hinweis
Für Stäbe mit isotrop plastischem Materialeigenschaften ist das Kontrollfeld Schubsteifigkeit der Stäbe aktivieren (Querschnittsflächen A_y, A_z) im Berechnungsparameter-Dialog (siehe Bild 7.27) ohne Wirkung. 这种材料模型应用欧拉-伯努利梁理论，不考虑剪切变形。

二维/三维各向同性非线性弹性

Mit diesem Materialmodell können die Eigenschaften nichtlinearer Materialien für Flächen und Volumenkörper abgebildet werden. Es wird keine Energie an das Modell abgegeben (konservative Betrachtung). 因为在加载和卸载时应力-应变图相同，在卸载后没有永久的塑性变形。