Allgemeine Beschreibung
Materialien werden für die Definition von Flächen, Querschnitten und Volumenkörpern benötigt.Die Materialeigenschaften fließen in die Steifigkeiten dieser Objekte ein.
Jedem Material ist eine Farbe zugeordnet, die im gerenderten Modell für die Darstellung der Objekte benutzt wird (siehe 11.1.9 Rendering ).
Bei einem neuen Modell sind die beiden zuletzt benutzten Materialien voreingestellt.
Materialbezeichnung
Die Bezeichnung für das Material kann beliebig gewählt werden. Wenn der eingegebene Name mit einem Eintrag der Bibliothek übereinstimmt, liest RFEM die Materialkennwerte ein.
Hinweis
Die Übernahme von Materialien aus der Bibliothek ist im Abschnitt Bibliothek aufrufen beschrieben.
Elastizitätsmodul E
Der E-Modul beschreibt das Verhältnis zwischen Normalspannung und Dehnung.
Über das Menü Bearbeiten → Einheiten und Dezimalstellen oder die zugeordnete Schaltfläche können die Anpassungen für die Materialien vorgenommen werden.
Schubmodul G
Der Schubmodul G, auch Gleitmodul genannt, ist die zweite Kenngröße zur Beschreibung des elastischen Verhaltens eines linearen, isotropen und homogenen Materials.
Hinweis
Der Schubmodul der in der Bibliothek verzeichneten Materialien wird gemäß Gleichung 4.1 aus dem Elastizitätsmodul E und der Querdehnzahl ν berechnet. Damit ist bei isotropen Materialien eine symmetrische Steifigkeitsmatrix gewährleistet.Unter Umständen können die so ermittelten Schubmodul-Werte geringfügig von den Angaben in den Eurocodes abweichen.
Querdehnzahl ν
Zwischen E- und sowie der Querdehnzahl ν (auch Poissonzahl genannt) besteht folgender Zusammenhang:
Hinweis
Werden die Eigenschaften eines isotropen Materials manuell definiert, so ermittelt RFEM automatisch die Querdehnzahl aus den Werten des E- und G-Moduls (bzw. den Schubmodul aus dem E-Modul und der Querdehnzahl).
Bei isotropen Materialien liegt die Querdehnzahl üblicherweise zwischen 0,0 und 0,5.Ab einem Wert von 0,5 (z. B. Gummi) ist daher anzunehmen, dass kein isotropes Material vorliegt. Vor der Berechnung erscheint die Abfrage, ob ein orthotropes Materialmodell verwendet werden soll.
Spezifisches Gewicht γ
Das spezifische Gewicht γ beschreibt das Gewicht des Materials je Volumeneinheit.
Die Angabe ist insbesondere für den Lastfall ‚Eigengewicht‘ bedeutsam. Die automatische Eigenlast des Modells wird aus dem spezifischen Gewicht und den Querschnittsflächen der verwendeten Stäbe bzw. den Flächen und Volumenkörpern ermittelt.
Wärmedehnzahl α
Dieser Koeffizient der Materialeigenschaft beschreibt den linearen Zusammenhang zwischen Temperatur- und Längenänderungen (Dehnung bei Erwärmung, Stauchung bei Abkühlung).
Die Wärmedehnzahl ist für die Lastarten ‚Temperaturänderung‘ und ‚Temperaturdifferenz‘ relevant.
Teilsicherheitsbeiwert γM
Dieser Beiwert beschreibt den Sicherheitsfaktor auf der Widerstandsseite für das Material, weshalb der Index M benutzt wird. Mit dem Faktor γM kann die Steifigkeit bei der Berechnung abgemindert werden (siehe 7.3.1 Lastfälle und Lastkombinationen ).
Der Beiwert γM darf nicht mit den Sicherheitsfaktoren verwechselt werden, die zur Ermittlung der Bemessungsschnittgrößen anzusetzen sind. Die Teilsicherheitsbeiwerte γ auf der Einwirkungsseite fließen bei der Überlagerung der Lastfälle in den Last- und Ergebniskombinationen ein.
Materialmodell
In der Liste stehen zwölf Materialmodelle zur Auswahl.
Die [Details]-Schaltfläche im Dialog bzw. in der Tabelle ermöglicht den Zugang zu Dialogen, in denen die Parameter des gewählten Modells definiert werden können.
Hinweis
Wenn das Zusatzmodul
RF-MAT NL
nicht lizenziert ist, sind nur die Materialmodelle Isotrop linear elastisch und Orthotrop elastisch 2D/3D nutzbar.
Isotrop linear elastisch
Die linear-elastischen Steifigkeitseigenschaften des Materials sind unabhängig von der Richtung. Sie lassen sich gemäß Gleichung 4.1 beschreiben. Es gelten folgende Bedingungen:
- E > 0
- G > 0
- -1 > v ≤ 0,5 (für Flächen und Volumenkörper; für Stäbe nach oben unbegrenzt)
Die Nachgiebigkeitsmatrix (Umkehrung der Steifigkeitsmatrix) lautet für Flächen:
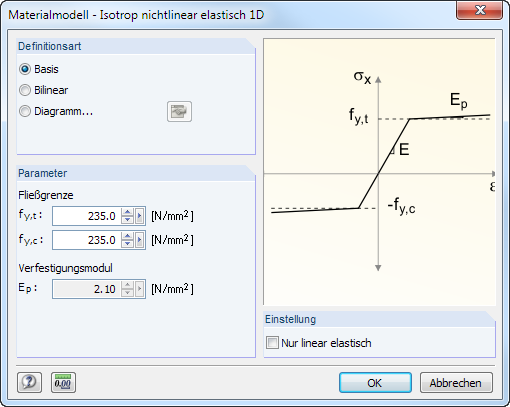
Isotrop nichtlinear elastisch 1D
In einem Dialog können die nichtlinearen Eigenschaften eines isotropen Materials festgelegt werden.
Es sind die Fließgrenzen getrennt für Zug (fy,t) und Druck (fy,c) des ideal oder bilinear elastischen Materials anzugeben. Zur realitätsgetreuen Abbildung des Materialverhaltens kann auch ein Spannungs-Dehnungs-Diagramm definiert werden (siehe Bild 4.44).
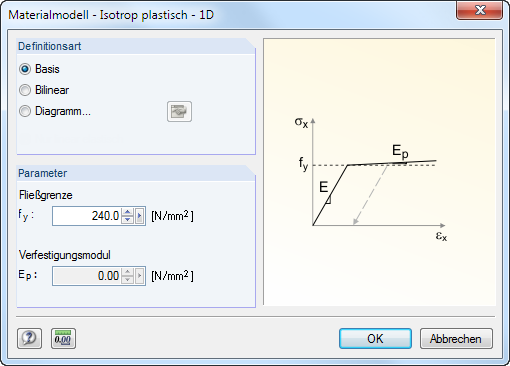
Isotrop plastisch 1D
Liegt der Modelltyp 3D vor (siehe Bild 12.23), können in einem Dialog die plastischen Eigenschaften des isotropen Materials definiert werden. RFEM berücksichtigt diese Materialparameter für Stabelemente z. B. zur plastischen Berechnung einer kinematischen Kette.
Hinweis
Das nichtlineare Materialverhalten wird in der Berechnung nur dann korrekt erfasst, wenn ausreichend FE-Knoten am Stab erzeugt werden.Hierzu bestehen folgende Möglichkeiten:
- Dialog Stab teilen mittels n Zwischenknoten (siehe Bild 11.91), Teilungsart Nichtteilen der Linie
- Dialog FE-Netz-Einstellungen (siehe Bild 7.10), Option Teilung auch für gerade Stäbe verwenden mit einer Mindestanzahl der Stabteilungen von 10
Es sind die Parameter des ideal oder bilinear plastischen Materials anzugeben. Zur realitätsgetreuen Abbildung des Materialverhaltens kann auch ein Spannungs-Dehnungs-Diagramm definiert werden.
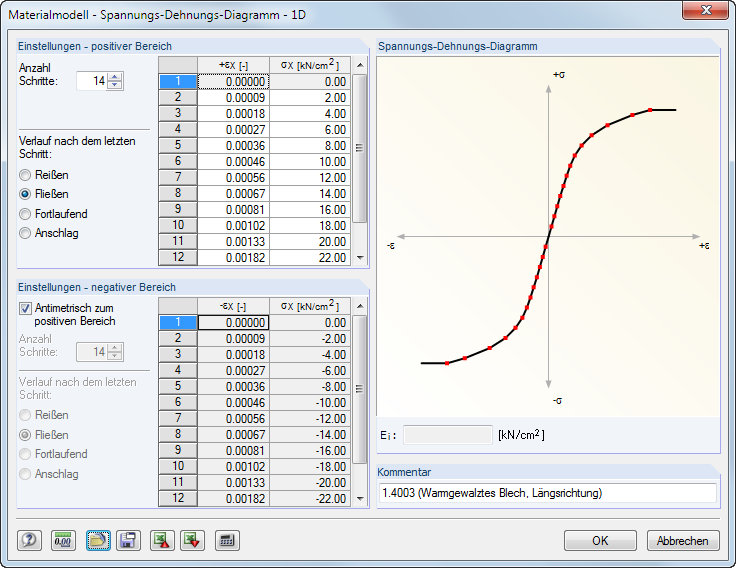
Die Materialeigenschaften lassen sich getrennt für den positiven und den negativen Bereich definieren. Die Anzahl der Schritte steuert, wie viele Definitionspunkte jeweils vorliegen. In die beiden Listen können dann die Dehnungen ε und die zugehörigen Normalspannungen σ eingetragen werden.
Für den Verlauf nach dem letzten Schritt bestehen mehrere Möglichkeiten: Reißen für den Ausfall des Materials bei Überschreitung, Fließen für die Begrenzung auf die Übertragung einer maximalen Spannung, Fortlaufend wie im letzten Schritt oder Anschlag für die Begrenzung auf eine maximal zulässige Verformung.
Die Kennwerte können auch aus einer [Excel]-Tabelle eingelesen werden.
Die dynamische Grafik im Abschnitt Spannungs-Dehnungs-Diagramm ist hilfreich, um die Materialeigenschaften zu kontrollieren.Im Feld Ei unterhalb der Grafik kann der E-Modul des aktuellen Definitionspunkts abgelesen werden.
Die Schaltfläche
im Dialog ermöglicht es, das Spannungs-Dehnungs-Diagramm modellübergreifend zu speichern. Mit der Schaltfläche
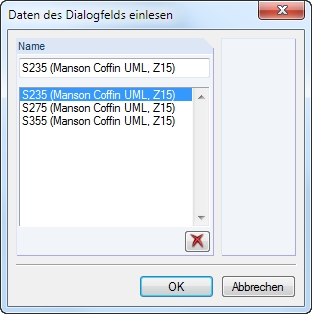
lassen sich benutzerdefinierte Diagramme importieren.
Hinweis
Für Stäbe mit isotrop plastischem Materialeigenschaften ist das Kontrollfeld Schubsteifigkeit der Stäbe aktivieren (Querschnittsflächen Ay, Az) im Berechnungsparameter-Dialog (siehe Bild 7.27) ohne Wirkung. Dieses Materialmodell verwendet die Balkentheorie nach Euler-Bernoulli, bei der Schubverzerrungen vernachlässigt werden.
Isotrop nichtlinear elastisch 2D/3D
Mit diesem Materialmodell können die Eigenschaften nichtlinearer Materialien für Flächen und Volumenkörper abgebildet werden. Es wird keine Energie an das Modell abgegeben (konservative Betrachtung). Da die gleichen Spannungs-Dehnungs-Beziehungen für Belastung und Entlastung gelten, liegen nach einer Entlastung keine dauerhaften plastischen Verzerrungen vor.