4.3 Matériaux

Description générale

Materialien werden für die Definition von Flächen, Querschnitten und Volumenkörpern benötigt.Die Materialeigenschaften fließen in die Steifigkeiten dieser Objekte ein.

Chaque matériau est représenté par une Couleur qui est utilisée pour l'affichage des objets dans le modèle rendu (voir 11.1.9 Rendu ).

Pour de nouveaux modèles, RFEM prédéfinit les deux matériaux utilisés en dernier.

Description du matériau

Vous pouvez choisir un nom pour la Description du matériau. Si le nom inséré correspond à une entrée de la bibliothèque, RFEM importe les propriétés de matériau.

Remarque
L'importation des matériaux de la bibliothèque est décrit dans le Chapitre Ouverture de la bibliothèque.

Module d’élasticité E

Le module d'élasticité E décrit le rapport entre la contrainte normale et la déformation axiale.

Über das Menü Bearbeiten → Einheiten und Dezimalstellen oder die zugeordnete Schaltfläche können die Anpassungen für die Materialien vorgenommen werden.

Module de cisaillement G

Le module de cisaillement G est le deuxième paramètre utilisé pour décrire le comportement élastique d’un matériau homogène, isotrope et linéaire.

Remarque
Der Schubmodul der in der Bibliothek verzeichneten Materialien wird gemäß Gleichung 4.1 aus dem Elastizitätsmodul E und der Querdehnzahl ν berechnet. Damit ist bei isotropen Materialien eine symmetrische Steifigkeitsmatrix gewährleistet.Unter Umständen können die so ermittelten Schubmodul-Werte geringfügig von den Angaben in den Eurocodes abweichen.

Querdehnzahl ν

Zwischen E- und sowie der Querdehnzahl ν (auch Poissonzahl genannt) besteht folgender Zusammenhang:

Remarque
Werden die Eigenschaften eines isotropen Materials manuell definiert, so ermittelt RFEM automatisch die Querdehnzahl aus den Werten des E- und G-Moduls (bzw. den Schubmodul aus dem E-Modul und der Querdehnzahl).

Bei isotropen Materialien liegt die Querdehnzahl üblicherweise zwischen 0,0 und 0,5.Ab einem Wert von 0,5 (z. B. Gummi) ist daher anzunehmen, dass kein isotropes Material vorliegt. Avant le démarrage du calcul, il vous est demandé si vous voulez utiliser un matériau de type orthotrope.

Spezifisches Gewicht γ

Le poids spécifique γ décrit le poids du matériau par unité de volume.

Cette spécification est importante surtout pour le type de charge « poids propre ». le poids propre automatique du modèle est déterminé par le poids spécifique et les aires de section des barres, surfaces ou solides utilisés.

Wärmedehnzahl α

Le coefficient décrit une corrélation linéaire entre les changements de température et les déformations axiales (allongement dû à la chaleur, rétrécissement dû au froid).

La valeur est importante pour les types de charge « variations de température » et « température différentielle ».

Facteur partiel de sécurité du matériau γ_M

La valeur décrit le facteur de sécurité pour la résistance de matériau. Ainsi, l'indice M est utilisé. Mit dem Faktor γ_M kann die Steifigkeit bei der Berechnung abgemindert werden (siehe 7.3.1 Cas de charge et combinaisons ).

Der Beiwert γ_M darf nicht mit den Sicherheitsfaktoren verwechselt werden, die zur Ermittlung der Bemessungsschnittgrößen anzusetzen sind. Die Teilsicherheitsbeiwerte γ auf der Einwirkungsseite fließen bei der Überlagerung der Lastfälle in den Last- und Ergebniskombinationen ein.

Modèle de matériau

Douze modèles de matériau peuvent être sélectionnés dans la liste.

À l'aide du bouton [Détails] de la boîte de dialogue, ou du tableau, vous pouvez accéder aux boîtes de dialogue permettant la définition des paramètres du modèle sélectionné.

Remarque
Wenn das Zusatzmodul RF-MAT NL nicht lizenziert ist, sind nur die Materialmodelle Isotrop linear elastisch und Orthotrop elastisch 2D/3D nutzbar.

Isotrope linéaire élastique

Les propriétés de rigidité élastique linéaires du matériau ne dépendent pas des directions. Sie lassen sich gemäß Gleichung 4.1 beschreiben. Les conditions suivantes sont appliquées :

• E > 0
• G > 0
• -1 > v ≤ 0,5 (für Flächen und Volumenkörper; für Stäbe nach oben unbegrenzt)

La matrice d'élasticité (inverse de la matrice de rigidité) pour les surfaces est la suivante :

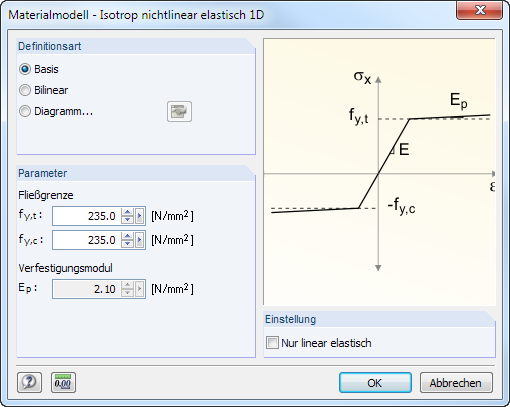
Isotrope élastique non-linéaire 1D

Vous pouvez définir les propriétés élastiques non-linéaires du matériau isotrope dans la boîte de dialogue.

Image 4.42 Boîte de dialogue Modèle de matériau - Isotrope non linéaire élastique 1D

Es sind die Fließgrenzen getrennt für Zug (f_y,t) und Druck (f_y,c) des ideal oder bilinear elastischen Materials anzugeben. Zur realitätsgetreuen Abbildung des Materialverhaltens kann auch ein Spannungs-Dehnungs-Diagramm definiert werden (siehe Bild 4.44).

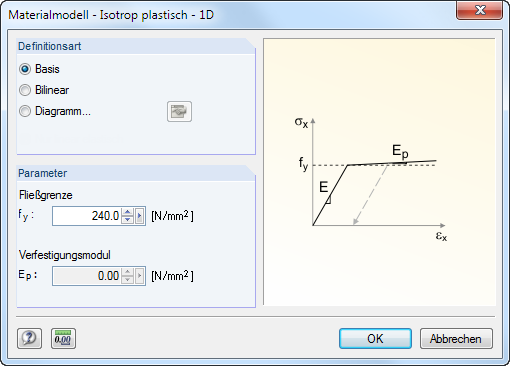
Isotrope plastique 1D

Liegt der Modelltyp 3D vor (siehe Bild 12.23), können in einem Dialog die plastischen Eigenschaften des isotropen Materials definiert werden. RFEM va prendre en compte ces propriétés pour les éléments de barre, par exemple pour les calculs plastiques d'une chaîne cinématique.

Remarque
Das nichtlineare Materialverhalten wird in der Berechnung nur dann korrekt erfasst, wenn ausreichend FE-Knoten am Stab erzeugt werden.Hierzu bestehen folgende Möglichkeiten:

• Dialog Stab teilen mittels n Zwischenknoten (siehe Bild 11.91), Teilungsart Nichtteilen der Linie
• Dialog FE-Netz-Einstellungen (siehe Bild 7.10), Option Teilung auch für gerade Stäbe verwenden mit einer Mindestanzahl der Stabteilungen von 10

Image 4.43 Boîte de dialogue du modèle de matériau - Isotrope plastique - 1D

Définissez les paramètres du matériau plastique idéal ou bilinéaire. Zur realitätsgetreuen Abbildung des Materialverhaltens kann auch ein Spannungs-Dehnungs-Diagramm definiert werden.

Image 4.44 Boîte de dialogue Modèle de matériau - Diagramme contrainte-déformation 1D

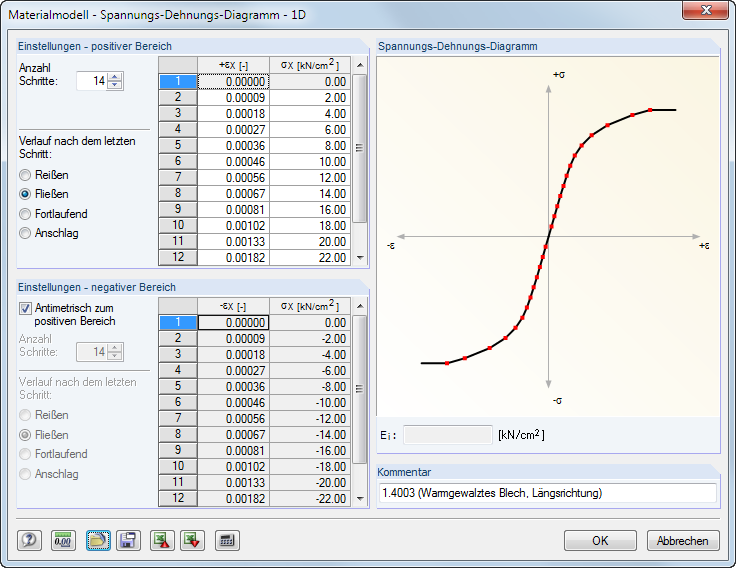
Die Materialeigenschaften lassen sich getrennt für den positiven und den negativen Bereich definieren. Die Anzahl der Schritte steuert, wie viele Definitionspunkte jeweils vorliegen. In die beiden Listen können dann die Dehnungen ε und die zugehörigen Normalspannungen σ eingetragen werden.

Für den Verlauf nach dem letzten Schritt bestehen mehrere Möglichkeiten: Reißen für den Ausfall des Materials bei Überschreitung, Fließen für die Begrenzung auf die Übertragung einer maximalen Spannung, Fortlaufend wie im letzten Schritt oder Anschlag für die Begrenzung auf eine maximal zulässige Verformung.

L'import des paramètres depuis une feuille [Excel] est également possible.

Die dynamische Grafik im Abschnitt Spannungs-Dehnungs-Diagramm ist hilfreich, um die Materialeigenschaften zu kontrollieren.Im Feld Ei unterhalb der Grafik kann der E-Modul des aktuellen Definitionspunkts abgelesen werden.

Le tableau im Dialog ermöglicht es, das Spannungs-Dehnungs-Diagramm modellübergreifend zu speichern. Les boutons lassen sich benutzerdefinierte Diagramme importieren.

Image 4.45 Lire les données de la boîte de dialogue

Remarque
Für Stäbe mit isotrop plastischem Materialeigenschaften ist das Kontrollfeld Schubsteifigkeit der Stäbe aktivieren (Querschnittsflächen A_y, A_z) im Berechnungsparameter-Dialog (siehe Bild 7.27) ohne Wirkung. Ce modèle de matériau utilise la théorie des poutres selon Euler-Bernoulli, dans laquelle les distorsions de cisaillement sont négligées.

Isotrope élastique non-linéaire 2D/3D

Avec ce modèle de matériau vous pouvez afficher les propriétés des matériaux non-linéaires pour les surfaces et les solides. Aucune énergie n'est livrée dans le modèle (analyse conservatrice). Les mêmes relations contrainte-déformation étant appliquées pour le chargement et le déchargement, il n'y a aucune déformation permanente après un déchargement.