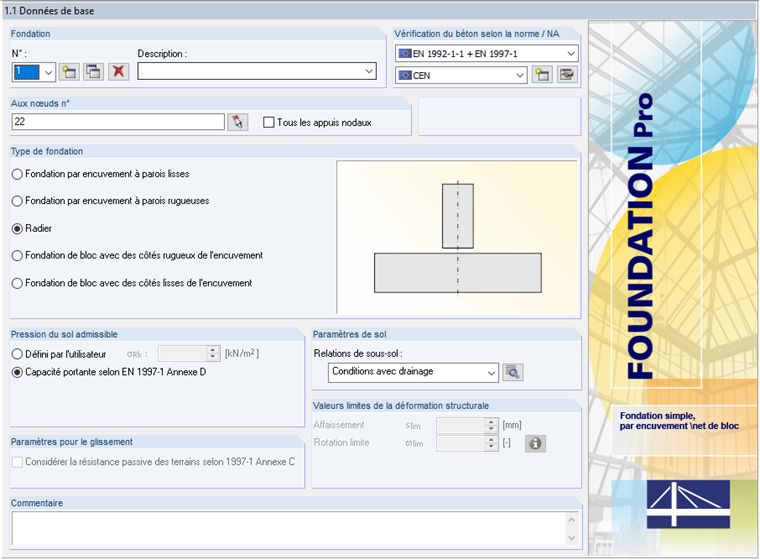
L’exemple suivant vous montre cette détermination. Demnach ist in Maske 1.1 Basisangaben die Auswahl "Grundbruchwiderstand nach EN 1997-1 Anhang D" vorzunehmen. Im hier beschriebenen Nachweisverfahren wird das "Verfahren 2" beschrieben, welches bei der Bemessung mit der NA-Auswahl "CEN" voreingestellt ist.
Bodenschichten und Bodenkennwerte
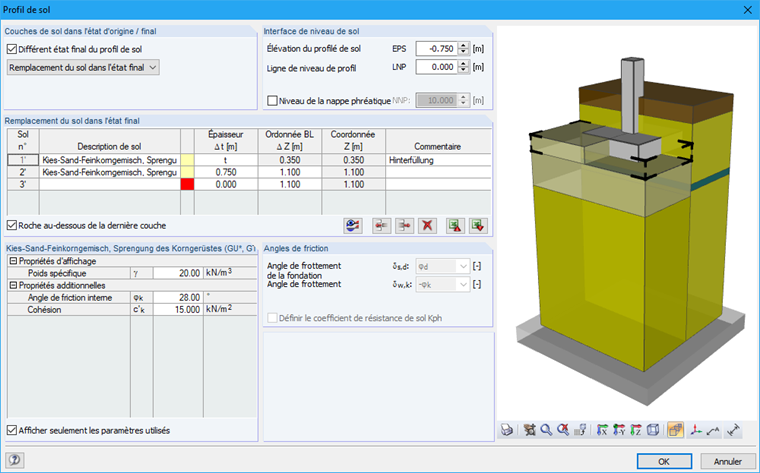
Für die Ermittlung des Grundbruchwiderstandes ist zunächst ein Bodenprofil anzugeben, welches für den Nachweis berücksichtigt werden soll. Nachfolgend wird hierzu das Bodenprofil im Endzustand betrachtet, da dieses für die analytische Ermittlung des Grundbruchwiderstandes zu Grunde gelegt wird.
Die Bodenschichten neben dem Fundament (Schicht 1') und bis zu 0,75 m unter der Fundamentsohle (Schicht 2') weisen hierbei folgende Bodenkennwerte auf:
Poids spécifique : γ = 20,00 kN/m³
Winkel der inneren Reibung: φk = 28,0°
Kohäsion: c'k = 15,00 kN/m²
Die Bodenschicht unterhalb des Bodenaustausches (Schicht 3, aus ursprünglichem Bodenprofil) weist folgende Bodenparameter auf:
Poids spécifique : γ = 20,00 kN/m³
Winkel der inneren Reibung: φk = 32,0°
keine Kohäsion: c'k = 0,00 kN/m²
Dimensions des radiers
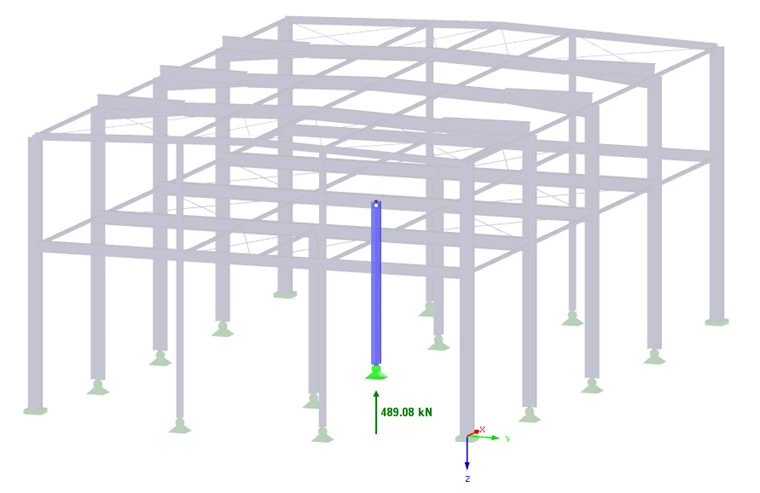
Die Berechnung der zulässigen Sohldruckspannung soll in diesem Beispiel für eine rechteckige Fundamentplatte mit den Abmessungen 1,50 m · 1,50 m · 0,35 m durchgeführt werden. In dem vorliegenden Modell soll der Grundbruchnachweis für eine Fundamentplatte einer Stahlhalle geführt werden. Mittig auf der Fundamentplatte wird eine Pendelstütze der Stahlhalle angeordnet, wodurch die Fundamentplatte mit einer Vertikallast von Vd = 489,08 kN belastet wird. Die nachfolgende Grafik zeigt die Stütze in der Stahlhalle mit der maßgeblichen Lagerreaktion P-Z.
Bestimmung des Grundbruchwiderstandes
Der charakteristische Wert des Grundbruchwiderstandes lässt sich nach [1] Anhang D, Gleichung (D.2) für konsolidierte Verhältnisse bestimmen zu:
In einem ersten Schritt werden zunächst die wirksamen Bodenkennwerte bestimmt, da unterhalb der Fundamentsohle zwei verschiedene Böden mit unterschiedlichen Bodenkennwerten anliegen. Die ermittelte Tiefe des Grundbruchkegels ergibt sich in diesem Beispiel zu zs = 2,443 m. Demnach wird die Schicht 3 unter der Fundamentsohle mit einer Tiefe von 2,443 m - 0,75 m = 1,693 m angeschnitten.
Wirksame Bodenkennwerte:
γ' = 20 kN/m³
Wirksame Auflast auf Sohlniveau:
q' = 0,35 m · 20 kN/m³ = 7,0 kN/m²
Im nächsten Schritt werden die dimensionslosen Faktoren für die Tragfähigkeit, Sohlflächenneigung, die Grundrissform des Fundaments und der Lastneigung infolge einer Horizontalkraft ermittelt.
Dimensionslose Faktoren für die Tragfähigkeit:
Nq = eπ · tanφ' · tan² (45 + φ' / 2) = 20,096
Nc = (Nq - 1) · cos φ' = 32,069
Nγ = 2 · (Nq - 1) · tan φ' = 22,741
In diesem Beispiel wird eine Fundamentplatte mit einer quadratischen Grundrissform untersucht. Demnach ergeben sich folgende dimensionslose Faktoren für die Grundrissform zu:
sq = 1 + sin φ' = 1,512
sγ = 0,70
sc = (sq · Nq - 1) / (Nq - 1) = 1,538
In diesem Zusammenhang sei darauf hingewiesen, dass für die Fundamentabmessungen die rechnerische Sohlflächenlänge L' und Sohlflächenbreite B' einzusetzen sind. Da in diesem Fall lediglich eine Vertikallast untersucht wird und die Lastexzentrizität gleich Null ist, ergibt sich L' = B' = 1,50 m und hieraus die Einordung als "quadratisches Fundament". Würde an dem Fundament eine Horizontallast angreifen, ergäbe sich aus den unterschiedlichen rechnerischen Sohlflächenlängen L' und -breiten B' entsprechend ein rechteckiger rechnerischer Fundamentgrundriss.
Die dimensionslosen Faktoren für die Sohlflächenneigung bc, bq und bγ ergeben sich zu 1,00, da der Grundbruchnachweis in RF-/FUND Pro grundsätzlich für horizontale Fundamentplatten (α = 0°) geführt wird. Die dimensionslosen Faktoren für die Lastneigung infolge einer Horizontallast H ergeben sich in diesem Beispiel ebenfalls zu 1,00, da keine Horizontallasten angreifen.
Mit den nun vorliegenden Eingangsparametern kann der charakteristische Wert des Grundbruchwiderstands nach (D.2) ermittelt werden:
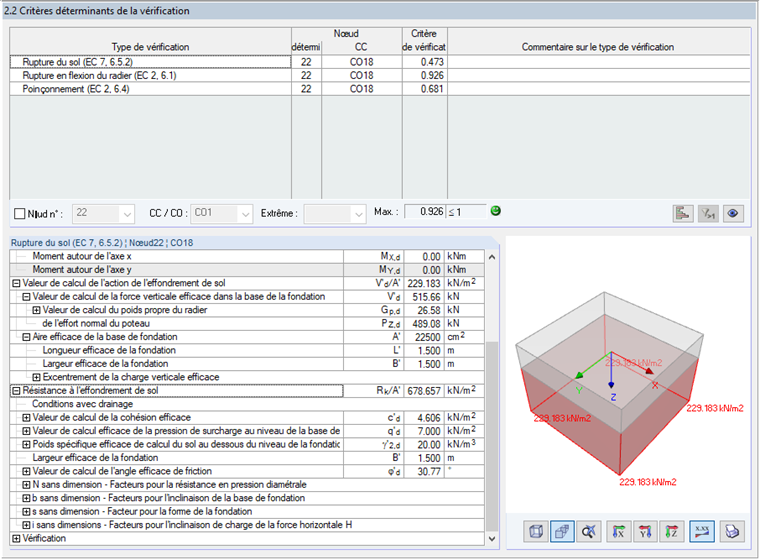
Nachweiskriterium für den Grundbruchnachweis
Wie eingangs erwähnt, wird in diesem Beispiel die Berechnung nach CEN mit dem Verfahren 2 angesprochen. Aus den Parametern des Nationalen Anhang ist in diesem Fall (gemäß [1] Tabelle A.5) ein Teilsicherheitsbeiwert für den Grundbruch von γR,v = 1,4 vorzusehen.
Demnach ergibt sich der Bemessungswert des Grundbruchwiderstandes zu:
Die vorhandene Sohlspannung V'd / A' ergibt sich aus der Summe der Spannungen aus der Normalkraft in der Stütze und dem Fundamentplatteneigengewicht:
Nachweiskriterium:
Weitere Hinweise zum Grundbruchnachweis in RF-/FUND Pro finden sich auch im zugehörigen Handbuch. Im Abschnitt 8.4 des Handbuchs wird ebenfalls auf die Ermittlung des Grundbruchwiderstandes eingegangen. Des Weiteren werden hier auch die Unterschiede zwischen dem Nachweisverfahren 2 und 2* angesprochen.