8360x

001442

Dipl.-Ing. (FH) Paul Kieloch

2017-05-23

Determining Bearing Resistance According to EN 1997-1

In addition to the reinforced concrete design according to EN 1992‑1‑1, RF-/FOUNDATION Pro allows you to perform geotechnical designs according to EN 1997‑1. In RF-/FOUNDATION Pro, the design of the allowable soil pressure is performed as a ground failure resistance design. If you select CEN as National Annex, you have two options for defining the ground failure resistance. First, you can directly specify the allowable characteristic value of the soil pressure σ_Rk. Second, there is also the option to analytically determine the bearing capacity according to [1], Annex D.

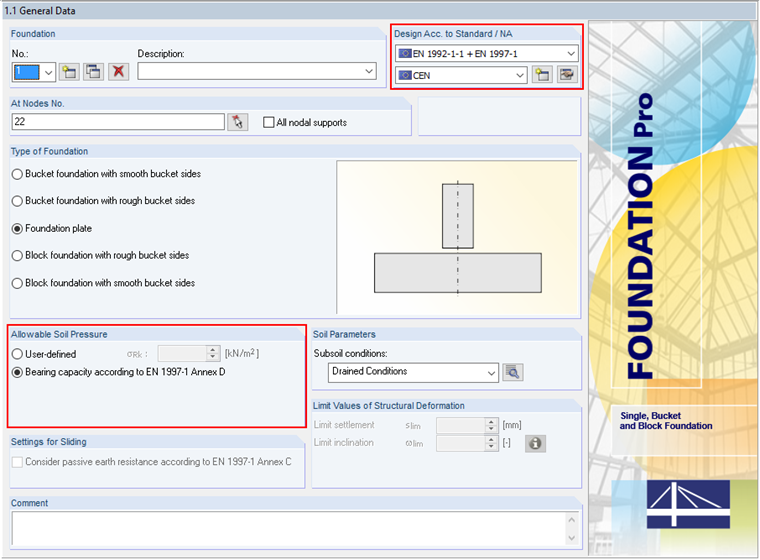
Specifications for Determining Allowable Soil Pressure

The following example shows this determination. In Window 1.1 General Data, we select the "Bearing capacity according to EN 1997‑1 Annex D" option. The analytical method described herein includes "Method 2", which is preset by default when selecting "CEN" as the NA of the design standard.

Soil Layers and Soil Properties

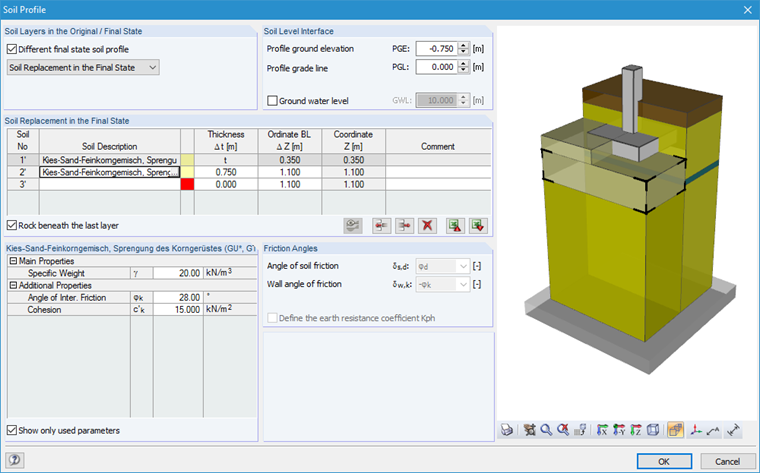
When determining the bearing resistance, it is necessary to specify a soil profile first, which is to be taken into account for the design. Then, the soil profile in the final state is considered as the analytical determination of the bea resistance is based on this.

In our example, the soil layers adjacent to the foundation (Soil 1') and up to 0.75 m below the foundation base (Soil 2') have the following soil properties:
Specific Weight: γ = 20.00 kN/m³
Angle of internal friction: φ_k = 28.0°
Cohesion: c'_k = 15.00 kN/m²

Soil Profile in Final State

The soil layer below the soil replacement (Soil 3, from the original soil profile) has the following soil parameters:
Specific Weight: γ = 20.00 kN/m³
Angle of internal friction: φ_k = 32.0°
No cohesion: c'_k = 0.00 kN/m²

Foundation Plate Dimensions

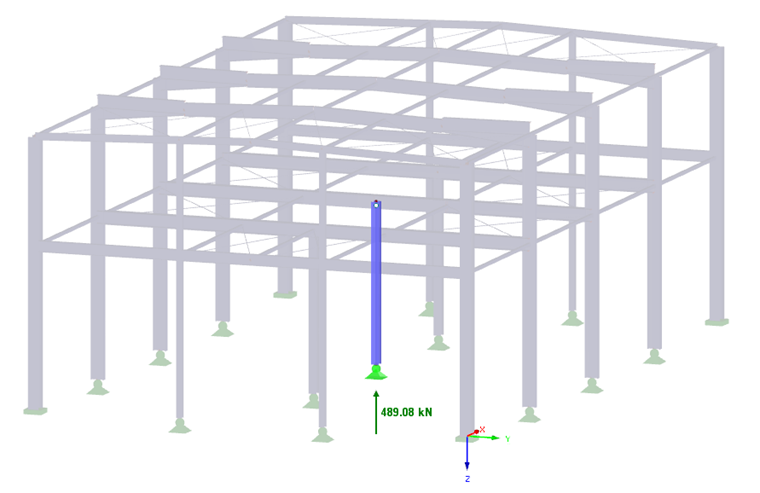
In this example, the calculation of the allowable soil pressure refers to a rectangular foundation plate with dimensions of 1.50 m × 1.50 m × 0.35 m. In the present model, the bearing capacity of a foundation plate of a steel hall is analysed. In the middle of the foundation plate, there is a hinged column of the steel hall, and thus the foundation plate is loaded by the vertical load of V_d = 489.08 kN. Image 03 shows the steel hall column, including the governing support reaction P-Z.

Considered Column of Steel Hall

Determination of Bearing Resistance

The characteristic value of the bearing resistance can be determined for drained conditions according to [1] Appendix D, Equation (D.2):

\frac{R_{k}}{A^{'}} = (c^{'} \cdot N_{c} \cdot b_{c} \cdot s_{c} \cdot i_{c}) + (q^{'} \cdot N_{q} \cdot b_{q} \cdot s_{q} \cdot i_{q}) + (0, 5 \cdot γ^{'} \cdot B^{'} \cdot N_{γ} \cdot b_{γ} \cdot s_{γ} \cdot i_{γ})

Bearing Resistance

In the first step, the effective soil properties are determined initially, as there are two different layers with different soil properties under the foundation base. In this example, the resulting depth of the ground failure cone is z_s = 2.443 m. Thus, Soil 3 is under the foundation base with a depth of 2.443 m − 0.75 m = 1.693 m.

Effective soil properties:

c^{'} = \frac{0, 75 m}{2, 443 m} \cdot 15 kN / m ² + \frac{1, 693 m}{2, 443 m} \cdot 0, 00 kN / m ² = 4, 606 kN / m ²

Effective cohesion

γ' = 20 kN/m³

Effective overburden pressure at the level of the foundation base:
q' = 0.35 m · 20 kN/m³ = 7.0 kN/m²

In the next step, the dimensionless factors for the bearing resistance, the inclination of the foundation base, the shape of the foundation, and the inclination of the load caused by a horizontal load are determined.

Dimensionless factors for bearing resistance:
N_q = e^{π · tanφ'} · tan² (45 + φ' / 2) = 20.096
N_c = (N_q - 1) · cos φ' = 32.069
N_γ = 2 · (N_q - 1) · tan φ' = 22.741

A foundation plate with a square shape is analyzed in this example. Thus, the following dimensionless factors result for the shape of the foundation:
s_q = 1 + sin φ' = 1.512
s_γ = 0.70
s_c = (s_q · N_q - 1) / (N_q - 1) = 1.538

In this context, it should be noted that the effective foundation length L' and the effective foundation width B' must be applied to the foundation dimensions. In this case, only the vertical load is examined and the load eccentricity is equal to zero; thus, the result is L' = B' = 1.50 m and the shape is a "square foundation". If a horizontal load is applied to the foundation, a rectangular effective foundation shape would result from the different effective foundation lengths L' and widths B'.

The resulting dimensionless factors for the inclination of the foundation base b_c, b_q, and b_γ are 1.00, as the bearing resistance design in RF-/FOUNDATION Pro is basically performed for horizontal foundation plates (α = 0°). The resulting dimensionless factors for the inclination of the load caused by a horizontal load H are also 1.00 in this case, since no horizontal loads are applied.

Using these input parameters, we can now determine the ground failure resistance according to (D.2):

\frac{R_{k}}{A^{'}} = (4, 606 \cdot 32, 069 \cdot 1, 538) + (7, 00 \cdot 20, 096 \cdot 1, 512) + (0, 5 \cdot 20 \cdot 1, 50 \cdot 22, 741 \cdot 0, 70) = 678, 66 kN / m ²

allowable characteristic soil pressure

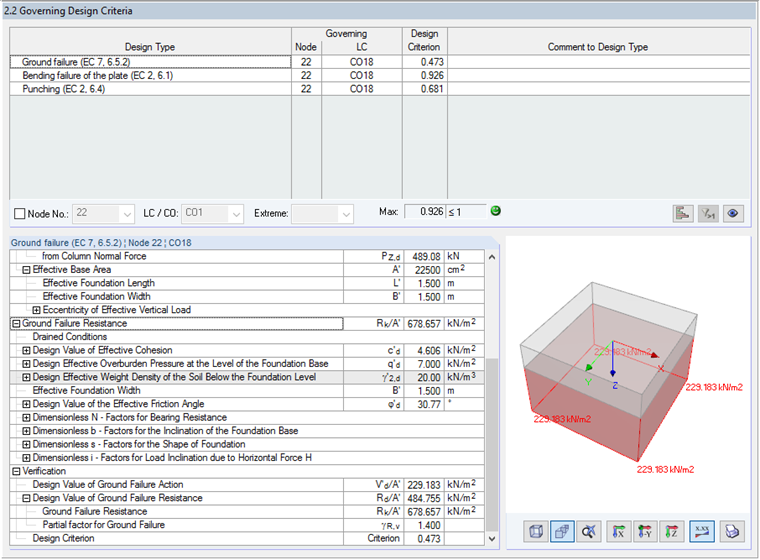
Design Criterion for Ground Failure Resistance

As already mentioned, this example explains the calculation according to CEN using Method 2. Based on the parameters of the National Annex ([1], Table A.5 in this case), the partial factor for ground failure of γ_R,v = 1.4 is provided.

Thus, the design value of the ground failure resistance is:

\frac{R_{d}}{A^{'}} = \frac{678, 66 kN / m ²}{1, 400} = 484, 76 kN / m ²

allowable soil pressure

The existing soil pressure V'_d / A' results from the sum of the stresses due to the axial force in the column and the self-weight of the foundation plate:

\frac{{V^{'}}_{d}}{A^{'}} = \frac{(P_{Z, d} \cdot G_{p, k} \cdot γ_{G, \sup})}{A^{'}} = \frac{(489, 09 kN \cdot 0, 35 m \cdot 1, 50 m \cdot 1, 50 m \cdot 25 kN / m ³ \cdot 1, 35)}{2, 25 m ²} = 229, 18 kN / m ²

Existing soil contact stress

Design criterion:

\frac{{V^{'}}_{d}}{A^{'}} \div \frac{R_{d}}{A^{'}} = \frac{229, 18 kN / m ²}{484, 76 kN / m ²} = 0, 473

Design ratio

Design Criterion in Window 2.2 of RF-/FOUNDATION Pro

You can find more information about the calculation of the ground failure resistance in RF-/FOUNDATION Pro, in the corresponding manual. Chapter 8.4 of the manual also describes the determination of the ground failure resistance. Furthermore, the differences between the analysis methods 2 and 2* are explained here.

References

[1]	EC 7. (2013). Eurocode 7 – Design, Engineering, and Design in Geotechnics - Part 1: General Rules, EN 1997-1:2004 + AC:2009 + A1:2013.

Author

Mr. Kieloch provides technical support to our customers and is responsible for development in the area of reinforced concrete structures.

Links

Downloads

RSTAB Model File

9.01 MB

;