Caso D de exemplos de AIJ - edifício alto no meio de edifícios mais pequenos

Introdução

O Instituto de Arquitectura do Japão (AIJ) apresentou uma série de cenários de referência bem conhecidos para a simulação de vento.
O seguinte artigo trata do "Caso D - Torre entre quarteirões".
A seguir, o cenário descrito é simulado no RWIND2 e os resultados são comparados com resultados simulados e experimentais da AIJ.

Construção do modelo

O caso D descreve um edifício para cuboide simples com uma base quadrada e quatro vezes a altura, rodeado por blocos de apartamentos mais pequenos, também para cubos.
Estes edifícios de apartamentos também têm uma área útil retangular, mas maior, mas apenas um décimo da altura do edifício grande.
O grande edifício central está rodeado pelos blocos de apartamentos mais pequenos num padrão regular.
As dimensões exatas, a velocidade do fluxo e o comportamento na turbulência foram retirados da publicação original [1].
A distribuição da velocidade do fluxo ao longo da altura é apresentada abaixo.

A velocidade do fluxo foi avaliada na simulação em alguns pontos de baixa altitude.
Na experiência de AIJ, foi montado um modelo correspondente num túnel de vento e a velocidade do vento foi medida com sondas de fibra dividida nos pontos mencionados.

Foi utilizado o padrão k – ε como modelo de turbulência e foi assumido um fluxo permanente.
A estrutura do modelo no que diz respeito às dimensões da geometria é apresentada abaixo. A altura de muitos edifícios pequenos é semelhante à da Figura 0.25, enquanto a do edifício central individual é de 2,5.

Layout do modelo - estudo de caso de AIJ: edifício alto rodeado por quarteirões de casas

Configuração do modelo 1 - AIJ caso D

Configuração do modelo 2 - AIJ caso D

A posição dos pontos de medição é resumida na tabela seguinte. Entende-se por origem o piso da cidade no centro de gravidade da área da base do edifício central. Todos os pontos de medição estão a uma altura de 0,05.

Os resultados experimentais da AIJ foram disponibilizados na sua página web [1]. Os dados apresentados da simulação de AIJ foram determinados com a ferramenta ENGAUGE Digitizer [2] a partir dos gráficos da publicação, uma vez que os valores exatos para estes não foram publicados.
No entanto, a precisão dos pontos extraídos deve ser suficientemente precisa (no intervalo de + - 0,5%) e, portanto, facilmente comparável.

No experimento de referência, alguns pontos não foram avaliados, mas foram determinados na simulação. Para não ter que remover completamente esses pontos da avaliação, foi assumido no curso adicional que a experiência e a simulação da literatura fornecem resultados idênticos para esses pontos. Para as seguintes comparações, os resultados da simulação de litro estão até sobrestimados.

Outro fator de influência importante é a configuração "Camadas de fronteira", que aumenta significativamente a densidade da malha em torno da condição de fronteira inferior (solo). No geral, a geração de malhas próximo ao solo influencia mais os resultados nesta região do que seria o caso com uma distância maior ao solo, porque a condição de fronteira do solo tem uma forte influência. Devido à geometria bastante complexa, foi ativada a configuração acima mencionada e o número de camadas extra ("NL") foi definido como 10.

O RWIND Pro 2.02 foi utilizado para este artigo. A estrutura do modelo no RWIND foi adaptada da melhor forma possível à estrutura do CFD de referência.

Ergebnisse e Diskussion

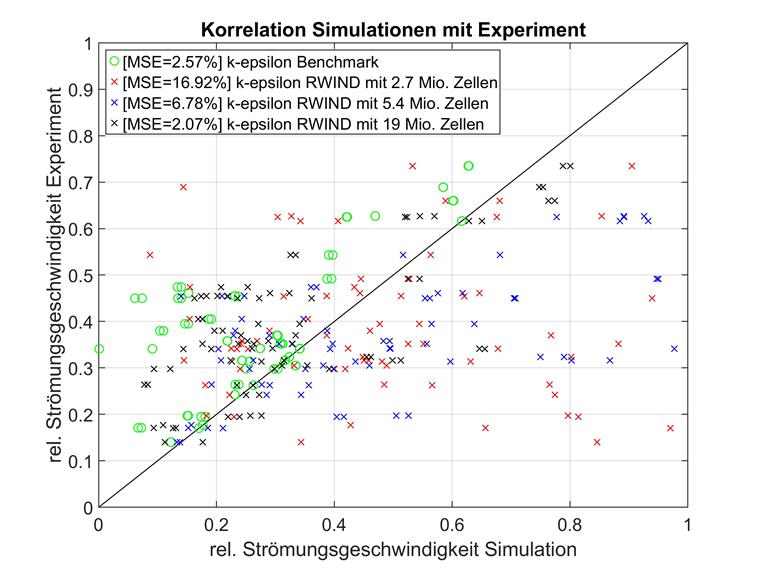
O mapeamento de pontos de medição posicionados tridimensionalmente através de numeração unidimensional simples pode ser difícil de interpretar. Por isso, a seguir, são apresentadas comparações diretas entre a experiência (eixo x) e a simulação (eixo y) para todos os pontos de medição. Quanto mais próximo estiver o ponto de medição da linha diagonal y = x, maior será a correspondência entre a simulação e a experiência. Abaixo estão dois dos modelos RWIND de elementos altos mais adequados, juntamente com o parâmetro de comparação da literatura.

Correlação das simulações com a experiência Simulações de benchmark e RWIND com um grande número de elementos

Imediatamente visível à primeira vista, os resultados dos pontos de medição individuais são distribuídos de forma mais homogênea pelos resultados experimentais. Enquanto a simulação da literatura quase sempre sobrestima a velocidade do fluxo, o RWIND apresenta resultados ora mais baixos, quer mais altos.

O desvio médio quadrado (MSE) foi utilizado como critério de comparação, mas uma comparação dos coeficientes de determinação também mostraria o mesmo comportamento, por exemplo. Foi preferido o quadrado do desvio médio ao coeficiente de determinação porque a relação entre as velocidades do fluxo experimental e simulada não representa uma regressão e, portanto, significaria apenas um tipo de ponderação dos desvios individuais e nenhuma qualidade de ajuste. O MSE é geometricamente mais fácil de interpretar com a mesma expressividade.

O critério de comparação MSE confirma a presunção da primeira observação. Ambos os modelos com alta resolução de malha mas diferentes modelos de turbulência cumprem muito bem a referência experimental. O modelo k-epsilon é ainda melhor do que o da publicação, enquanto o modelo k-omega fica logo atrás.

No entanto, não deve ser esquecido que vários pontos para o benchmark da literatura foram artificialmente assumidos como sem falhas.
Se estes pontos forem calculados para o MSE, ambos os modelos do RWIND apresentarão um erro menor do que o valor de referência.

É aconselhável observar mais de perto a influência da densidade da malha. A seguir, redes de diferentes densidades com uma estrutura de modelo idêntica e um modelo de turbulência RAS k-épsilon são comparadas com o parâmetro de referência da literatura. Os resultados são apresentados abaixo.

Correlação das simulações com a experiência Simulações de benchmark e do RWIND k-epsilon com diferentes números de elementos

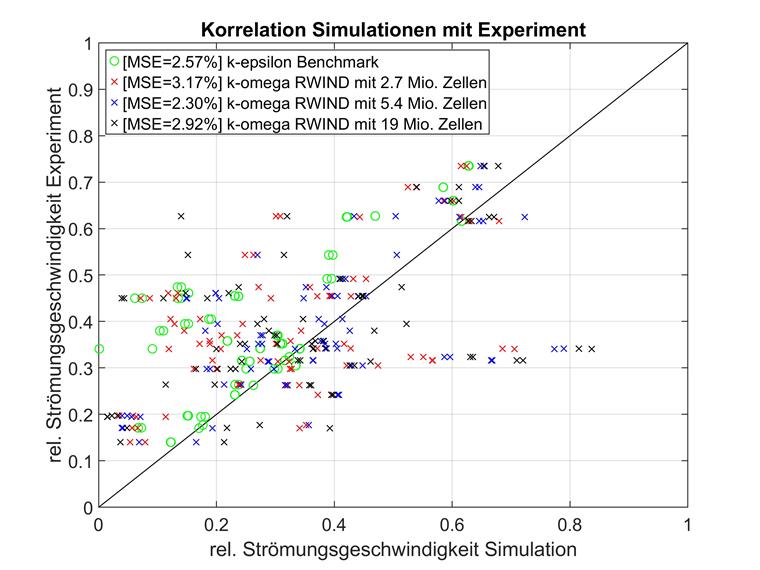
Também foi realizado um estudo de convergência de rede para o modelo de turbulência k-omega e as mesmas formações de rede. Os resultados são apresentados abaixo.

Correlação das simulações com a experiência Simulações de benchmark e RWIND k-omega com diferentes números de elementos

Enquanto o modelo de turbulência k-epsilon RAS pode alcançar resultados ligeiramente melhores para um número muito alto de elementos, o desvio quadrado médio nos modelos k-omega converge muito mais rapidamente com o aumento da densidade da malha. O melhor exemplo é o par de modelos com 2,7 milhões de células. Aqui, o modelo k-epsilon é completamente inútil, enquanto o k-omega pode já proporcionar bons resultados.
De fato, o modelo k-omega de resolução média obtém a melhor concordância com o experimento e também pode ter um desempenho superior aos modelos RWIND de resolução significativamente mais alta. Não foi possível identificar uma razão precisa para isso. Um problema de otimização com uma dimensionalidade tão alta pode, portanto, ser assumido como um problema de acerto casual.

Para uma comparação mais clara da simulação de referência com os resultados do RWIND, é aconselhável considerar as velocidades de fluxo como uma imagem a cores de garrafa. A secção considerada em torno do edifício foi adaptada à dos autores [1]. Por razões de direitos de autor, as imagens a cores falsas não são comparadas lado a lado neste momento. O resultado é apresentado abaixo.

Velocidade do fluxo sobre todos os edifícios - AIJ caso D

Aqui, também, existe uma concordância muito boa com a simulação da literatura. Não existem desvios significativos nem áreas visíveis.

No geral, k-omega é sempre mais preciso para modelos de resolução mais baixa para este estudo de caso, enquanto os resultados com alta densidade de malha ainda são muito bons.
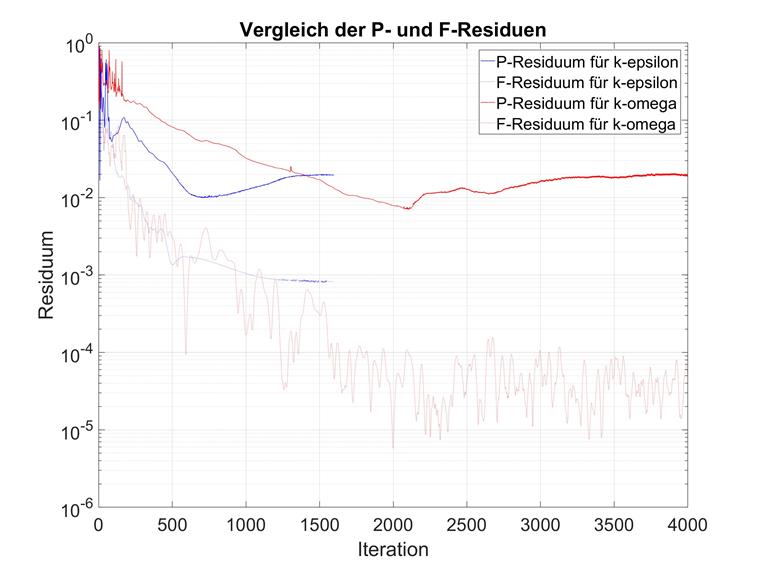
Por outro lado, o residual de pressão nos modelos k-omega converge após significativamente mais iterações. Uma comparação é apresentada abaixo.

Resíduos para dois modelos de turbulência

As presentes observações coincidem com as expectativas dos diferentes modelos de turbulência. Para a utilização do k-omega, é portanto aconselhável aumentar consideravelmente o número de iterações máximas. O valor predefinido de 300 deveria ser aumentado manualmente para pelo menos 1000.

Resumo

Os desvios quadrados médios de várias combinações de número de elementos e modelo de turbulência são resumidos abaixo.

Uma possível abordagem de melhoria é geralmente um refinamento da malha. No entanto, no caso deste modelo, a influência de tal refinamento de malha é muito pequena. A configuração "Camadas de fronteira" já representa um refinamento da malha, para que os edifícios circundantes relativamente pequenos devem ser suficientemente discretizados. Uma investigação de densificação da rede foi dispensada após a avaliação de um modelo de teste.

Por fim, existe uma concordância muito boa entre o RWIND e o valor de referência experimental, que pode até superar o valor de referência da literatura. Ambos os modelos de turbulência são adequados para isso, pelo que o k-omega pode apresentar resultados significativamente melhores para baixas densidades de rede.

[1] https://www.aij.or.jp/jpn/publish/cfdguide/
[2] https://markummitchell.github.io/engauge-digitizer/

• Visualizador 3D | Google
• Visualizador 3D | Babylon
• Realidade virtual

177x

4x

Exemplo D do AIJ Bechmarks - edifício alto rodeado por blocos de casas (uniformes)