Wstęp
Japoński Instytut Architektury (AIJ) przedstawił kilka dobrze znanych scenariuszy odniesienia dla symulacji wiatru.
Poniższy artykuł dotyczy „Przypadku D – Wieżowiec wśród bloków miejskich”.
W poniższym tekście opisany scenariusz jest symulowany w RWIND 2, a wyniki są porównywane z wynikami symulacji i eksperymentów przez AIJ.
Układ modelu
Przypadek D opisuje prosty budynek w kształcie prostopadłościanu o podstawie kwadratu i cztery razy większej, otoczony mniejszymi blokami mieszkalnymi, które również są prostopadłościenne.
Te budynki mieszkalne również mają prostokątną, ale większą powierzchnię, jednak stanowiącą zaledwie jedną dziesiątą wysokości dużego budynku.
Duży, centralny budynek otoczony jest mniejszymi blokami mieszkalnymi.
Dokładne wymiary, prędkość przepływu i zachowanie w stanie turbulencji zaczerpnięto z oryginalnej publikacji [1].
Poniżej pokazano rozkład prędkości przepływu na wysokości.
| Wysokość w m | Prędkość przepływu w m/s | |
|---|---|---|
| 1 | 0.005 | 0,576 |
| 2 | 0,010 | 0,620 |
| 3 | 0,020 | 0,650 |
| 4 | 0,030 | 0,673 |
| 5 | 0,050 | 0,713 |
| 6 | 0,100 | 0,800 |
| 7 | 0,200 | 0,945 |
| 8 | 0,300 | 1,050 |
| 9 | 0,400 | 1,135 |
| 10 | 0,600 | 1.305 |
| 11 | 0,800 | 1,432 |
| 12 | 1,000 | 1,507 |
| 13 | 1,200 | 1,514 |
W symulacji oszacowano prędkość przepływu w kilku punktach na małej wysokości.
W eksperymencie z AIJ, odpowiedni model ustawiono w tunelu aerodynamicznym, a prędkość wiatru mierzono we wspomnianych punktach za pomocą sond z włókna szklanego.
Jako model turbulencji zastosowano standardową k–ε przy założeniu, że przepływ jest stały.
Poniżej pokazano konstrukcję modelu z uwzględnieniem wymiarów geometrii. Wysokość małych budynków jest zbliżona do Rysunek& 0,25, podczas gdy wysokość pojedynczego budynku centralnego wynosi 2,5.
Położenie punktów pomiarowych podsumowano w poniższej tabeli. Pochodzenie rozumiane jest jako podłoże miejskie w środku ciężkości podstawy budynku centralnego. Wszystkie punkty pomiarowe znajdują się na wysokości 0,05.
| Współrzędna x | Współrzędna y | Punkt | Współrzędna x | Współrzędna y | Punkt | Współrzędna x | Współrzędna y | |
|---|---|---|---|---|---|---|---|---|
| 1 | -137.5 | 62.5 | 27 | -37.5 | 12.5 | 53 | 62.5 | -87.5 |
| 2 | -137.5 | -62.5 | 28 | -37.5 | -12.5 | 54 | 62.5 | -112.5 |
| 3 | -112.5 | 62.5 | 29 | -37.5 | -37.5 | 55 | 87,5 | 112,5 |
| 4 | -112.5 | -62.5 | 30 | -37.5 | -62.5 | 56 | 87,5 | 87,5 |
| 5 | -87.5 | 112,5 | 31 | -12.5 | 62.5 | 57 | 87,5 | 62.5 |
| 6 | -87.5 | 87,5 | 32 | -12.5 | 37.5 | 58 | 87,5 | 37.5 |
| 7 | -87.5 | 62.5 | 33 | -12.5 | -37.5 | 59 | 87,5 | 12.5 |
| 8 | -87.5 | 37.5 | 34 | -12.5 | -62.5 | 60 | 87.5 | -12.5 |
| 9 | -87.5 | 12.5 | 35 | 12.5 | 62.5 | 61 | 87.5 | -37.5 |
| 10 | -87.5 | -12.5 | 36 | 12.5 | 37.5 | 62 | 87.5 | -62.5 |
| 11 | -87.5 | -37.5 | 37 | 12.5 | -37.5 | 63 | 87.5 | -87.5 |
| 12 | -87.5 | -62.5 | 38 | 12.5 | -62.5 | 64 | 87.5 | -112.5 |
| 13 | -87.5 | -87.5 | 39 | 37.5 | 62.5 | 65 | 112,5 | 112,5 |
| 14 | -87.5 | -112.5 | 40 | 37.5 | 37.5 | 66 | 112,5 | 87,5 |
| 15 | -62.5 | 112,5 | 41 | 37.5 | 12.5 | 67 | 112,5 | 62.5 |
| 16 | -62.5 | 87,5 | 42 | 37.5 | -12.5 | 68 | 112,5 | 37.5 |
| 17 | -62.5 | 62.5 | 43 | 37.5 | -37.5 | 69 | 112,5 | 12.5 |
| 18 | -62.5 | 37.5 | 44 | 37.5 | -62.5 | 70 | 112.5 | -12.5 |
| 19 | -62.5 | 12.5 | 45 | 62.5 | 112,5 | 71 | 112.5 | -37.5 |
| 20 | -62.5 | -12.5 | 46 | 62.5 | 87,5 | 72 | 112.5 | -62.5 |
| 21 | -62.5 | -37.5 | 47 | 62.5 | 62.5 | 73 | 112.5 | -87.5 |
| 22 | -62.5 | -62.5 | 48 | 62.5 | 37.5 | 74 | 112.5 | -112.5 |
| 23 | -62.5 | -87.5 | 49 | 62.5 | 12.5 | 75 | 137,5 | 62.5 |
| 24 | -62.5 | -112.5 | 50 | 62.5 | -12.5 | 76 | 137.5 | -62.5 |
| 25 | -37.5 | 62.5 | 51 | 62.5 | -37.5 | 77 | 162,5 | 62.5 |
| 26 | -37.5 | 37.5 | 52 | 62.5 | -62.5 | 78 | 162.5 | -62.5 |
Wyniki eksperymentalne AIJ zostały opublikowane na ich stronie internetowej [1]. Wyświetlane dane symulacji AIJ zostały określone za pomocą programu ENGAUGE Digitizer [2] na podstawie wykresów opublikowanych w publikacji [1], ponieważ dokładne wartości nie zostały opublikowane.
Dokładność wyodrębnionych punktów powinna być jednak wystarczająco dokładna (w zakresie +-0,5%), a zatem łatwo porównywalna.
W eksperymencie wzorcowym niektóre punkty nie zostały ocenione, ale zostały wyznaczone w symulacji. Aby uniknąć konieczności całkowitego wyłączania tych punktów z oceny, założono, że eksperyment i symulacja literaturowa dają dla tych punktów identyczne wyniki. W przypadku poniższych porównań wyniki symulacji literaturowej są nawet zawyżone.
Innym ważnym czynnikiem jest ustawienie „Warstwy graniczne”, które znacznie zwiększa gęstość siatki wokół dolnej granicy warunku (grunt). Ogólnie rzecz biorąc, siatkowanie w pobliżu gruntu wpływa na wyniki w tym obszarze w większym stopniu niż w przypadku większej odległości od gruntu, ponieważ warunek brzegowy gruntu ma duży wpływ. Ze względu na dość złożoną geometrię miasta aktywowano wspomniane ustawienie, a liczba dodatkowych warstw („NL”) została ustawiona na 10.
W artykule wykorzystano program RWIND Pro 2.02. Struktura modelu w RWIND została dostosowana w możliwie największym stopniu do struktury CFD odniesienia.
Wyniki i dyskusja
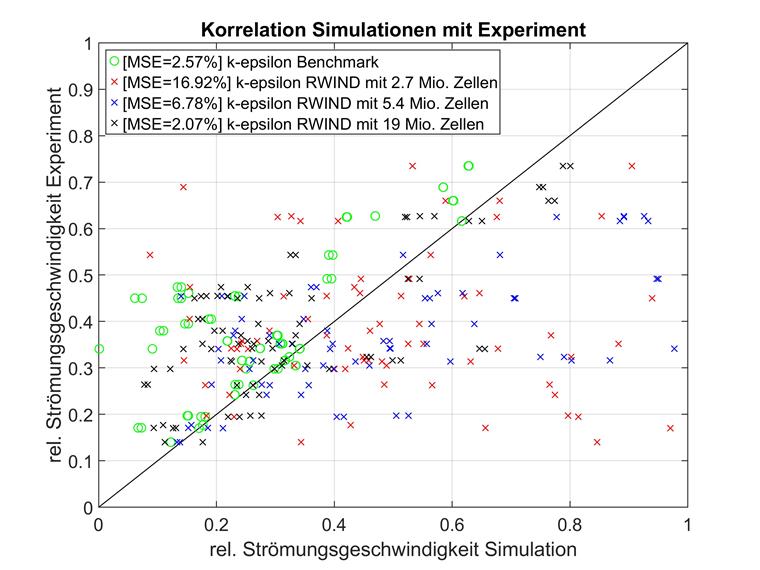
Punkty pomiarowe umieszczone w przestrzeni trójwymiarowej przedstawione za pomocą prostej jednowymiarowej numeracji mogą być trudne do zinterpretowania. Dlatego poniżej pokazano bezpośrednie porównanie eksperymentu (oś x) i symulacji (oś y) dla wszystkich punktów pomiarowych. Im bliżej linii ukośnej y=x znajduje się punkt pomiarowy, tym większa jest korelacja między symulacją a eksperymentem. Poniżej przedstawiamy dwa najlepiej dopasowane modele wysokoelementowe RWIND wraz z benchmarkiem z literatury.
Na pierwszy rzut oka widać, że wyniki poszczególnych punktów pomiarowych są bardziej równomiernie rozłożone wokół wyników eksperymentalnych. Podczas gdy symulacja literaturowa prawie zawsze zawyża prędkość przepływu, RWIND pokazuje czasem niższe, a czasem wyższe wyniki.
Jako kryterium porównawcze zastosowano odchylenie średniokwadratowe (MSD), ale na przykład porównanie współczynników determinacji wykazałoby takie samo zachowanie. Preferowano średnią odchyłkę kwadratową od współczynnika determinacji, ponieważ stosunek prędkości eksperymentalnej i symulowanej nie stanowi regresji, a zatem byłby tylko rodzajem ważenia poszczególnych odchyleń, a nie wartością dopasowania. MSD jest geometrycznie łatwiejszy do interpretacji z taką samą wyrazistością.
Kryterium porównania MSD potwierdza przypuszczenie zawarte w pierwszej obserwacji. Oba modele o wysokiej rozdzielczości siatki, ale różne modele turbulencji, bardzo dobrze spełniają kryteria eksperymentalne. Model k-epsilon jest nawet lepszy niż w publikacji, podczas gdy model k-omega jest niewiele w tyle.
Nie należy jednak zapominać, że kilka punktów odniesienia dla literatury zostało sztucznie przyjętych jako błędne.
Jeżeli punkty te zostaną obliczone dla MSD, oba modele RWIND wykazują mniejszy błąd niż wartość odniesienia.
Zaleca się przyjrzenie się wpływowi gęstości siatki. Poniżej porównano siatki o różnych gęstościach z identyczną konstrukcją modelu oraz modelem turbulencji k-epsilon RAS z modelem literaturowym. Wyniki pokazano poniżej.
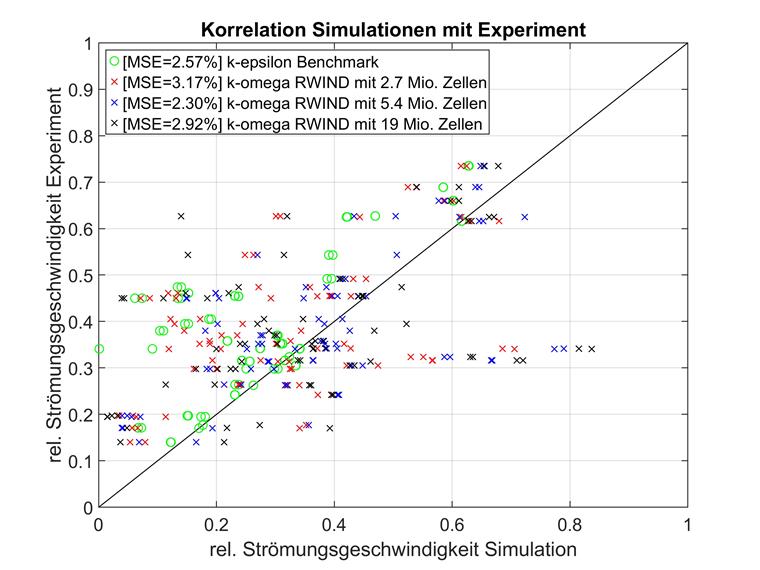
Przeprowadzono również badanie zbieżności siatki dla modelu turbulencji k-omega i tych samych formacji siatki. Wyniki pokazano poniżej.
Podczas gdy model turbulencji k-epsilon RAS może osiągnąć nieco lepsze wyniki w przypadku bardzo dużej liczby pierwiastków, średnie odchylenie kwadratowe w modelach k-omega osiąga zbieżność znacznie szybciej wraz ze wzrostem gęstości siatki. Najlepszym tego przykładem jest para modeli z 2,7 milionami komórek. Tutaj model k-epsilon jest zupełnie bezużyteczny, podczas gdy k-omega może już dostarczyć dobrych wyników.
W rzeczywistości model k-omega o średniej rozdzielczości jest w najlepszym razie zgodny z eksperymentem, a także może przewyższyć modele RWIND o znacznie wyższej rozdzielczości. Nie udało się określić dokładnej przyczyny. Można zatem założyć, że problem optymalizacji przy tak dużej wymiarowości jest przypadkowy.
Aby lepiej porównać symulację referencyjną z wynikami RWIND, zaleca się wyświetlić prędkości przepływu jako kolorowy obraz butelki. Przekrój wokół rozpatrywanego budynku został dostosowany do przekroju autorów [1]. Ze względu na ochronę praw autorskich obrazy w kolorze sztucznym nie są tu porównywane obok siebie. Wynik pokazano poniżej.
Istnieje również bardzo dobra korelacja z symulacją literaturową. Brak znaczących odchyleń lub zauważalnych obszarów.
Podsumowując, w tym studium przypadku, k-omega jest zawsze bardziej dokładna dla modeli o niższej rozdzielczości, podczas gdy wyniki z dużą gęstością siatki są nadal bardzo dobre.
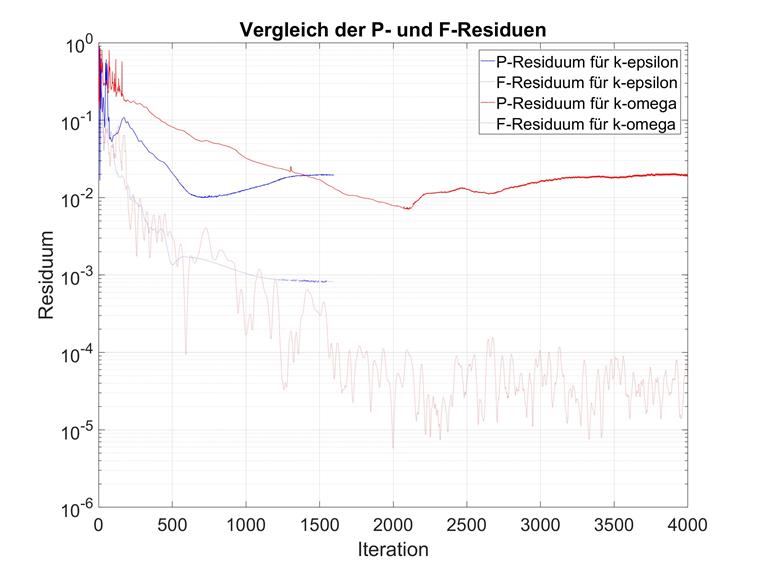
Z drugiej strony, ciśnienie rezydualne w modelach k-omega jest zbieżne po znacznie większej liczbie iteracji. Porównanie pokazano poniżej.
Obserwacje te są zbieżne z oczekiwaniami dotyczącymi różnych modeli turbulencji. Aby zastosować k-omega, zalecamy znaczne zwiększenie liczby maksymalnych iteracji. Domyślną wartość 300 należy ręcznie zwiększyć do co najmniej 1000.
Uwagi końcowe
Poniżej zestawiono średnie odchylenia kwadratowe dla różnych kombinacji numeru elementu i modelu turbulencji.
| Model turbulencji k-epsilon | Model turbulencji k-omega | |
|---|---|---|
| Odniesienie | 2,57% | nie dotyczy |
| 2,7 miliona komórek | 16,92% | 3,17% |
| 5,4 miliona komórek | 6,78% | 2,30% |
| 19 milionów komórek | 2,07% | 2,92% |
Możliwym podejściem ulepszeń jest często zagęszczenie siatki. W przypadku tego modelu wpływ takiego zagęszczenia siatki jest jednak bardzo mały. Ustawienie „Warstwy graniczne” już odzwierciedla zagęszczenie siatki, dzięki czemu można wystarczająco zdyskretyzować stosunkowo niewielkie budynki w sąsiedztwie. Po dokonaniu oceny modelu testowego zrezygnowano z analizy zagęszczania siatki.
Wreszcie, istnieje bardzo dobra zgodność między RWIND a wzorcem eksperymentalnym, który może nawet przewyższyć wzorce dostępne w literaturze. Obydwa modele turbulencji są do tego odpowiednie, dzięki czemu k-omega może zapewnić znacznie lepsze wyniki dla małych gęstości siatki.
[1]
Poradnik dla prognoz CFD dla wiatru w miastach
[2]
Zaangażuj digitizera