项目介绍
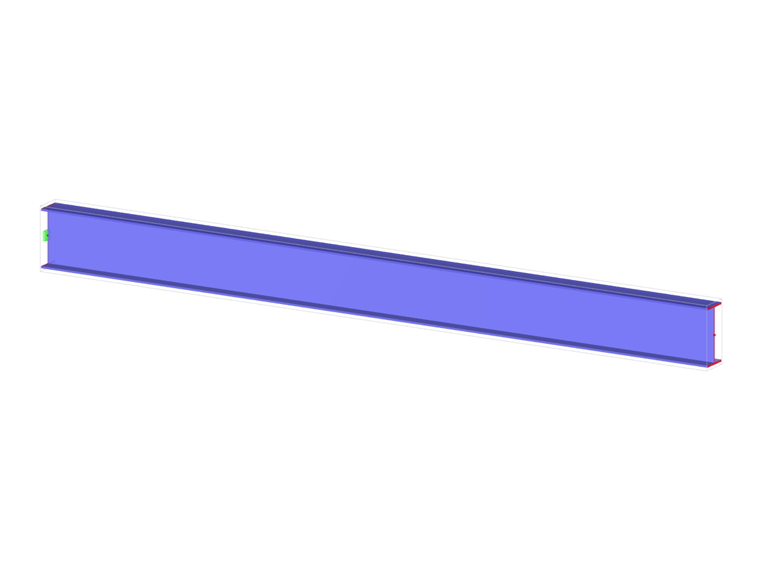
左端 (x=0) 支承为 I 形截面的悬臂梁,悬臂梁的支承扭矩 M 为 sketch。 本例的目的是对固定式支座和货叉式支座进行比较,并研究一些有代表性的问题的行为。 并与通过板的解决方案进行了比较。 验算示例是基于 Gensichen 和 Lumpe 提出的示例(参见参考资料)。 该模型考虑了小变形,并忽略了自重。 计算一半悬臂的旋转 φx (L/2) ,如果杆件实体存在翘曲,则计算主扭矩 MTpri ,次扭矩 MTsec和翘曲弯矩 Mω左端(点 A)和右端(点 B)。 下面的参数集描述了该问题。
| 材料 | 钢 | 弹性模量 | E | 210000,000 | MPa |
| 剪切模量 | G | 81000,000 | MPa | ||
| 几何尺寸 | 悬臂 | 周长 | l | 5,000 | m |
| 截面 | 高度 | h | 400,000 | mm | |
| 宽度 | b | 180,000 | mm | ||
| 腹板厚度 | S | 10,000 | mm | ||
| 翼缘厚度 | t | 14,000 | mm | ||
| 荷载 | 弯矩 | M | 1,000 | kNm | |
解析解
在计算翘曲翘曲的杆件时,总扭矩 MT分为主扭矩 MTpri和次扭矩 MTsec 。
计算公式如下:
完整的扭矩微分方程。 可以采用求解初始参数的方法,将其求解出转动 φx 、相对扭转 φ' ,以及翘曲弯矩 Mω ,主扭矩 MTpri和从扭矩 MTsec 。
当考虑固定支座时,翘曲被约束。 此时的边界条件为: φ(0)=0,φ'(0)=0,MT (0)=M,Mω (L)=0。
考虑货叉支座翘曲,边界条件如下: φ(0)=0,Mω (0)=0,MT (0)=M,Mω (L)=0。
使用这些边界条件,旋转 φ(x) 的结果进入著名的公式。
RFEM 设置
- 在 RFEM 5.05 和 RFEM 6.01 中建模
- 单元尺寸 lFE = 0.025 m
- 使用各向同性线弹性材料模型
- 使用 Kirchhoff 板弯曲理论
- 在 RFEM 6 中使用的翘曲扭转和钢结构设计模块
结果
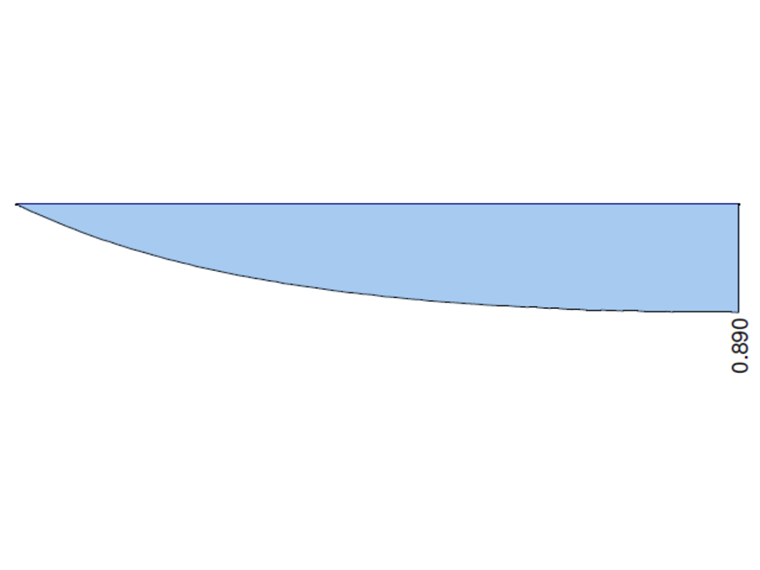
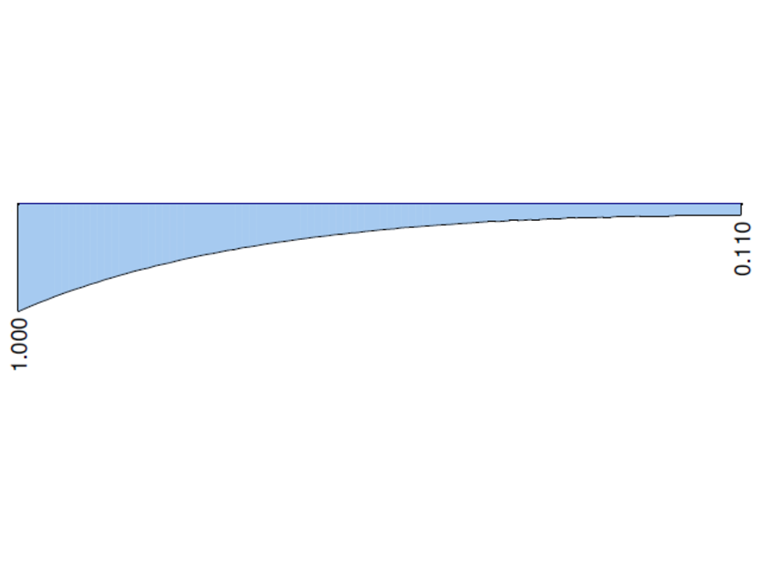
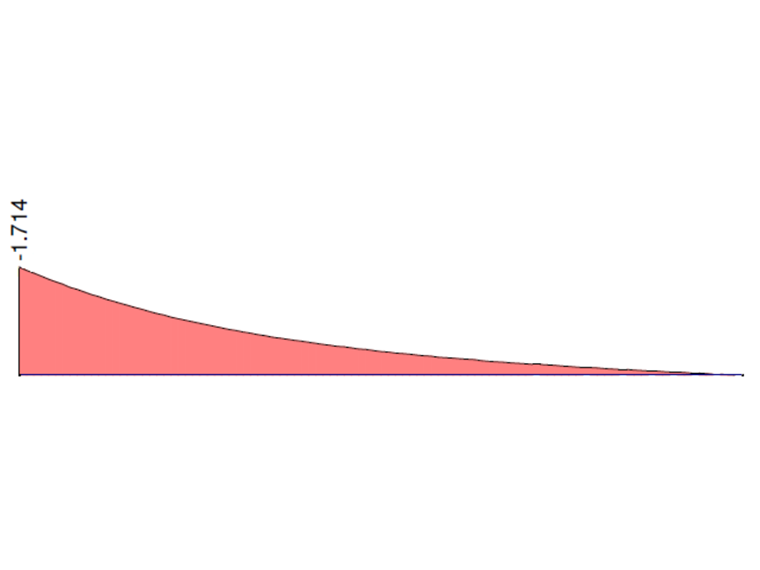
下面的曲线图显示了在 RFEM 6 和 5 中计算的总扭矩 MT 、主扭矩 MTpri 、次扭矩 MTsec和翘曲弯矩 Mω的特性曲线,当考虑固定支座时, 将悬臂梁两端的数值与解析解和 ANSYS 13 中的解进行比较。
| 解析解 | ANSYS 13 | 比值 | RFEM 6 | 比值 | RFEM RF-FE-LTB | 比值 | |
| MTpri [kNm] | 0,000 | 0,008 | <现在wiki>- | 0,000 | <现在wiki>- | 0,000 | <现在wiki>- |
| MTsec [kNm] | 1,000 | 0,992 | 0,992 | 1,000 | 1,000 | 1,000 | 1,000 |
| Mω [kNm] | -1.714 | -1.683 | 0,989 | -1.743 | 1,017 | -1.714 | 1,000 |
| 解析解 | ANSYS 13 | 比值 | RFEM 6 | 比值 | RFEM RF-FE-LTB | 比值 | |
| MTpri [kNm] | 0,890 | 0,893 | 1,003 | 0,869 | 0,976 | 0,890 | 1,000 |
| MTsec [kNm] | 0,110 | 0,107 | 0,973 | 0,131 | 1,191 | 0,110 | 1,000 |
| Mω [kNm] | 0,000 | 0,001 | <现在wiki>- | 0,000 | <现在wiki>- | 0,000 | <现在wiki>- |
可以将绕 x 轴转动的计算结果与考虑货叉支座和板模型的结果进行比较, 对于板模型,由于受影响的区域在加载点附近,所以使用二分之一长度 φ(L/2) 处的旋转。 对于板模型,货叉支座的定义比较复杂,因为翘曲弯矩必须为零。 该边界条件不能在 RFEM 5/RFEM 6 中直接设置。 所使用的近似值如下面的 [[]] #fig 图]] 所示。 支座的所有边缘上绕 x 轴的旋转都被约束。 只有中心节点(在轴上)是完全固定的。 当支座为固定支座时,支座的所有边都是固定的。
| 支座 | ANSYS 13 | RFEM 6 (杆件) | RFEM 6(板) | ||||
| φx (L/2) [mrad] | φx (L/2) [mrad] | 比值 [-] | φx (L/2) [mrad] | 比值 [-] | φx (L/2) [mrad] | 比值 [-] | |
| 固定支座 | 32,6 | 32,2 | 0.988 | 32,4 | 0,994 | 32,7 | 1,003 |
| 货叉支座 | 69,9 | 68,5 | 0.979 | 69.9 | 1,000 | 68,8 | 0,999 |
| 支座 | ANSYS 13 | RFEM 5、RF-FE-LTB(杆件) | RFEM 5(板) | ||||
| φx (L/2) [mrad] | φx (L/2) [mrad] | 比值 [-] | φx (L/2) [mrad] | 比值 [-] | φx (L/2) [mrad] | 比值 [-] | |
| 固定支座 | 32,6 | 32,2 | 0.988 | 32,6 | 1,000 | 32.5 | 0,974 |
| 货叉支座 | 69,9 | 68,5 | 0.979 | 69,9 | 1,000 | 68,1 | 0,974 |
备注 1: 这里使用板模型的解决方案来说明翘曲效应。 产生相对误差的另一个原因是货叉支座的近似值。
备注 2: Designtec sro 公司在 ANSYS 13 中进行了数值求解 这里的 MTpri和 $ MTsec不是 ANSYS 13 的原始结果。 由翘曲弯矩 Mω计算得出。 因此它们不能作为完全精确的数值。 单元 BEAM188 用于 ANSYS 13 。