Beschreibung
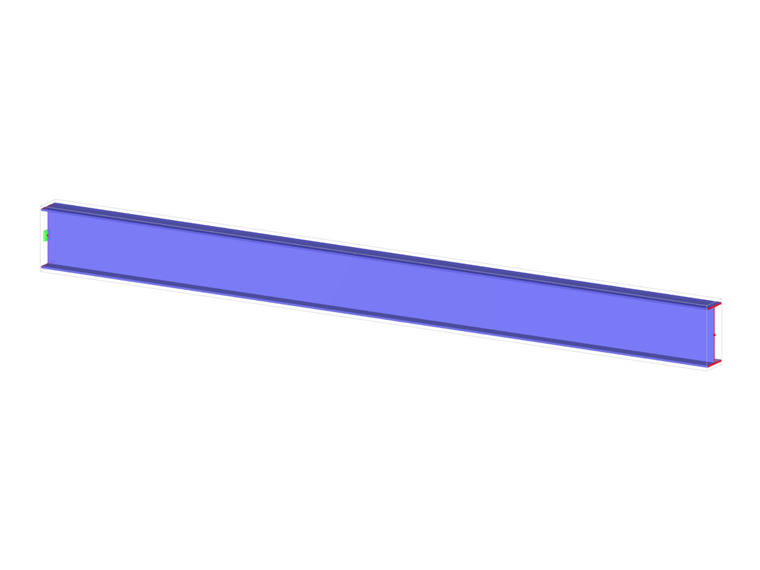
Ein Kragträger mit I-Profil ist am linken Ende gelagert (x=0) und wird durch das Drehmoment M gemäß folgendem sketch belastet. Ziel dieses Beispiels ist es, das feste Lager mit dem Gabellager zu vergleichen und das Verhalten einiger repräsentativer Größen zu untersuchen. Der Vergleich mit der Lösung mittels Platten wird ebenfalls durchgeführt. Dieses Verifikationsbeispiel basiert auf dem von Gensichen und Lumpe vorgestellten Beispiel (siehe Literatur). Es werden kleine Verformungen berücksichtigt und das Eigengewicht wird vernachlässigt. Es soll die Verdrehung in der Hälfte des Kragträgers φx (L/2) bestimmt werden und im Falle der Stabentität mit Verwölbung die Werte des primären Torsionsmomentes MTpri, des sekundären Torsionsmomentes MTsec und des Wölbmomentes Mω beide an am linken Ende (Punkt A) und am rechten Ende (Punkt B). Das Problem wird durch folgenden Parametersatz beschrieben.
| Material | Stahl | Elastizitätsmodul | E | 210000,000 | MPa |
| Schubmodul | G | 81000,000 | MPa | ||
| Geometrie | Kragarm | Länge | L | 5,000 | m |
| Querschnitt | Höhe | h | 400,000 | mm | |
| Breite | F | 180,000 | mm | ||
| Stegdicke | S | 10,000 | mm | ||
| Flanschdicke | t | 14,000 | mm | ||
| Last | Moment | M | 1,000 | kNm | |
Analytische Lösung
Bei der Berücksichtigung einer Stabberechnung mit Verwölbung wird das Gesamttorsionsmoment MT zwischen dem primären Torsionsmoment MTpri und dem sekundären Torsionsmoment MTsec aufgeteilt.
Die Gleichung kann wie folgt formuliert werden:
Das ist die vollständige Differentialgleichung der Torsion. Dieses lässt sich nach der Methode der Anfangsparameter lösen und ergibt Gleichungen für die Rotation φx, die relative Verdrehung φ'x und das Wölbmoment Mω, das primäre Torsionsmoment MTpri und das sekundäre Torsionsmoment MTsec.
Die Verwölbung wird behindert, wenn die feste Einspannung berücksichtigt wird. Randbedingungen sind in diesem Fall: φ(0)=0, φ'(0)=0, MT (0)=M, Mω (L)=0.
Wenn die Gabellagerung berücksichtigt wird, ist die Wölbung aktiviert und es gelten folgende Randbedingungen: φ(0)=0,Mω (0)=0, MT (0)=M, Mω (L)=0.
Mit diesen Randbedingungen ergibt sich die Verdrehung φ(x) in die bekannte Formel.
RFEM-Einstellungen
- Modelliert in RFEM 5.05 und RFEM 6.01.
- Die Elementgröße beträgt lFE = 0,025 m
- Es wird ein isotropes linear-elastisches Materialmodell vorausgesetzt.
- Kirchhoff die Plattenbiegetheorie
- In RFEM 6 wird das Add-on Wölbkrafttorsion und Stahlbemessung verwendet
Ergebnisse
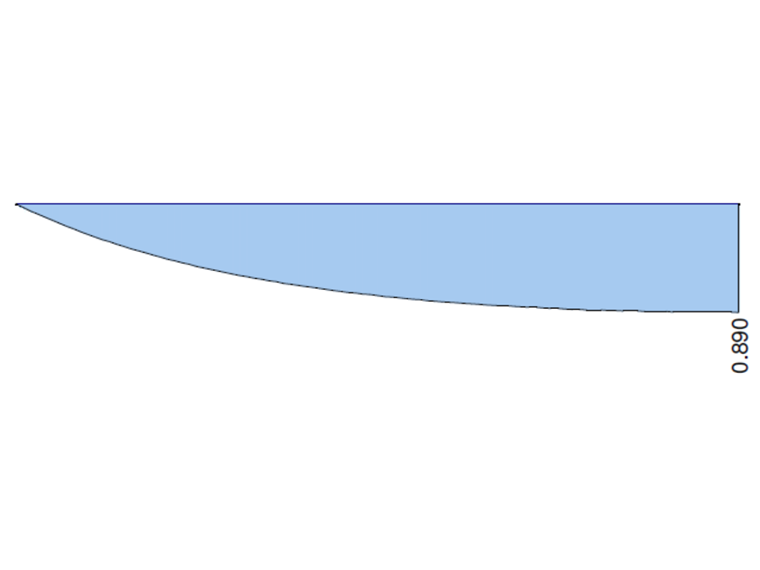
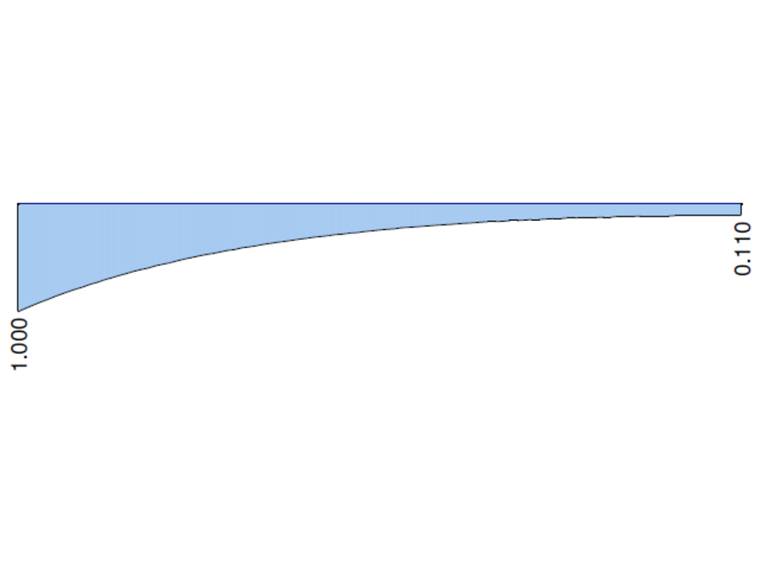
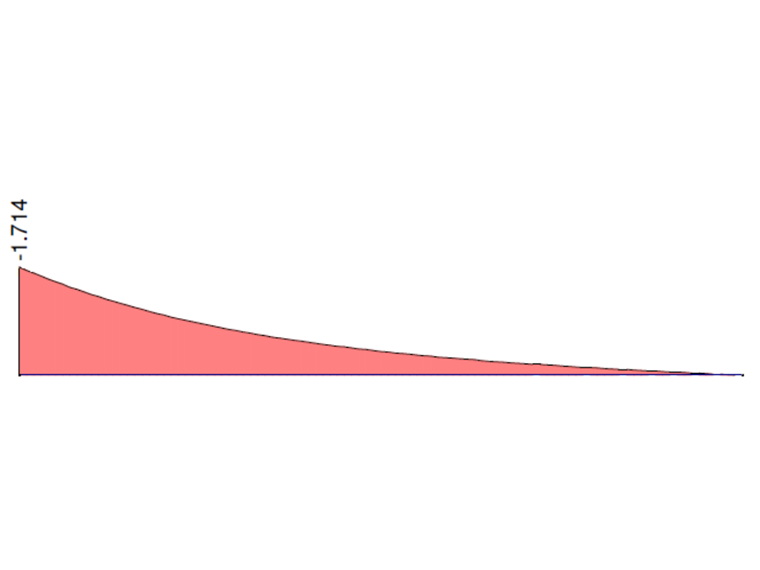
Die folgenden Grafiken stellen die Verläufe des Gesamttorsionsmoments MT, des primären Torsionsmoments MTpri, des sekundären Torsionsmoments MTsec und des Wölbkraftmoments Mω dar, berechnet in RFEM 6 und RFEM 5, Modul RF-FE-BGDK. die feste Einspannung berücksichtigt wird. Die Werte an beiden Enden des Kragarms werden mit der analytischen Lösung und der Lösung in ANSYS 13 verglichen.
| Punkt A (x=0) | Analytische Lösung | ANSYS 13 | Verhältnis | RFEM 6 | Verhältnis | RFEM RF-FE-BGDK | Verhältnis |
| MTpri [kNm] | 0,000 | 0,008 | |||||
| 0,000 | |||||||
| 0,000 | |||||||
| MTsec [kNm] | 1,000 | 0,992 | 0,992 | 1,000 | 1,000 | 1,000 | 1,000 |
| Mω [kNm] | -1.714 | -1,683 | 0,989 | -1.743 | 1,017 | -1.714 | 1,000 |
| Punkt B (x=L) | Analytische Lösung | ANSYS 13 | Verhältnis | RFEM 6 | Verhältnis | RFEM RF-FE-BGDK | Verhältnis |
| MTpri [kNm] | 0,890 | 0,893 | 1,003 | 0,869 | 0,976 | 0,890 | 1,000 |
| MTsec [kNm] | 0,110 | 0,107 | 0,973 | 0,131 | 1,191 | 0,110 | 1,000 |
| Mω [kNm] | 0,000 | 0,001 | |||||
| 0,000 | |||||||
| 0,000 |
Die berechnete Verdrehung um die x-Achse kann mit den Ergebnissen verglichen werden, wenn die Gabellagerung berücksichtigt wird, und auch mit Plattenmodellen, bei denen die Verwölbung natürlich berücksichtigt wird. Die Verdrehung um die halbe Länge φ(L/2) wird bei Plattenmodellen aufgrund des betroffenen Bereichs in der Nähe des Belastungspunktes verwendet. Die Definition der Gabellagerung beim Plattenmodell ist kompliziert, da das Wölbmoment gleich null sein muss. Diese Randbedingung kann nicht direkt in RFEM 5/RFEM 6 eingestellt werden. Die verwendete Näherung ist im folgenden Bild dargestellt. An allen Rändern des Lagers wird die Verdrehung um die x-Achse behindert. Vollständig fixiert ist nur der mittlere Knoten (an der Achse). Bei einer festen Stützung sind alle Ränder des Auflagers fest.
| Lagerung | Analytische Lösung | ANSYS 13 | RFEM 6 (Stab) | RFEM 6 (Platte) | |||
| φx (L/2) [mrad] | φx (L/2) [mrad] | Ausnutzung [-] | φx (L/2) [mrad] | Ausnutzung [-] | φx (L/2) [mrad] | Ausnutzung [-] | |
| Festes Lager | 32,6 | 32,2 | 0,988 | 32,4 | 0,994 | 32,7 | 1,003 |
| Gabellagerung | 69,9 | 68,5 | 0,979 | 69,9 | 1,000 | 68,8 | 0,999 |
| Lagerung | Analytische Lösung | ANSYS 13 | RFEM 5, RF-FE-BGDK (Stab) | RFEM 5 (Platte) | |||
| φx (L/2) [mrad] | φx (L/2) [mrad] | Ausnutzung [-] | φx (L/2) [mrad] | Ausnutzung [-] | φx (L/2) [mrad] | Ausnutzung [-] | |
| Festes Lager | 32,6 | 32,2 | 0,988 | 32,6 | 1,000 | 32.5 | 0,974 |
| Gabellagerung | 69,9 | 68,5 | 0,979 | 69,9 | 1,000 | 68.1 | 0,974 |
Hinweis 1: Zur Veranschaulichung des Verwölbungseffektes soll eine Lösung mit Plattenmodellen dienen. Der relative Fehler wird auch durch die Annäherung des Gabellagers verursacht.
Hinweis 2: Numerische Lösung in ANSYS 13 wurde von der Firma Designtec sro durchgeführt Die Größen MTpri und $ MTsec sind nicht die originalen Ergebnisse aus ANSYS 13. Sie berechnen sich aus dem Wölbmoment Mω. Sie sind also nicht als völlig genaue Werte zu verstehen. Die Elemente BEAM188 werden in ANSYS 13 verwendet.