Описание работы
Консоль двутаврового профиля поддерживается на левом конце (x = 0) и нагружена крутящим моментом M согласно следующему {%ref#sketch-эскизу]]. Целью нашего примера является сравнение неподвижной опоры с вильчатой опорой и исследование поведения некоторых репрезентативных величин. Также будет выполнено сравнение с решением с помощью плит. Контрольный пример основан на примере, представленном Gensichen и Lumpe (см. ссылку). Учитываются небольшие деформации, а собственный вес не учитывается. Определите поворот в половине консоли φx (L/2), а в случае элемента стержня с депланацией определите значения первичного крутящего момента MTprim, вторичного крутящего момента M Tec и моментадепланации Mω на на левом конце (точка A) и на правом конце (точка B). Данная проблема описывается следующим набором параметров.
| Материал | Сталь | Модуль упругости | E | 210000,000 | МПа |
| Модуль сдвига | [LinkToImage06] | 81000,000 | МПа | ||
| Геометрия | консоль | Длительность | [LinkToImage03] | 5,000 | m |
| использование | Высота | h | 400,000 | мм | |
| Ширина | b | 180,000 | мм | ||
| Толщина стенки | s | 10,000 | мм | ||
| толщина полки | t | 14,000 | мм | ||
| Нагрузки | Момент | M | 1,000 | кНм | |
Аналитическое решение
При учете расчета стержня с депланацией, общий крутящий момент MT делится на первичный крутящий момент MTpri и вторичный крутящий момент MTse.
Уравнение можно представить следующим образом:
Это и есть полное дифференциальное уравнение кручения. Оно может быть решено с помощью метода начальных параметров и приводит к уравнениям для поворотаφx, относительного кручения φ'x и момента депланацииMω, первичного крутящего момента MTpri и вторичного крутящего момента MTse.
Депланация сдерживается с учетом неподвижной опоры. Граничные условия в этом случае таковы: φ(0)=0, φ'(0)=0, MT (0)=M,Mω (L)=0.
При учете вилочной опоры, включена депланация и следующие граничные условия: φ(0)=0,Mω (0)=0, MT (0)=M, Mω (L)=0.
С помощью данных граничных условий поворот φ(x) приводится к хорошо известной формуле.
Параметры RFEM
- Смоделировано в программе RFEM 5.05 и RFEM 6.01
- Размер элемента равен lFE = 0,025 м
- Используется изотропная линейная упругая модель материала
- Применяется теория изгиба пластин Кирхгофа
- Аддон Torsional Warping and Steel Design используется в RFEM 6
Результаты
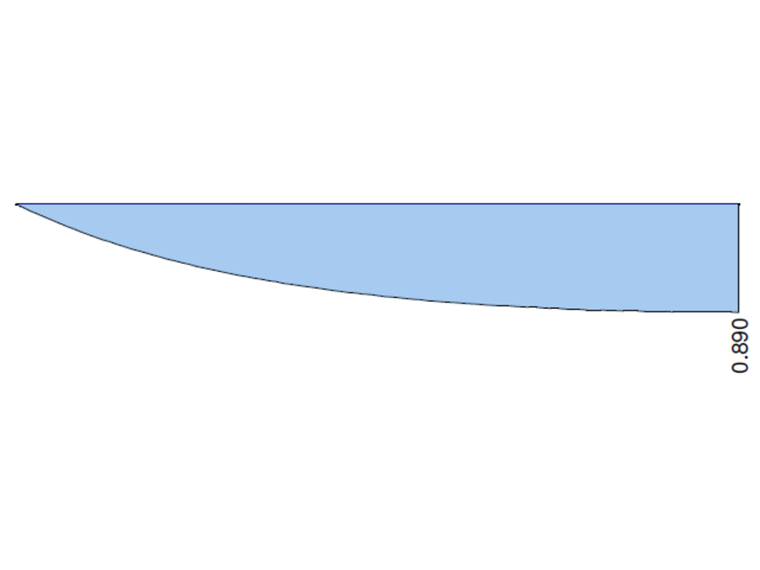
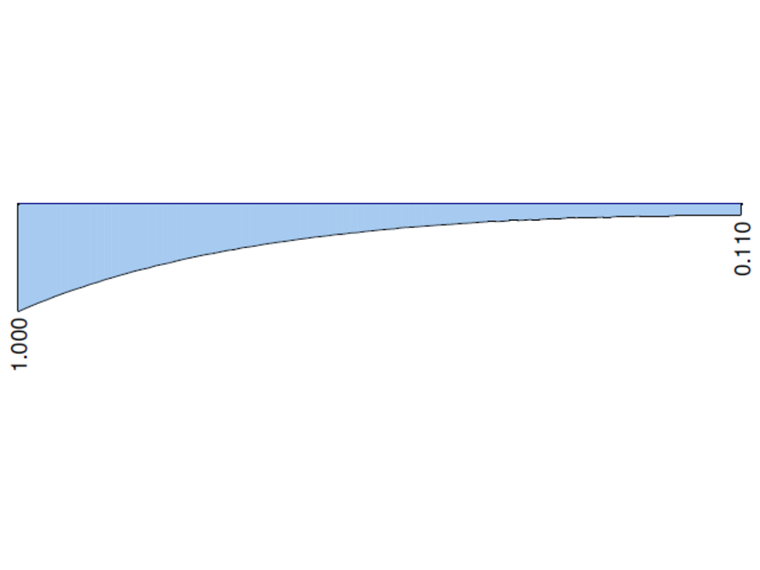
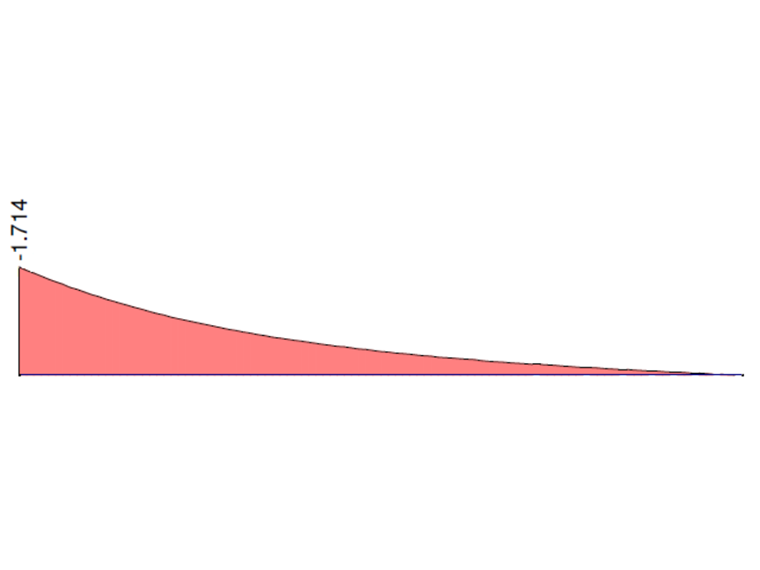
На следующих графиках показана работа общего крутящего момента MT, первичного крутящего момента MTprim, вторичного крутящего момента MTec и момента депланации Mω, рассчитанных в RFEM 6 и RFEM 5, модуль RF-FE-LTB при учете неподвижной опоры. Значения на обоих концах консоли сравниваются с аналитическим решением и решением в ANSYS 13.
| Точка A (x=0) | Аналитическое решение | ANSYS 13 (английская версия) | сечения | Rfem 6 | сечения | RFEM-FE-LTB (английская версия) | сечения |
| MTpri [кНм] | 0,000 | 0,008 | - | 0,000 | - | 0,000 | - |
| MTse [кНм] | 1,000 | 0,992 | 0,992 | 1,000 | 1,000 | 1,000 | 1,000 |
| Mω [кНм] | -1,714 | -1,683 | 0,989 | -1,743 | 1,017 | -1,714 | 1,000 |
| Точка B (x=L) | Аналитическое решение | ANSYS 13 (английская версия) | сечения | Rfem 6 | сечения | RFEM-FE-LTB (английская версия) | сечения |
| MTpri [кНм] | 0,890 | 0,893 | 1,003 | 0,869 | 0,976 | 0,890 | 1,000 |
| MTse [кНм] | 0,110 | 0,107 | 0,973 | 0,131 | 1,191 | 0,110 | 1,000 |
| Mω [кНм] | 0,000 | 0,001 | - | 0,000 | - | 0,000 | - |
Вычисленный поворот вокруг оси x можно сравнить с результатами, когда в расчете находится вильчатая опора, а также с результатами моделей пластин, которые естественно учитывают депланацию. Поворот на половине длины φ(L/2) у пластинчатых моделей применяется из-за зоны воздействия вблизи точки нагрузки. В случае пластинчатой модели задание вилочной опоры более сложное, потому что момент депланации должен быть равен нулю. Однако, данное граничное условие нельзя задать напрямую в RFEM 5/RFEM 6. Использованное приближение показано на следующем рисунке. Поворот вокруг оси x сдерживается на всех краях опоры. Только центральный узел (на оси) полностью закреплен. В случае неподвижной опоры, закреплены все края опоры.
| Поддержка | Аналитическое решение | ANSYS 13 (английская версия) | RFEM 6 (стержень) | RFEM 6 (пластина) | |||
| φx (L/2) [мрад] | φx (L/2) [мрад] | Соотношение [-] | φx (L/2) [мрад] | Соотношение [-] | φx (L/2) [мрад] | Соотношение [-] | |
| Неподвижная опора | 32,6 | 32,2 | 0,988 | 32,4 | 0,994 | 32,7 | 1,003 |
| Вилочная опора | 69,9 | 68,5 | 0,979 | 69,9 | 1,000 | 68,8 | 0,999 |
| Поддержка | Аналитическое решение | ANSYS 13 (английская версия) | RFEM 5, RF-FE-LTB (стержень) | RFEM 5 (плита) | |||
| φx (L/2) [мрад] | φx (L/2) [мрад] | Соотношение [-] | φx (L/2) [мрад] | Соотношение [-] | φx (L/2) [мрад] | Соотношение [-] | |
| Неподвижная опора | 32,6 | 32,2 | 0,988 | 32,6 | 1,000 | 32,5 | 0,974 |
| Вилочная опора | 69,9 | 68,5 | 0,979 | 69,9 | 1,000 | 68.1 | 0,974 |
Замечание 1: Решение с моделями пластин будет использовано для демонстрации эффекта депланации. Относительная погрешность вызвана также приближением вилочной опоры.
Замечание 2: Численное решение в ANSYS 13 было выполнено компанией Designtec sro. Величины MTprim и $ MTec не являются первоначальными результатами из ANSYS 13. Они рассчитываются по моменту депланации Mω. Поэтому их не следует воспринимать как абсолютно точные значения. Элементы BEAM188 используются в ANSYS 13.