Descrizione
Uno sbalzo del profilo a I è supportato sull'estremità sinistra (x=0) ed è caricato dalla coppia M secondo il seguente . Lo scopo di questo esempio è confrontare il vincolo fisso con il vincolo esterno a forcella e studiare il comportamento di alcune grandezze rappresentative. Viene anche eseguito il confronto con la soluzione tramite piastre. L'esempio di verifica si basa sull'esempio introdotto da Gensichen e Lumpe (vedere il riferimento). Vengono considerate piccole deformazioni e il peso proprio è trascurato. Determinare la rotazione nella metà dello sbalzo φx (L/2) e, nel caso dell'entità dell'asta con ingobbamento, determinare i valori del momento torcente primario MTpri, del momento torcente secondario MTsec e del momento di ingobbamento Mω entrambi su all'estremità sinistra (punto A) e all'estremità destra (punto B). Il problema è descritto dal seguente set di parametri.
| Materiale | Acciaio | Modulo di elasticità | E | 210000,000 | MPa |
| Modulo di taglio | [LinkToImage01] | 81000,000 | MPa | ||
| Geometria | Sbalzo | Durata | [LinkToImage01] | 5,000 | m |
| Sezione trasversale | Altezza | h | 400,000 | mm | |
| Larghezza | b | 180,000 | mm | ||
| Spessore dell'anima | s | 10,000 | mm | ||
| spessore dell'ala | t | 14,000 | mm | ||
| Carico | Momento | M | 1,000 | kNm | |
Soluzione analitica
Quando si considera il calcolo dell'asta con ingobbamento, il momento torcente totale MT è diviso tra il momento torcente primario MTpri e il momento torcente secondario MTsec.
L'equazione può essere espressa come segue:
Questa è l'equazione differenziale completa della torsione. Può essere risolto con il metodo dei parametri iniziali e risulta nelle equazioni per la rotazione φx, la torsione relativa φ'x e il momento di ingobbamento Mω, il momento torcente primario MTpri e il momento torcente secondario MTsec.
L'ingobbamento è vincolato, quando si considera il vincolo esterno fisso. Le condizioni al contorno in questo caso sono: φ(0)=0, φ'(0)=0, MT (0)=M, Mω (L)=0.
Quando si considera il vincolo esterno della forcella, l'ingobbamento è abilitato e le condizioni al contorno sono le seguenti: φ(0)=0,Mω (0)=0, MT (0)=M, Mω (L)=0.
Utilizzando queste condizioni al contorno, la rotazione φ(x) risulta nella formula ben nota.
Impostazioni di RFEM
- Modellato in RFEM 5.05 e RFEM 6.01
- La dimensione dell'elemento è lFE = 0,025 m
- Viene utilizzato il modello di materiale elastico lineare isotropo
- Viene utilizzata la teoria della flessione della piastra di Kirchhoff
- L'add-on Torsione di ingobbamento e verifica acciaio è utilizzato in RFEM 6
Risultati
Nei grafici seguenti sono mostrati i comportamenti del momento torcente totale MT, del momento torcente primario MTpri, del momento torcente secondario MTsec e del momento di ingobbamento Mω calcolato in RFEM 6 e RFEM 5, modulo RF-FE-LTB, quando si considera il vincolo esterno fisso. I valori su entrambe le estremità dello sbalzo sono confrontati con la soluzione analitica e la soluzione in ANSYS 13.
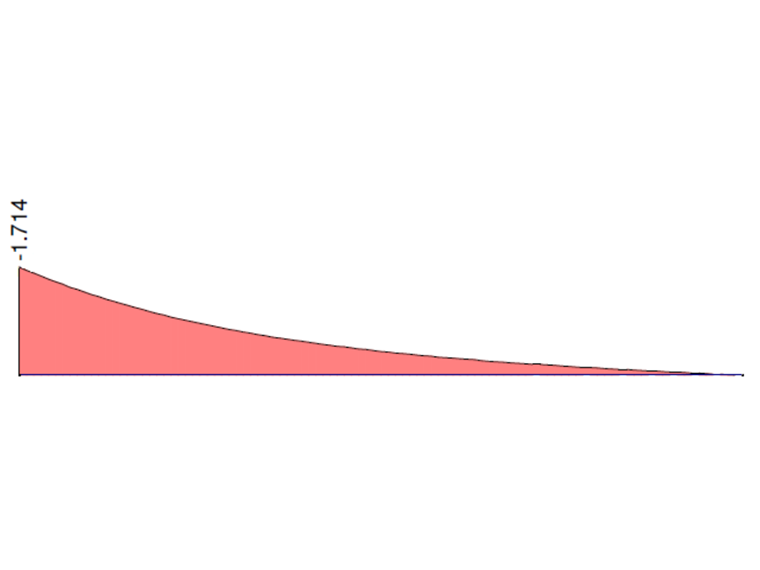
| Punto A (x=0) | Soluzione analitica | ANSYS 13 | Rapporto | RFEM 6 | Rapporto | RFEM RF-FE-LTB | Rapporto |
| MTpri [kNm] | 0,000 | 0,008 | - | 0,000 | - | 0,000 | - |
| MTsec [kNm] | 1,000 | 0,992 | 0,992 | 1,000 | 1,000 | 1,000 | 1,000 |
| Mω [kNm] | -1.714 | -1.683 | 0,989 | -1.743 | 1,017 | -1.714 | 1,000 |
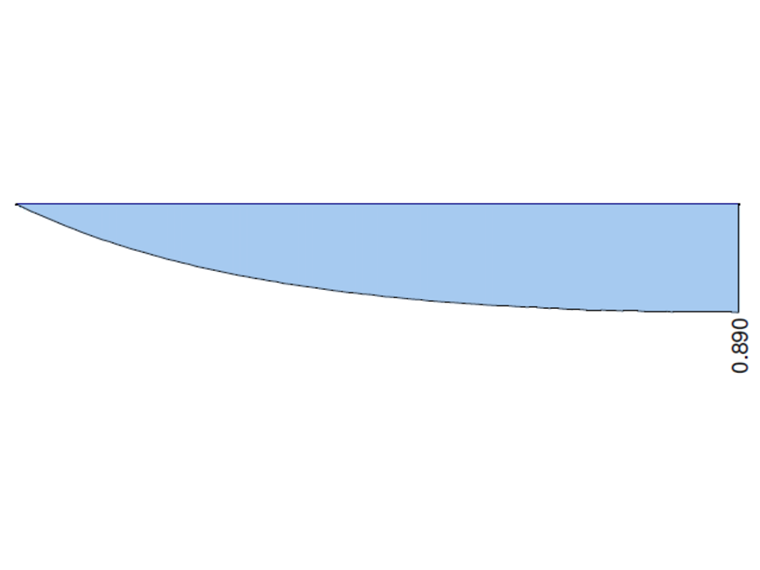
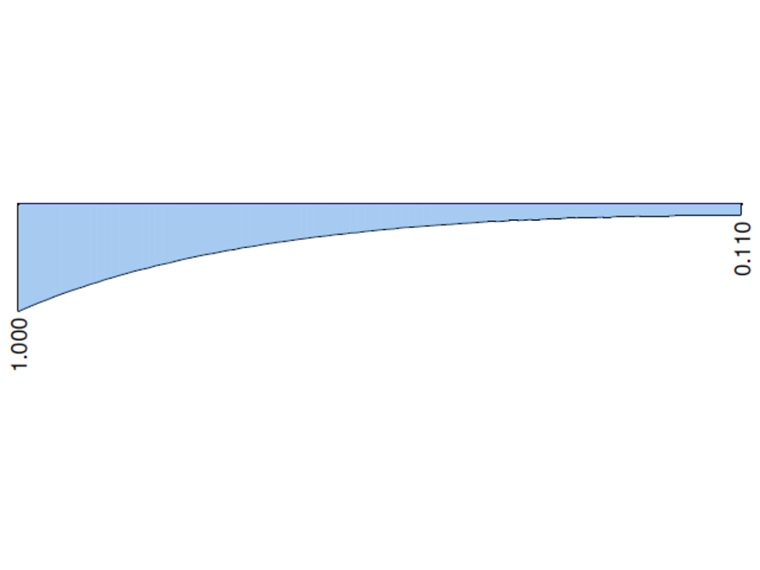
| Punto B (x=L) | Soluzione analitica | ANSYS 13 | Rapporto | RFEM 6 | Rapporto | RFEM RF-FE-LTB | Rapporto |
| MTpri [kNm] | 0,890 | 0,893 | 1,003 | 0,869 | 0,976 | 0,890 | 1,000 |
| MTsec [kNm] | 0,110 | 0,107 | 0,973 | 0,131 | 1,191 | 0,110 | 1,000 |
| Mω [kNm] | 0,000 | 0,001 | - | 0,000 | - | 0,000 | - |
La rotazione calcolata attorno all'asse x può essere confrontata con i risultati, quando si considera il vincolo esterno della forcella e anche con i modelli delle piastre, che tengono conto dell'ingobbamento naturale. La rotazione a metà lunghezza φ(L/2) viene utilizzata a causa dell'area interessata nelle vicinanze del punto di carico nel caso di modelli con piastra. La definizione del vincolo esterno della forcella nel caso del modello a piastra è complicata, perché il momento di ingobbamento deve essere uguale a zero. Questa condizione al contorno non può essere impostata direttamente in RFEM 5/RFEM 6. L'approssimazione utilizzata è mostrata nella seguente figura. La rotazione intorno all'asse x è vincolata su tutti i bordi del vincolo esterno. Solo il nodo centrale (sull'asse) è completamente fissato. In caso di vincolo fisso, tutti i bordi del vincolo esterno sono fissi.
| Supporto | Soluzione analitica | ANSYS 13 | RFEM 6 (asta) | RFEM 6 (piastra) | |||
| φx (L/2) [mrad] | φx (L/2) [mrad] | Rapporto [-] | φx (L/2) [mrad] | Rapporto [-] | φx (L/2) [mrad] | Rapporto [-] | |
| Vincolo a incastro | 32,6 | 32,2 | 0,988 | 32,4 | 0,994 | 32,7 | 1,003 |
| Supporto a forcella | 69,9 | 68.5 | 0,979 | 69.9 | 1,000 | 68,8 | 0,999 |
| Supporto | Soluzione analitica | ANSYS 13 | RFEM 5, RF-FE-LTB (asta) | RFEM 5 (piastra) | |||
| φx (L/2) [mrad] | φx (L/2) [mrad] | Rapporto [-] | φx (L/2) [mrad] | Rapporto [-] | φx (L/2) [mrad] | Rapporto [-] | |
| Vincolo a incastro | 32,6 | 32,2 | 0,988 | 32,6 | 1,000 | 32,5 | 0,974 |
| Supporto a forcella | 69,9 | 68.5 | 0,979 | 69,9 | 1,000 | 68,1 | 0,974 |
Osservazione 1: La soluzione con i modelli a piastra viene utilizzata come dimostrazione dell'effetto di ingobbamento. L'errore relativo è causato anche dall'approssimazione del vincolo esterno della forcella.
Osservazione 2: La soluzione numerica in ANSYS 13 è stata eseguita dalla società Designtec sro Le quantità MTpri e $ MTsec non sono i risultati originali di ANSYS 13. Sono calcolati dal momento di ingobbamento Mω. Quindi non dovrebbero essere presi come valori del tutto accurati. Gli elementi BEAM188 sono utilizzati in ANSYS 13.