Descripción del trabajo
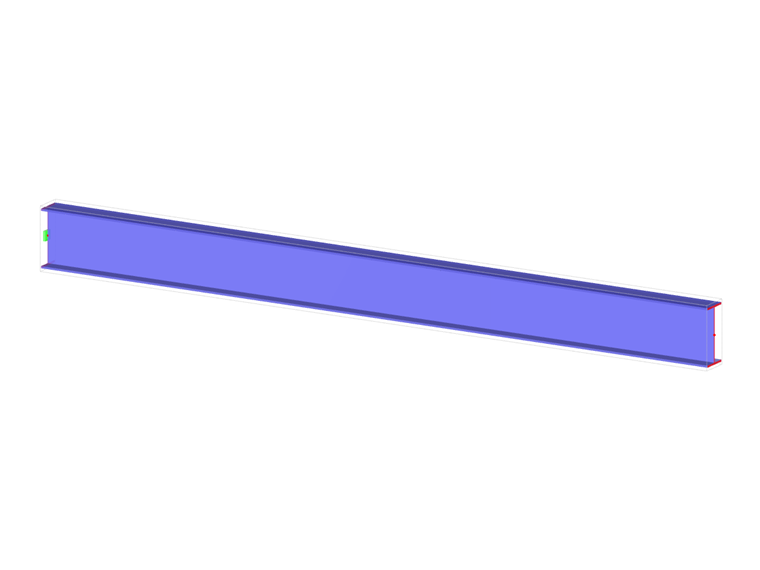
Un voladizo de perfil en I está apoyado en el extremo izquierdo (x=0) y está cargado con el par M según el siguiente sketch. El objetivo de este ejemplo es comparar el apoyo fijo con el apoyo en horquilla e investigar el comportamiento de algunas cantidades representativas. También se realiza la comparación con la solución por medio de placas. El ejemplo de verificación se basa en el ejemplo presentado por Gensichen y Lumpe (ver la referencia). Se consideran las deformaciones pequeñas y se omite el peso propio. Determine el giro en la mitad del voladizo φx (L/2) y en el caso de la entidad de barra con alabeo determine los valores del momento torsor primario MTpri, el momento torsor secundario MTsec y el momento de alabeo Mω ambos en el extremo izquierdo (punto A) y en el extremo derecho (punto B). El problema se describe mediante el siguiente conjunto de parámetros.
| Material | Acero | Módulo de elasticidad | E | 210000,000 | MPa |
| Módulo de cortante | [LinkToImage06] | 81000,000 | MPa | ||
| Geometría | Voladizo | perímetro | L | 5,000 | m |
| Sección | Altitud | h | 400,000 | mm | |
| Ancho | b | 180,000 | mm | ||
| Espesor de alma | s | 10,000 | mm | ||
| espesor del ala | t | 14,000 | mm | ||
| Carga | Momento | M | 1,000 | kNm | |
Solución analítica
Cuando se considera el cálculo de barras con alabeo, el momento torsor total MT se divide entre el momento torsor principal MTpri y el momento torsor secundario MTsec.
La ecuación se puede expresar de la siguiente manera:
Esta es la ecuación diferencial completa de la torsión. Se puede resolver mediante el método de los parámetros iniciales y da como resultado ecuaciones para el giro φx, la torsión relativa φ'x y el momento de alabeo Mω, el momento torsor primario MTpri y el momento torsor secundario MTsec.
El alabeo está coaccionado cuando se considera el apoyo fijo. Las condiciones de contorno en este caso son: φ(0)=0, φ'(0)=0, MT (0)=M, Mω (L)=0.
Cuando se considera el apoyo en horquilla, se habilita el alabeo y las condiciones de contorno son las siguientes: φ(0)=0,Mω (0)=0, MT (0)=M,Mω (L)=0.
Usando esas condiciones de contorno, el giro φ(x) da como resultado la fórmula conocida.
Configuración de RFEM
- Modelado en RFEM 5.05 y RFEM 6.01
- El tamaño del elemento es lFE = 0,025 m
- Se utiliza el modelo de material elástico lineal isótropo
- Se utiliza la teoría de flexión de la placa de Kirchhoff
- El complemento Alabeo por torsión y Cálculo de acero se utiliza en RFEM 6
Resultados
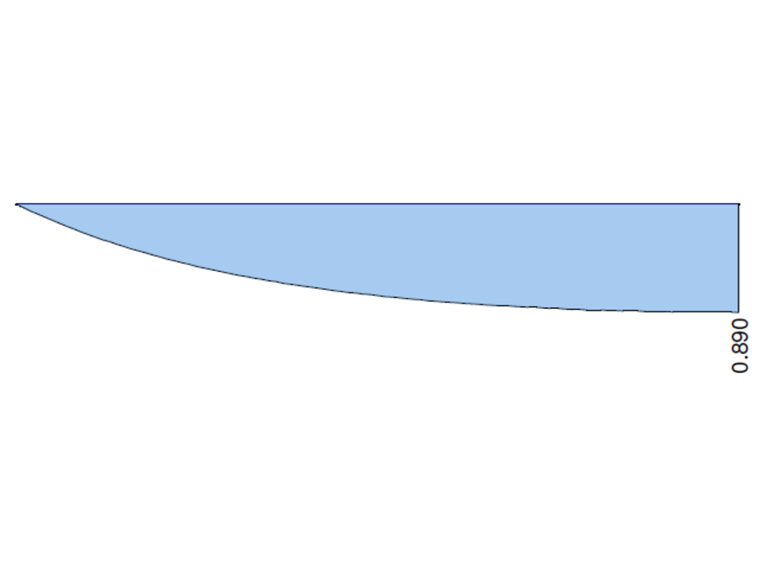
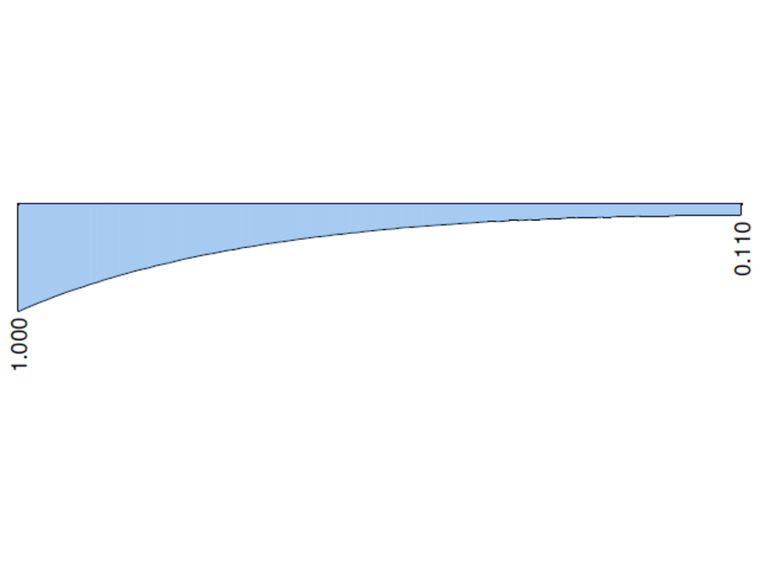
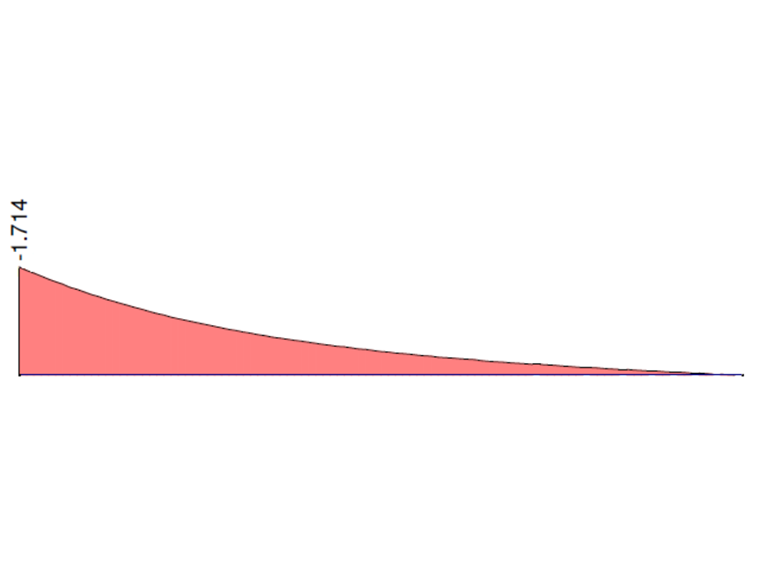
En los siguientes gráficos se muestran los comportamientos del momento torsor total MT, el momento torsor primario MTpri, el momento torsor secundario MTsec y el momento de alabeo Mω calculado en RFEM 6 y RFEM 5, módulo RF-FE-LTB, cuando se considera el apoyo fijo. Los valores en ambos extremos del voladizo se comparan con la solución analítica y la solución en ANSYS 13.
| Punto A (x=0) | Solución analítica | ANSYS 13 | Razón | RFEM 6 | Razón | RFEM RF-FE-LTB | Razón |
| MTpri [kNm] | 0,000 | 0,008 | |||||
| 0,000 | |||||||
| 0,000 | |||||||
| MTsec [kNm] | 1,000 | 0,992 | 0,992 | 1,000 | 1,000 | 1,000 | 1,000 |
| Mω [kNm] | -1,714 | -1,683 | 0,989 | -1,743 | 1,017 | -1,714 | 1,000 |
| Punto B (x=L) | Solución analítica | ANSYS 13 | Razón | RFEM 6 | Razón | RFEM RF-FE-LTB | Razón |
| MTpri [kNm] | 0,890 | 0,893 | 1,003 | 0,869 | 0,976 | 0,890 | 1,000 |
| MTsec [kNm] | 0,110 | 0,107 | 0,973 | 0,131 | 1,191 | 0,110 | 1,000 |
| Mω [kNm] | 0,000 | 0,001 | |||||
| 0,000 | |||||||
| 0,000 |
El giro calculado alrededor del eje x se puede comparar con los resultados cuando se considera el apoyo en horquilla y también con los modelos de placas, que tienen en cuenta el alabeo de forma natural. El giro en la longitud media φ(L/2) se usa debido al área afectada en las inmediaciones del punto de carga en el caso de modelos de placas. La definición del apoyo en horquilla en el caso del modelo de placa es complicada, porque el momento de alabeo tiene que ser igual a cero. Esta condición de contorno no se puede establecer directamente en RFEM 5/RFEM 6. La aproximación utilizada se muestra en la siguiente figura. El giro alrededor del eje x está restringido en todos los bordes del apoyo. Solo el nudo central (en el eje) está completamente fijo. En el caso de un apoyo fijo, todos los bordes del apoyo son fijos.
| Apoyo | Solución analítica | ANSYS 13 | RFEM 6 (barra) | RFEM 6 (placa) | |||
| φx (L/2) [mrad] | φx (L/2) [mrad] | Razón [-] | φx (L/2) [mrad] | Razón [-] | φx (L/2) [mrad] | Razón [-] | |
| empotrado | 32,6 | 32,2 | 0,988 | 32,4 | 0,994 | 32,7 | 1,003 |
| Apoyo en horquilla | 69,9 | 68,5 | 0,979 | 69,9 | 1,000 | 68,8 | 0,999 |
| Apoyo | Solución analítica | ANSYS 13 | RFEM 5, RF-FE-LTB (barra) | RFEM 5 (placa) | |||
| φx (L/2) [mrad] | φx (L/2) [mrad] | Razón [-] | φx (L/2) [mrad] | Razón [-] | φx (L/2) [mrad] | Razón [-] | |
| empotrado | 32,6 | 32,2 | 0,988 | 32,6 | 1,000 | 32.5 | 0,974 |
| Apoyo en horquilla | 69,9 | 68,5 | 0,979 | 69,9 | 1,000 | 68.1 | 0,974 |
Observación 1: La solución con modelos de placas se utiliza como demostración del efecto de alabeo. El error relativo también se debe a la aproximación del apoyo en horquilla.
Observación 2: La solución numérica en ANSYS 13 fue realizada por la empresa Designtec sro Las cantidades MTpri y $ MTsec no son los resultados originales de ANSYS 13. Se calculan a partir del momento de alabeoMω. Por lo tanto, no se deben tomar como valores completamente precisos. Los elementos BEAM188 se utilizan en ANSYS 13.