Descrição
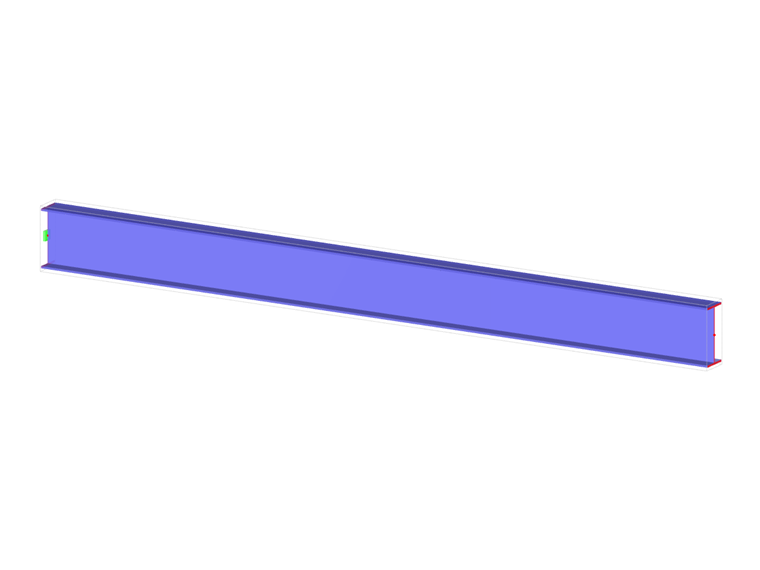
A viga em consola com um perfil em I é suportada na extremidade esquerda (x=0) e é carregada por um momento torcional M de acordo com o seguinte . O objetivo deste exemplo é comparar o apoio fixo com o apoio em forquilha e analisar o comportamento de alguns valores representativos. A comparação com a solução através de lajes também é realizada. O exemplo de verificação é baseado no exemplo introduzido por Gensichen e Lumpe (ver referência). São consideradas pequenas deformações e o peso próprio é negligenciado. Determinar a rotação na metade da consola φx (L/2) e no caso da entidade de barra com empenamento determinar os valores do momento de torção primário MTpri, o momento de torção secundário MTsec e o momento de empenamento Mω, ambos em extremidade esquerda (ponto A) e na extremidade direita (ponto B). O problema é descrito pelo seguinte conjunto de parâmetros.
| Material | Aço de armadura | Módulo de elasticidade | E | 210000,000 | MPa |
| Módulo de corte | G | 81000,000 | MPa | ||
| Geometria | Viga em consola | perímetro | [LinkToImage04] | 5,000 | m |
| Secção | Altura | h | 400,000 | mm | |
| Largura | B | 180,000 | mm | ||
| Espessura de alma | S | 10,000 | mm | ||
| Espessura de banzo | t | 14,000 | mm | ||
| Carga, | Momento | M | 1,000 | kNm | |
Solução analítica
Quando considera o cálculo de barra com empenamento o momento de torção totalMT é dividido entre o momento de torção primário M Tprie o momento de torção secundário MTsec.
A equação pode ser expressa da seguinte forma:
Esta é a equação diferencial completa da torção. Pode ser resolvido pelo método dos parâmetros iniciais e resultados em equações para a rotação φx, torção relativa φ'x e momento de empenamento Mω, momento de torção primário MTpri e momento de torção secundário MTsec.
O empenamento é contido quando é considerado o apoio fixo. As condições de fronteira neste caso são: φ (0) = 0, φ ' (0) = 0, MT (0) = M, Mω (L) = 0.
Quando é considerado o apoio de forquilha, o empenamento é possibilitado e as condições de fronteira são as seguintes: φ(0)=0,Mω (0)=0, MT (0)=M, Mω (L)=0.
Utilizando estas condições de fronteira, a rotação φ(x) resulta numa fórmula bem conhecida.
Configuração do RFEM
- Modelado no RFEM 5.05 e no RFEM 6.01
- O tamanho do elemento é lFE = 0,025 m
- É utilizado um modelo de material isotrópico linear elástico
- Foi utilizada a teoria de flexão de placas de Kirchhoff
- Módulo Torção com empenamento e dimensionamento de aço utilizado no RFEM 6
Resultados
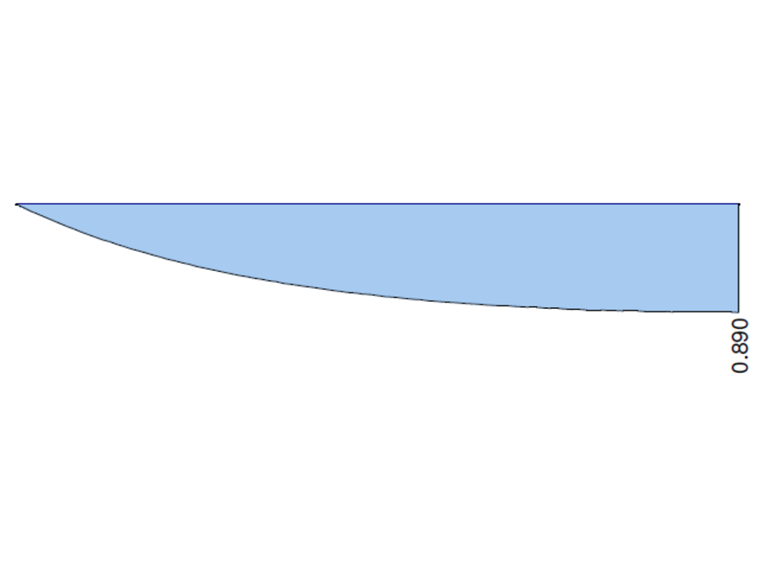
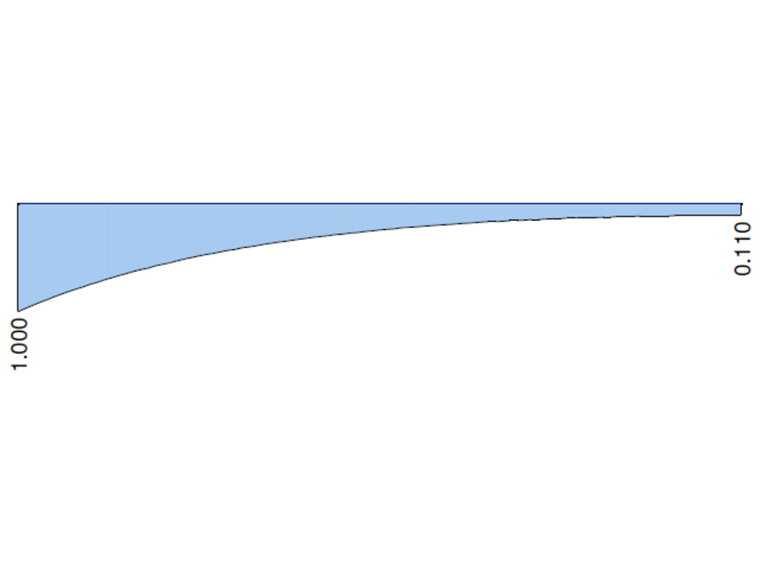
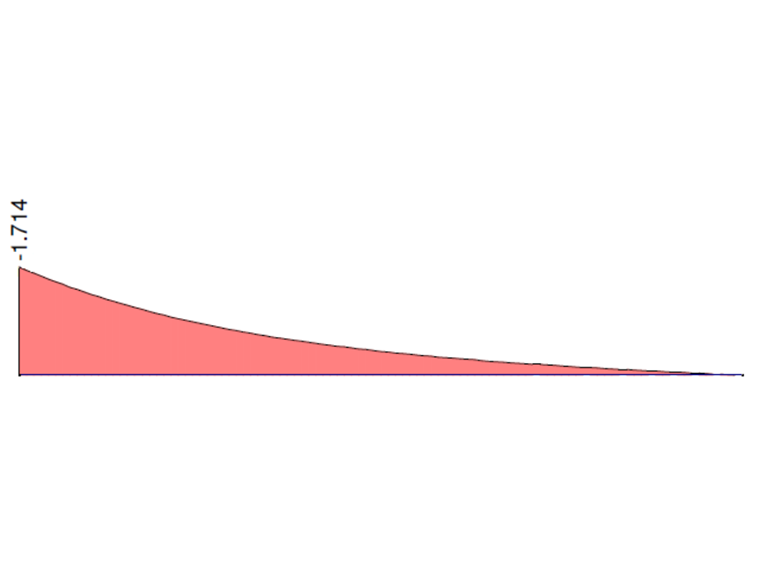
Nos gráficos seguintes são apresentados os comportamentos do momento de torção total MT, o momento de torção primário MTpri, o momento de torção secundário MTsec e o momento de empenamento Mω calculados no RFEM 6 e RFEM 5, módulo RF-FE-LTB, quando é considerado o apoio fixo. Os valores nas duas extremidades da consola são comparados com a solução analítica e a solução no ANSYS 13.
| Ponto A (x=0) | Solução analítica | ANSYS 13 | Relação | RFEM 6 | Relação | RFEM RF-FE-LTB (em inglês) | Relação |
| MTpri [kNm] | 0,000 | 0,008 | - | 0,000 | - | 0,000 | - |
| MTsec [kNm] | 1,000 | 0,992 | 0,992 | 1,000 | 1,000 | 1,000 | 1,000 |
| Mω [kNm] | -1.714 | -1683 | 0,989 | -1.743 | 1,017 | -1.714 | 1,000 |
| Ponto B (x=L) | Solução analítica | ANSYS 13 | Relação | RFEM 6 | Relação | RFEM RF-FE-LTB (em inglês) | Relação |
| MTpri [kNm] | 0,890 | 0,893 | 1,003 | 0,869 | 0,976 | 0,890 | 1,000 |
| MTsec [kNm] | 0,110 | 0,107 | 0,973 | 0,131 | 1,191 | 0,110 | 1,000 |
| Mω [kNm] | 0,000 | 0,001 | - | 0,000 | - | 0,000 | - |
A rotação calculada em torno do eixo x pode ser comparada com os resultados quando o apoio do forquilha é considerado e também com os modelos de placa, que têm em consideração o empenamento naturalmente. A rotação a meio do comprimento φ(L/2) é utilizada devido à área afetada na proximidade do ponto de carregamento no caso de modelos de placas. A definição do apoio de forquilha no caso do modelo da placa é complicada porque o momento de empenamento tem de ser igual a zero. Esta condição de fronteira não pode ser definida diretamente no RFEM 5/RFEM 6. A aproximação utilizada é apresentada na seguinte #fig. A rotação em torno do eixo x é restringida em todas as bordas do apoio. Apenas o nó central (no eixo) está completamente fixo. No caso de um apoio fixo, todas as bordas do apoio estão fixas.
| Apoio | Solução analítica | ANSYS 13 | RFEM 6 (barra) | RFEM 6 (placa) | |||
| φx (L/2) [mrad] | φx (L/2) [mrad] | Relação [-] | φx (L/2) [mrad] | Relação [-] | φx (L/2) [mrad] | Relação [-] | |
| restrição | 32,6 | 32,2 | 0,988 | 32,4 | 0,994 | 32,7 | 1,003 |
| Apoio de forquilha | 69,9 | 68,5 | 0,979 | 69,9 | 1,000 | 68,8 | 0,999 |
| Apoio | Solução analítica | ANSYS 13 | RFEM 5, RF-FE-LTB (barra) | RFEM 5 (placa) | |||
| φx (L/2) [mrad] | φx (L/2) [mrad] | Relação [-] | φx (L/2) [mrad] | Relação [-] | φx (L/2) [mrad] | Relação [-] | |
| restrição | 32,6 | 32,2 | 0,988 | 32,6 | 1,000 | 32.5 | 0,974 |
| Apoio de forquilha | 69,9 | 68,5 | 0,979 | 69,9 | 1,000 | 68.1 | 0,974 |
Nota 1: A solução com modelos de placas é utilizada para demonstrar o efeito de empenamento. O erro relativo é causado também pela aproximação do apoio da forquilha.
Nota 2: A solução numérica em ANSYS 13 foi realizada pela empresa Designtec sro As quantidades MTpri e $ MTsec não são os resultados originais do ANSYS 13. Estas são calculadas a partir do momento de empenamento Mω. Assim, não devem ser considerados como valores totalmente precisos. Os elementos BEAM188 são utilizados no ANSYS 13.