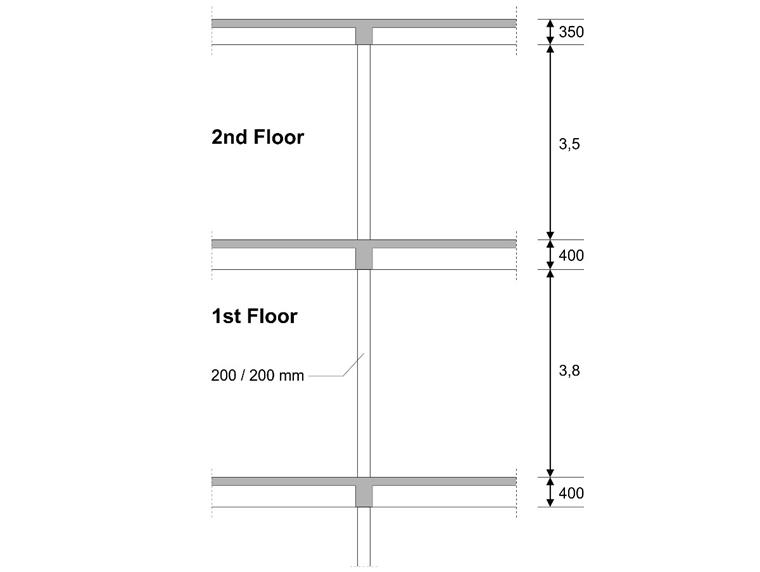
Se diseña una columna interna en el primer piso de un edificio de tres pisos. La columna es monolítica y está conectada a las vigas superior e inferior. Luego, se verifica el método simplificado de diseño contra incendios A para columnas según DIN EN 1992-1-2 y se comparan los resultados con [1]].
| Material | Hormigón C35/45 | Valor de diseño de la resistencia a compresión del hormigón | fcd | 19.900 | N/mm2 |
| Acero de refuerzo B500S(B) | Resistencia de fluencia de diseño | fyd | 434.783 | N/mm2 | |
| Geometría | Estructura | Longitud de la columna | lcolumn | 4.200 | m |
| Sección transversal | Altura | h | 200 | mm | |
| Ancho | b | 200 | mm | ||
| Área de la sección transversal | Ac | 400 | mm2 | ||
| Cargas | Cargas Permanentes | LC1 | Gk | 363.000 | kN |
| LC2 | Sk | 30.000 | kN | ||
| LC3 | Qk | 150.000 | kN |
Configuraciones de RFEM
- El método simplificado según el Capítulo 5 está activado como el método para diseño contra incendios.
- Permanente y transitorio para temperatura normal según 2.4.2(2) es el tipo de situación de diseño para cargas de incendio.
- El factor de reducción del nivel de carga de diseño ηfi se establece en 0.61.
- El pandeo lateral ky para el diseño de incendio se establece en 0.5.
Resultados
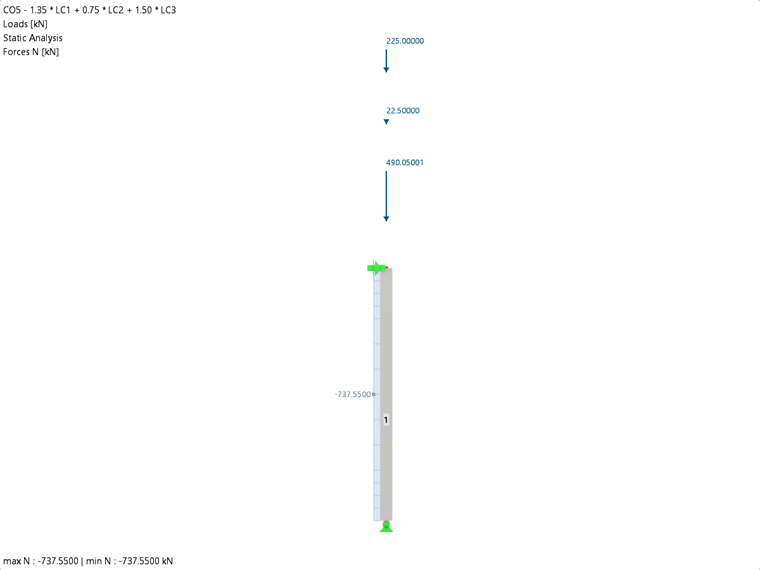
- Fuerzas internas
La combinación de carga dominante: 1.35·LC1 + 0.75·LC2 + 1.5·LC3
Fuerza normal NEd [kN] RFEM Solución analítica Proporción 737.550 738.000 1.00
- Longitud efectiva y esbeltez
'Longitud efectiva y esbeltez Parámetro Descripción Unidad RFEM Solución analítica Proporción ky Factor de longitud efectiva – 1.000 1.000 1.00 l0 Longitud efectiva m 4.200 4.200 1.00 l0 Longitud efectiva m 4.200 4.200 1.00 n Fuerza normal relativa – 0.930 0.932 1.00 iy Radio de giro – 57.700 57.700 1.00 λ Esbeltez – 72.746 73.000 0.99
- Refuerzo requerido
Parámetro Descripción Unidad RFEM Solución analítica Proporción As,min Área mínima de refuerzo longitudinal cm2 2.540 2.540 1.00 As,req refuerzo requerido cm2 12.480 12.400 1.00
- Diseño contra incendios
Se considera que el edificio donde se encuentra la columna es de clase de edificio 4. Por lo tanto, el requisito para la columna es una duración de resistencia al fuego de al menos R60. Primero, se calcula la dimensión mínima de la sección según el método simplificado A para columnas según 5.3.2(1), Tabla 5.2(a):
Dimensión mínima de la sección y distancia del eje de refuerzo según 5.3.2(1) Tabla 5.2a Parámetro Descripción Unidad RFEM Solución analítica Proporción ηfi Factor de reducción del nivel de carga de diseño para situación de incendio – 0.610 0.614 1.00 NEd,fi Fuerza axial en la sección debido a la carga para diseño de incendio kN 452.856 453.000 1.00 NRd Capacidad de la columna kN 798.835 800.000 1.00 μfi Grado de utilización en situación de incendio kN 0.570 0.566 1.00 bmin,req Dimensión mínima requerida de la sección transversal mm 216.7 217.0 1.00 am,req Distancia mínima requerida mm 39.3 39.3 1.00
Además, se determina la duración mínima del incendio R. Se calcula de la siguiente manera:
Se utiliza la siguiente ecuación para calcular la resistencia al fuego determinada sobre la base de la capacidad de resistencia Rη,fi:
Para propósitos de simplificación, la literatura asume que μfi = ηfi. Por lo tanto, es necesario recalcular Rη,fi utilizando el grado real de utilización en una situación de incendio μfi para poder compararlo con los resultados de RFEM:
| Duración mínima del incendio según Eq. 5.7 | |||||
| Parámetro | Descripción | Unidad | RFEM | Solución analítica | Proporción |
| μfi | Grado de utilización en una situación de incendio | kN | 0.570 | 0.570 | 1.00 |
| ω | Proporción de reforzamiento mecánico | – | 0.689 | 0.690 | 1.00 |
| Rη,fi | Resistencia al fuego determinada sobre la base de la capacidad de resistencia | – | 35.948 | 35.690 | 1.00 |
| Ra | Resistencia al fuego determinada sobre la base de la cobertura del refuerzo | – | 16.000 | 16.000 | 1.00 |
| Ri | Resistencia al fuego determinada sobre la base de la longitud de pandeo | – | 27.840 | 27.800 | 1.00 |
| Rb | Resistencia al fuego determinada sobre la base de la dimensión de la sección transversal | – | 18.000 | 18.000 | 1.00 |
| Rn | Resistencia al fuego determinada sobre la base del número de barras | – | 0 | 0 | 1.00 |
| R | Tiempo de resistencia al fuego | min | 83 | 82 | 1.01 |