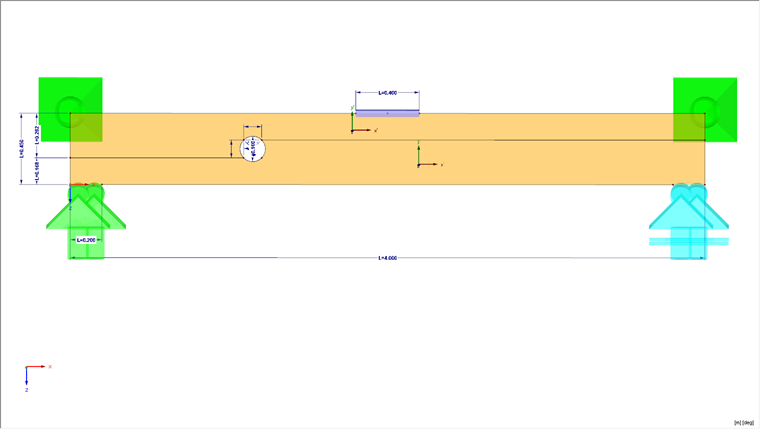
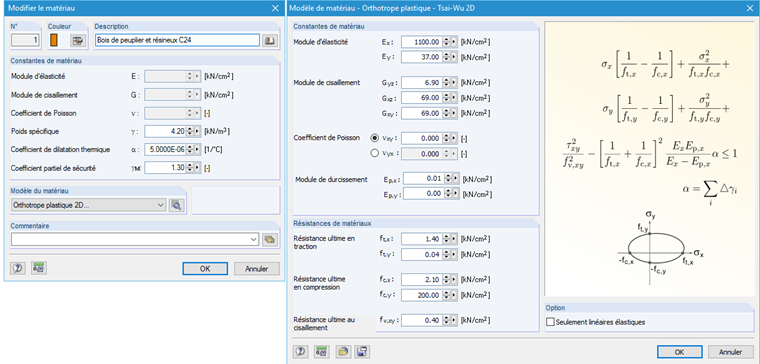
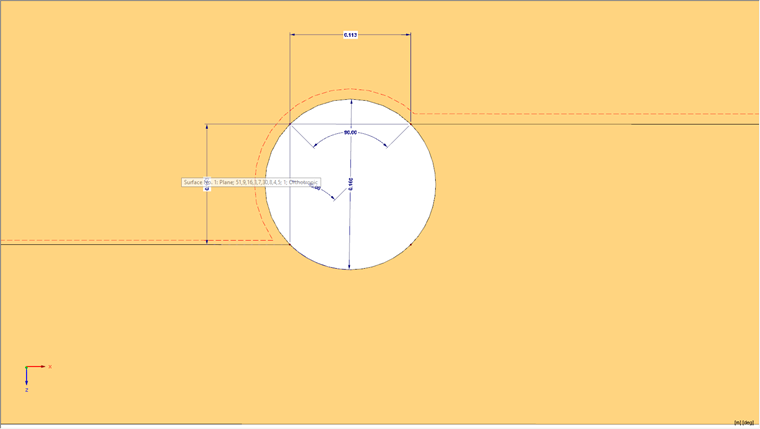
La poutre doit avoir une cotation de 4000 mm, une hauteur de 450 mm et une largeur de 120 mm. La simulation doit être effectuée avec un diamètre de trou de 0,4 ∙ profondeur de poutre. Le bois C24 est utilisé comme matériau et le modèle de matériau plastique orthotrope est utilisé comme modèle de matériau, cela représente le bois composite. La simulation des fissures est modélisée à l’aide d’une libération linéique.
La fissure attendue dans le modèle se produit avec un décalage de 45° par rapport au centre du cercle au bord de l’ouverture. La fissure s’est formée le long de la fibre et peut ainsi être considérée comme une rupture de cisaillement roulant. La libération linéique agit comme un élément d’interface dans lequel une double ligne est simulée, couplée via les propriétés de contact. Pour les propriétés de contact, les propriétés de matériau selon la clause 4.4 de [1] sont utilisées dans dans le modèle. Les propriétés de matériau sont calculées à l’avance sous forme de diagrammes pour la libération linéique, puis assignées à la libération linéique.
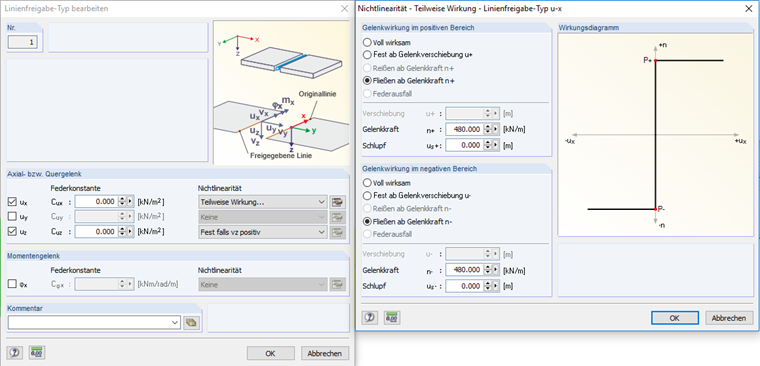
Définition d’une libération linéique
Pour attribuer les propriétés de matériau à la libération linéique, le logiciel crée des propriétés d’assemblage non-linéaires. Un diagramme est utilisé à cet effet dans notre exemple. Afin de considérer correctement le cisaillement roulant, un diagramme est créé pour la rupture de cisaillement (le long de l’axe local x de la ligne) et un diagramme pour la rupture de traction transversale (axe local z de la ligne). Dans ce cas, la rupture de cisaillement peut être répartie dans les directions X positive et négative, tandis que la rupture de traction transversale est décrite dans le diagramme par les valeurs du quatrième quadrant (c’est-à-dire la rupture de traction). Une valeur de 0,04 kN/cm² est utilisée pour la rupture de traction transversale et de 0,4 kN/cm² pour la rupture de cisaillement. L’énergie de rupture est issue de [1] (rupture de traction transversale G = 220 N/m, rupture de cisaillement = 780 N/m). Les diagrammes doivent être convertis en effort linéique car les paramètres de matériau ne peuvent pas être entrés directement dans le modèle. Cela nécessite une épaisseur de matériau de 120 mm. Par souci de simplification, les propriétés suivantes sont définies pour la libération de l’articulation : En direction de l’axe local z, le transfert de charge n’est considéré que pour la compression et le long de l’axe x, une charge de 480 kN/m est appliquée.
Conditions aux limites
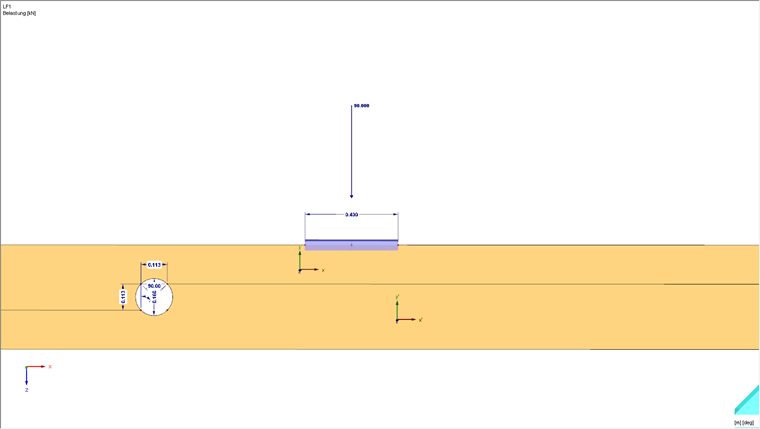
La structure est supportée par des appuis linéiques dans la zone inférieure afin de considérer clairement la largeur d’appui de la structure. De plus, l’un des appuis linéiques peut transférer uniquement les efforts de compression afin de considérer le déplacement unilatéral dans le calcul. Dans les coins supérieurs, la structure est maintenue hors du plan afin de ne pas considérer le renversement dans le calcul.
Chargement
Une charge concentrée de 100 kN est appliquée au centre de la structure. Afin d’éviter d’éventuelles singularités au point d’application de la charge, une barre est utilisée pour la distribution de la charge concentrée dans la surface.
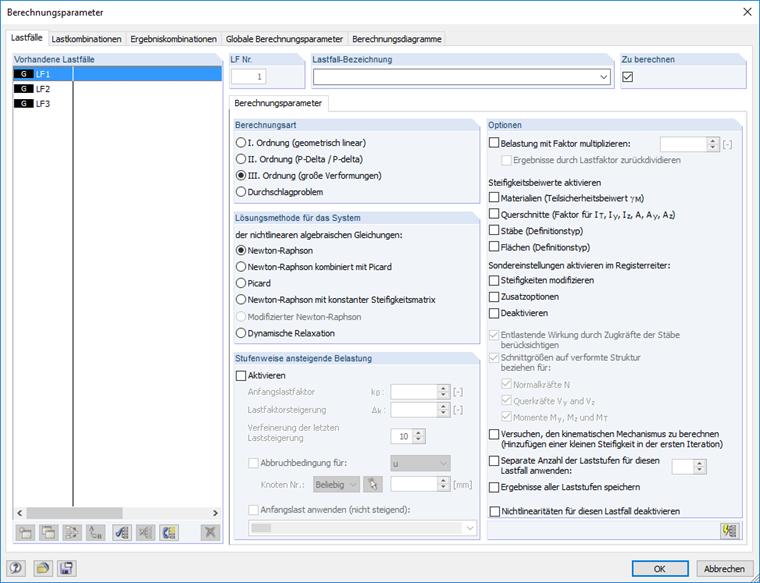
Calcul
En raison du degré non linéaire élevé du modèle, le calcul est effectué selon l’analyse du second ordre. RFEM utilise le solveur de Newton-Raphson, une méthode tangente pour le calcul de l’état d'équilibre. Les paramètres du maillage EF ont été globalement ajustés à 2,5 mm dans le modèle, ce qui permet une évaluation précise des résultats et une meilleure localisation de la zone de rupture (fissuration).
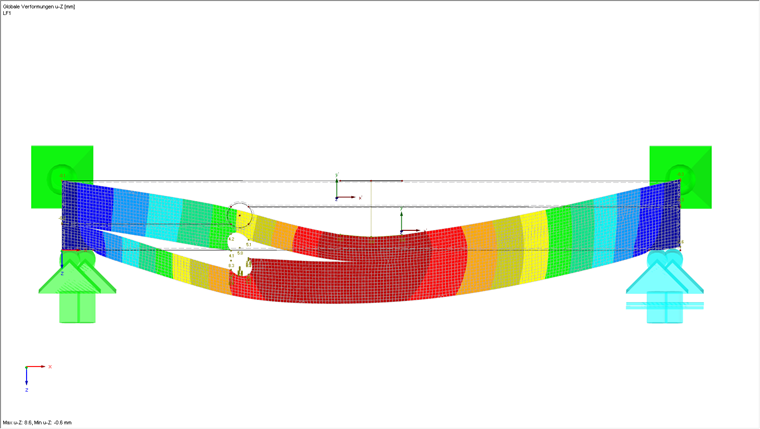
Évaluation
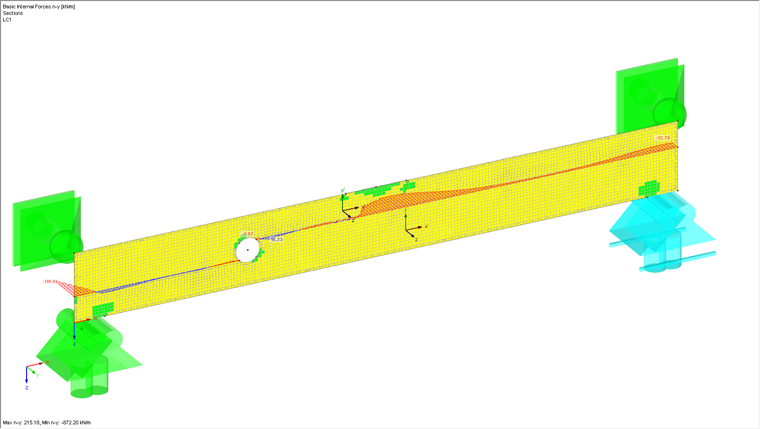
Après le calcul, on constate que la structure se fissure clairement au niveau de la zone de l’ouverture. Si vous placez une coupe sur les ouvertures de fissures, vous obtiendrez des valeurs très faibles pour les efforts internes ny dans cette zone car l’ouverture se produit ici et ainsi aucune charge ne pourra plus être transférée. Ces valeurs flambent ensuite à nouveau dans la zone arrière car l’ouverture des fissures n’y est pas encore disponible et la charge peut être transférée dans cette zone. Cependant, il y a toujours des petites valeurs pour ny dans la zone de fissuration. Elles résultent des contraintes internes de la structure, car la traction transversale peut être complètement exclue en raison de la modélisation dans la zone de fissuration. Cette traction transversale est due à la flexion de la poutre.
Cet exemple illustre la puissance de RFEM dans le domaine des conditions de contact non linéaires (éléments d’interface) et montre que RFEM est également utilisable pour la recherche.