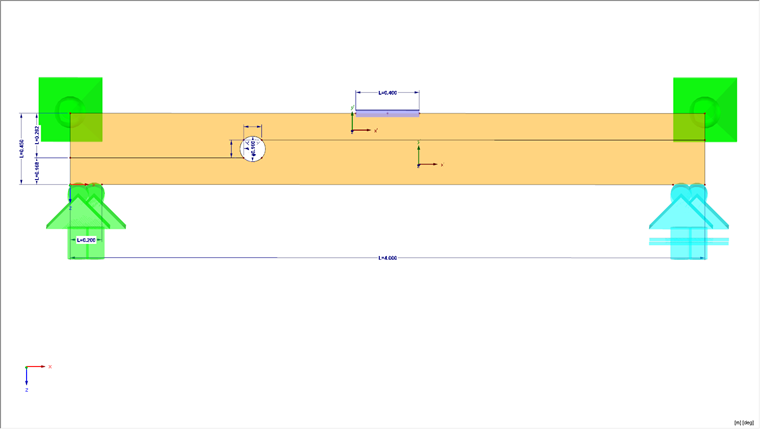
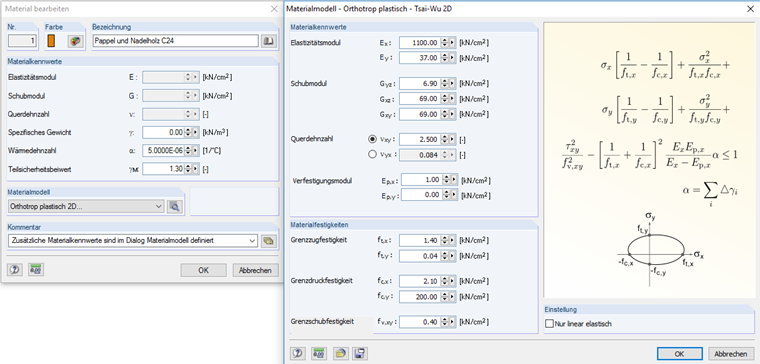
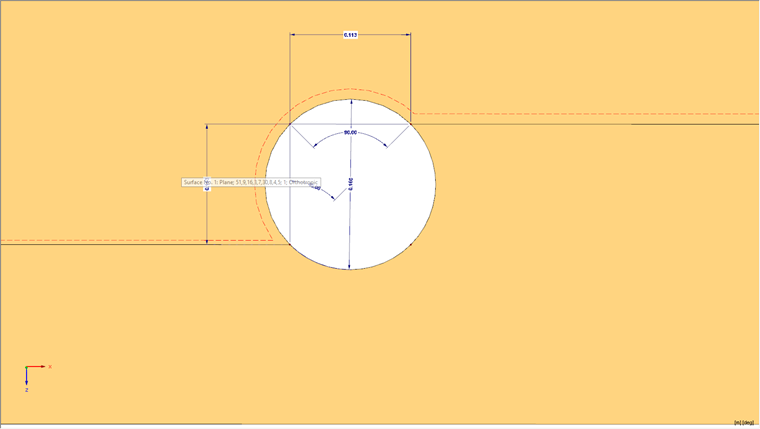
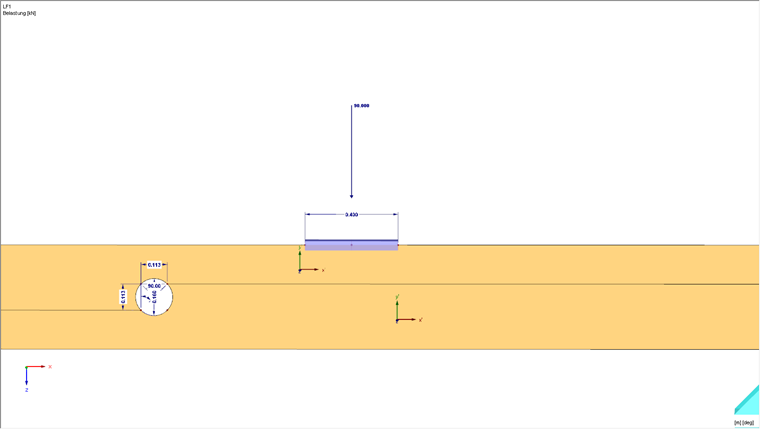
Der Träger soll eine Abmessung von 4.000 mm haben, seine Höhe beträgt 450 mm und die Breite 120 mm. Die Simulation soll mit einem Lochdurchmesser von 0,4 ∙ Trägerhöhe durchgeführt werden. Als Material wird Holz C24 genutzt, als Materialmodell ein orthotropes plastisches Materialmodell, welches den Holzwerkstoff abbildet. Die Simulation des Risses wird mit der sogenannten Linienfreigabe modelliert.
Der zu erwartende Riss im Modell tritt dabei um 45° versetzt zum Mittelpunkt des Kreises auf, am Rand der Öffnung. Der Riss bildet sich entlang der Faser aus, sodass man hier von einem Rollschubversagen sprechen kann. Die Linienfreigabe fungiert als Interface-Element, in dem eine doppelte Linie simuliert wird, welche über Kontakteigenschaften gekoppelt wird. Für die Kontakteigenschaften werden im Modell die Materialeigenschaften nach Abschnitt 4.4 in [1] verwendet. Konkret werden die Materialeigenschaften als Diagramme für die Linienfreigabe im Vorfeld berechnet und anschließend der Linienfreigabe zugeordnet.
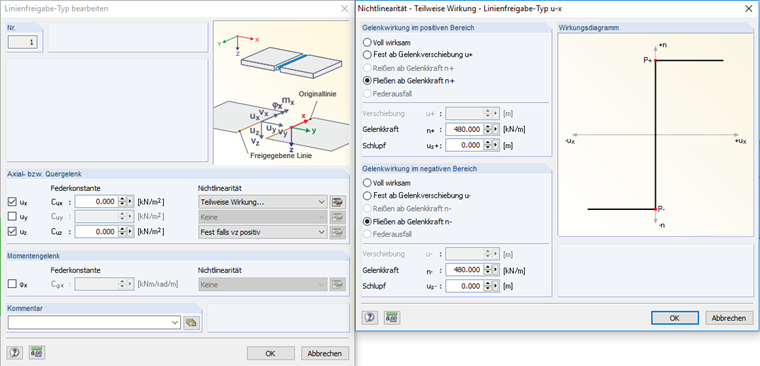
Definition Linienfreigabe
Um nun der Linienfreigabe die Materialeigenschaften zuzuordnen, werden im Programm dafür nichtlineare Gelenkeigenschaften erstellt. Dazu wird in diesem Beispiel mit einem Diagramm gearbeitet. Um den Rollschub richtig zu berücksichtigen, wurde ein Diagramm für das Schubversagen (entlang der lokalen Linienachse x) und ein Diagramm für das Querzugversagen (lokale z Achse der Linie) erstellt. Dabei kann sich das Schubversagen in die positive und negative X-Richtung ausbreiten, wobei das Querzugversagen im Diagramm nur durch Werte im 4. Quadranten beschrieben wird (also Zugversagen). Für das Querzugversagen wird ein Wert von 0,04 kN/cm² verwendet und für das Schubversagen 0,4 kN/cm². Die Bruchenergie wird aus [1] übernommen (Querzugversagen G = 220 N/m, Schubversagen = 780 N/m). Da im Modell die Materialparameter nicht direkt eingeben werden können, müssen die Diagramme auf eine Linienkraft umgerechnet werden. Dafür benötigt man die Dicke des Materials von 120 mm. Vereinfachend werden für die Gelenkfreigabe folgende Eigenschaften definiert. Dabei wird in Richtung der lokalen z-Achse ein Lastübertrag nur auf Druck berücksichtigt und entlang der x-Achse eine Last von 480 kN/m angenommen.
Randbedingungen
Die Struktur wird im unteren Bereich über eine Linienlagerung gelagert, um die Auflagerbreite der Struktur eindeutig zu berücksichtigen. Zudem kann eines der Linienlager nur Druckkräfte aufnehmen, um ein einseitiges Abheben in der Berechnung berücksichtigen zu können. In den oberen Ecken wird die Struktur aus der Ebene gehalten, um ein Kippen in der Berechnung nicht zu berücksichtigen.
Belastung
Die Belastung erfolgt über eine Einzellast von 100 kN, welche in der Mitte der Struktur angesetzt wird. Dabei wird zur Verteilung der Einzellast in die Fläche mit einem Stab gearbeitet, um mögliche Singularitäten im Lasteinleitungspunkt zu vermeiden.
Berechnung
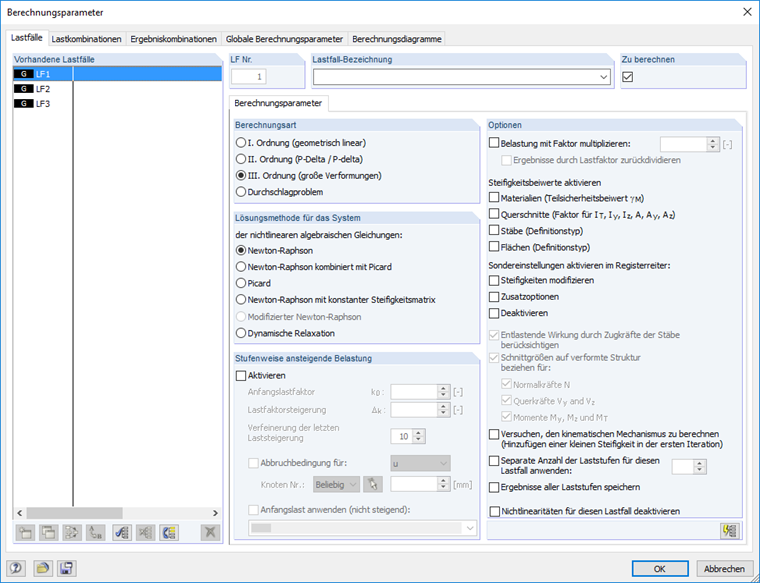
Aufgrund des hohen nichtlinearen Grades des Modells wird die Berechnung auf Theorie III. Ordnung eingestellt. Dabei verwendet RFEM den Newton-Raphson-Solver, also ein Tangentenverfahren zur Berechnung des Gleichgewichtszustandes. Die FE-Netz-Einstellungen sind im Modell global auf 2,5 mm angepasst worden, um eine genauere Ergebnisauswertung durchführen und den Bereich des Versagens (Aufreißen) besser lokalisieren zu können.
Auswertung
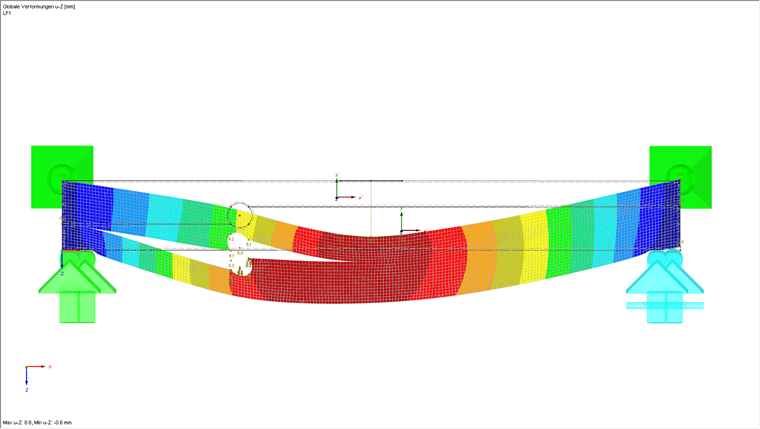
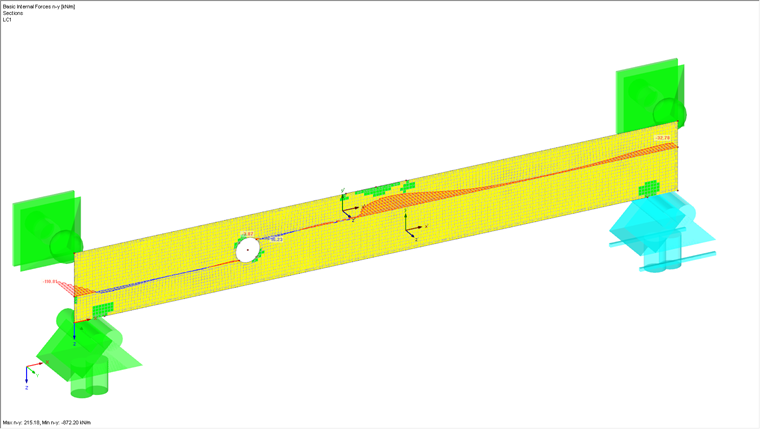
Nach der Berechnung ist ein deutliches Aufreißen der Struktur im Lochbereich zu beobachten. Legt man nun einen Schnitt an die Rissöffnungen, erhält man für die internen Schnittgrößen ny in diesem Bereich sehr kleine Werte, da hier die Öffnung entsteht und damit keine Lasten mehr übertragen werden können. Diese Werte bauchen dann im hinteren Bereich wieder aus, da dort die Rissöffnung noch nicht vorhanden ist und die Last in diesem Bereich abgeleitet werden kann. Im Rissbereich sind aber immer noch kleine Werte für ny vorhanden. Diese resultieren aus der Eigenspannung der Struktur, da ein Querzug aufgrund der Modellierung im Rissbereich nicht komplett ausgeschlossen werden kann. Dieser Querzug entsteht aufgrund der Biegung des Balkens.
Dieses Beispiel verdeutlicht, wie leistungsstark RFEM auch im Bereich nichtlinearer Kontaktbedingungen (Interface-Elemente) ist und dass RFEM auch in der Forschung einsetzbar ist.