cálculo das forças de apoio
Primeiro, deve ficar claro como é determinado o resultado de um apoio de linha. Um apoio de linha é dividido internamente em apoios nodais em cada ponto da malha. De seguida, é determinada uma força de apoio para cada apoio nodal. Através de determinadas opções de suavização que têm em consideração a influência dos apoios adjacentes, é criada a distribuição linear entre os pontos de apoio individuais (nodais). Este resultado corresponde à distribuição real.
Ao considerar uma placa quadrada com carga constante em ambos os lados como um exemplo simples, já se pode ver que o número de elementos finitos bem como a rigidez da placa utilizada (espessura, coeficiente de Poisson, isotrópico ou ortotrópico) e a rigidez de o apoio desempenham um papel importante.
Exemplo 1: carga de superfície constante
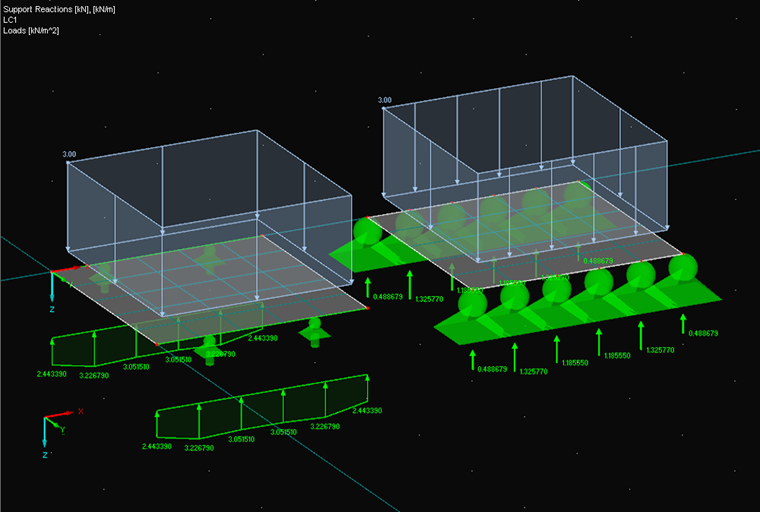
Uma laje de 20 cm de espessura com as dimensões 2 · 2 m e uma largura de malha de EF de 40 cm é carregada por uma carga de superfície de 3 kN/m². A relação de Poisson foi assumida como 0. O modelo foi introduzido uma segunda vez com apoios nodais.
A distribuição das forças de apoio de linha é determinada com as reações de apoio nodais determinadas, a largura de influência e a opção de suavização. Nos pontos de borda, a largura de influência corresponde a 20 cm (= metade da largura da malha EF) e dentro 40 cm (= largura total da malha de EF).
K1 = 0,488678 → L1 = 0,488678/0,2 = 2,44339 kN/m
K2 = 1,325770 → L2 = (1,325770 · 3 + 1,185550)/4/0,4 = 3,2267875 kN/m
K3 = 1,185550 → L3 = (1,185550 · 2 + 1,325770 + 1,185550)/4/0,4 = 3,0515125 kN/m
K4 = 1,185550 → L4 = (1,185550 · 2 + 1,185550 + 1,325770)/4/0,4 = 3,0515125 kN/m
K5 = 1,325770 → L5 = (1,325770 · 3 + 1,185550)/4/0,4 = 3,2267875 kN/m
K6 = 0,488678 → L6 = 0,488678/0,2 = 2,44339 kN/m
Exemplo 2: apoio nodal adicional
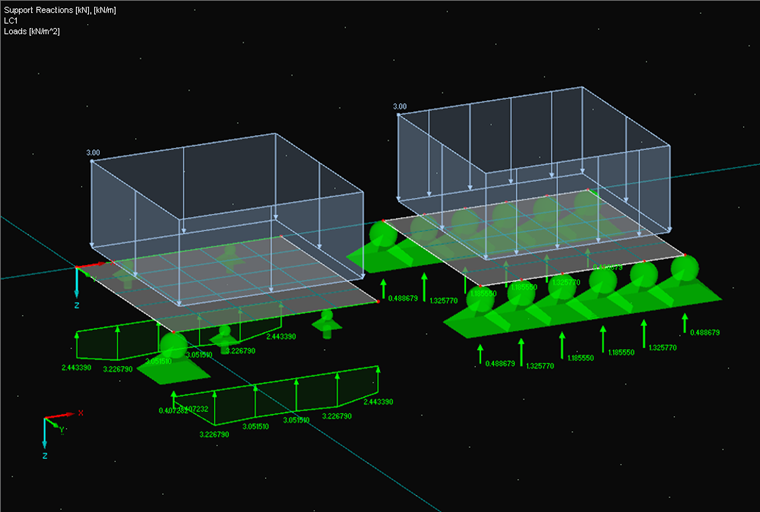
Tal como no exemplo 1, mas é inserido um apoio nodal adicional no início do apoio de linha. É exibida uma mensagem de aviso correspondente antes do cálculo. Além do nó adicionalmente apoiado, não existem diferenças. Como a carga total no nó 1 deve ser o valor do exemplo acima e os dois apoios têm a mesma rigidez, resulta no valor seguinte para o apoio nodal e a coordenada inicial do apoio.
K1 = L1
K1 + 0,2 · K1 = 0,751475 → K1 = 0,488678/1,2 = 0,4072317 kN e kN/m
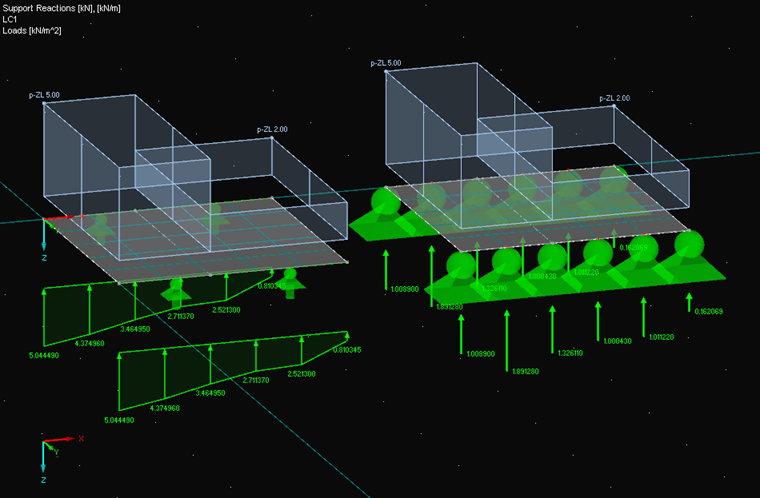
Exemplo 3: duas cargas de bloco diferentes
K1 = 1,008900 → L1 = 1,008900/0,2 = 5,044500 kN/m
K2 = 1,891280 → L2 = (1,891280 · 3 + 1,3326110)/4/0,4 = 4,374969 kN/m
K3 = 1.326110 → L3 = (1.326110 · 2 + 1.891280 + 1.000430)/4/0.4 = 3.464956 kN/m
K4 = 1.000430 → L4 = (1.000430 · 2 + 1,3326110 + 1,011220)/4/0,4 = 2,711369 kN/m
K5 = 1,011220 → L5 = (1,011220 · 3 + 1.000430)/4/0,4 = 2,521306 kN/m
K6 = 0,162069 → L6 = 0,162069/0,2 = 0,810345 kN/m
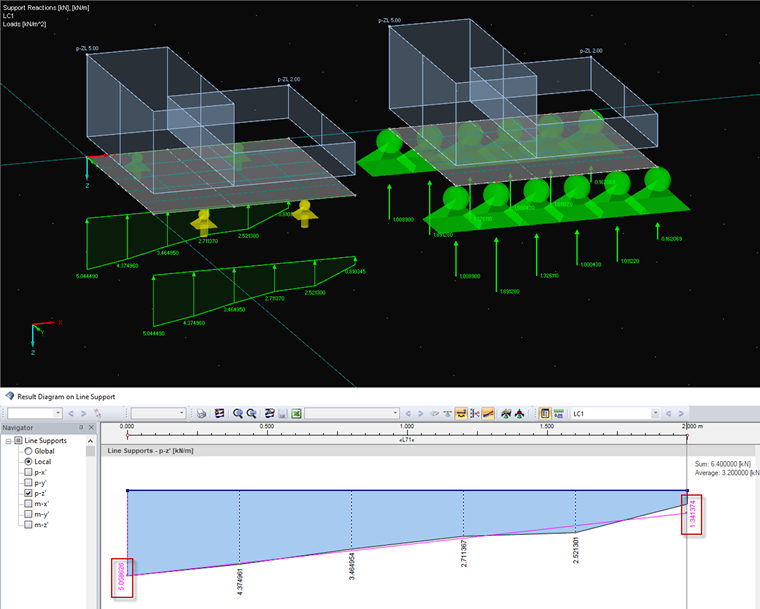
Exemplo 4: suavização linear com o exemplo 3
O programa tem de determinar um trapézio com a mesma integral e as mesmas coordenadas do centro de gravidade como a cadeia poligonal exibida. Para a determinação da superfície (corresponde à soma da carga), é menos importante quão grosseira é malha de EF, mas é menos importante para a determinação das coordenadas do centro de gravidade. Além disso, a inclinação do gradiente suavizado deve seguir as ordenadas do gradiente real. É semelhante ao cálculo da linha de tendência linear no Excel. Primeiro, são determinadas as integrais das áreas parciais individuais.
A1 = (5,044500 + 4,374969)/2 0,4 = 1,8838938 kN
A2 = (4,374969 + 3,464956)/2 0,4 = 1,5679850 kN
A3 = (3,464956 + 2,711369)/2,4 0,4 = 1,2352650 kN
A4 = (2,711369 + 2,521306)/2 0,4 = 1,0465350 kN
A5 = (2,521306 + 0,810345)/2 · 0,4 = 0,66663302 kN
Soma das forças de apoio da linha = 6,400009 kN
Os centros de gravidade locais das áreas parciais individuais são:
xs1 = 0,4/3 · ((5,044500 + 2 · 4,374969)/(5,044500 + 4,374969)) = 0,195261366 m
xs2 = 0,4/3 · ((4,374969 + 2 · 3,464956)/(4,374969 + 3,464956)) = 0,192261724 m
xs3 = 0,4/3 · ((3,464956 + 2 · 2,711369)/(3,464956 + 2,711369)) = 0,191865848 m
xs4 = 0,4/3 · ((2,711369 + 2 · 2,521306)/(2,711369 + 2,521306)) = 0,197578517 m
xs5 = 0,4/3 · ((2,521306 + 2 · 0,810345)/(2,521306 + 0,810345)) = 0,156763498 m
Posteriormente, o centro de gravidade global é determinado pela multiplicação dos integrais parciais pelo centro de gravidade global no início da linha e pela divisão da carga total.
(A1 · xs1 + A2 · (xs2 + 0,4) + A3 · (xs3 + 2 · 0,4) + A4 · (xs4 + 3 · 0,4) + A5 · (xs5 + 4 · 0,4))/6,400009 = 0,806393054 m
Agora, apenas é necessário determinar os dois comprimentos de borda da superfície trapezoidal que têm a mesma posição do centro de gravidade. Isto é feito através da conversão do cálculo do centro de gravidade e do cálculo da força de apoio total.
b = (0,806393054 · 3/2 - 1)/(2 - 0,806393054 · 3/2) = 0,265165508 a
a = (6,400009 · 2/2)/(1 + 0,265165508) = 5,05863 kN/m → b = 1,34137
Nota
Os exemplos apresentados neste artigo foram calculados com uma malha de EF irregular, de modo a permitir que o procedimento possa ser ilustrado com exemplos. Com a opção "Diagramas de resultados" no menu de atalho do apoio de linha, apenas o diagrama linear com as suas ordenadas nos pontos de apoio (sem a informação na janela de informação) é transferido para a caixa de diálogo aberta. Portanto, a suavização linear na caixa de diálogo mostra uma suavização linear ligeiramente diferente da da janela de trabalho. Se o tamanho da malha de EF é reduzido cada vez mais, de modo que a distribuição poligonal se adapte cada vez mais a uma distribuição curva, são cometidos erros cada vez mais pequenos ao integrar a superfície e determinar o centro de gravidade.