Bei sehr großen Modellen mit sehr vielen Freiheitsgraden oder bei Strukturen, die fundamentale Eigenwerte im hochfrequenten Bereich aufweisen (zum Beispiel Rohrleitungssysteme), sind diese Forderungen unter Umständen schwer zu erfüllen. In solchen Fällen gewinnt die ZPA-Methode (Zero-Period-Acceleration) an Bedeutung. Este método también es capaz de considerar las masa en los apoyos por sí mismas, lo cual tiene una influencia decisiva en las fuerzas en los apoyos.
Man unterscheidet drei Frequenzbereiche, anhand welcher die Systemantworten unterschiedlich kategorisiert werden können (siehe Bild 01): (1) Niedrigfrequenzbereich, (2) Mittelfrequenzbereich und (3) der hochfrequente Bereich.
El intervalo de baja y media frecuencia (f < fZPA), son los intervalos considerados normalmente en la dinámica estructural. Bauwerke besitzen dominante Eigenfrequenzen in diesem Bereich und in vielen Fällen werden mehr als 90 % der Strukturmasse mit diesen Eigenwerten aktiviert. Die Systemantworten im niederfrequenten Bereich sind periodisch und Ergebnisse von verschiedenen Eigenwerten sind phasenverschoben. Die Überlagerung der Antworten aus einzelnen Eigenwerten erfolgt quadratisch entweder mit der SRSS- oder besser mit der CQC-Regel.
El intervalo de frecuencia alta (f > fZPA), las respuestas del sistema son pseudo estáticas y las respuestas desde los valores propios individuales están en fase. Die modale Überlagerung kann somit als algebraische Summe ausgeführt werden. Anstatt diese Hochfrequenzen dynamisch zu berücksichtigen, ist es üblich, die fehlenden aktivierten Massen zu ermitteln und mittels des ZPA-Wertes die Antworten des gesamten hochfrequenten Bereiches pseudo-statisch hinzuzufügen. El valor de ZPA se corresponde con el valor del espectro de respuesta para el período T = 0 segundos; ZPA = Sa (T = 0). Es ist aber auch ein selbst definierter Wert für den ZPA-Wert vorstellbar. Este método se llama ZPA, método de las masas omitidas o también corrección estática [2, 3, 4].
Las frecuencias del intervalo medio (fSP < f < fZPA) proporcionan respuestas del sistema que son periódicas y pseudo estáticas a las partes. Estas frecuencias se pueden combinar con las reglas de superposición especiales tales como el método Gupta [2] para considerar la suma algebráica de las componentes pseudo estáticas. Eine Überlagerung mittels üblicher quadratischer Regeln wie der CQC-Regel ist aber ebenfalls üblich.
La frecuencia fSP (sp = "spectral peak" o pico del espectro) se corresponde con el valor máximo de la aceleración del espectro. La frecuencia fZPA (ZPA = "Zero-Period-Acceleration" o aceleración del periodo cero) es la frecuencia mínima con la que la aceleración alcanza aproximadamente el valor ZPA.
Berechnung der ZPA-Anteile
Die Anteile der aktivierten Massen an jedem einzelnen Knoten im System können wie folgt ermittelt werden:
Donde
i = 1...p = Anzahl der Eigenwerte die im Antwortspektrenverfahren berücksichtigt werden
j = dirección del movimiento sísmico
mj = (mX,j, mY,j, mZ,j) = partes de las masas activadas en cada nodo en la dirección de excitación j
Γij = Beteiligungsfaktoren für den Eigenwert i und die Anregungsrichtung j
ui = (uX, uY, uZ)T =modo propio del valor propio i en un solo nodo, masa normalizada con Mi = uiT ∙ M ∙ ui = 1 kg
Der Anteil der fehlenden, nicht aktivierten Massen an jedem einzelnen Knoten, ist die Differenz zur gesamten Strukturmasse und wird wie folgt bestimmt:
mj,missing = 1 - mj
Die Ersatzlasten an jedem Knoten und daraus folgend dann Verformungen und Schnittgrößen für den Anteil der nicht aktivierten Massen ermitteln sich folgendermaßen:
Fj = mj,missing ∙ ZPAj ∙ M
Donde
Fj = (FX,j, FY,j, FZ,j) = cargas equivalentes en cada nudo para la proporción de masas desactivadas que resultan de la dirección de excitación j
ZPAj = aceleración espectral Sa,j(T=0) en la dirección de la excitación j
M = (MX, MY, MZ) = masa en los nudos individuales del sistema
Die so ermittelten Ergebnisse der ZPA-Anteile werden bei der modalen Überlagerung wie ein weiterer Eigenwert behandelt. La superposición con los resultados de los valores propios considerados dinámicamente se pueden realizar mediante la regla SRSS o una suma absoluta. Die absolute Summe liefert auf der sicheren Seite liegende Ergebnisse.
Umsetzung in DYNAM Pro - Erzwungene Schwingungen
In DYNAM Pro - Erzwungene Schwingungen wird die ZPA-Methode angewendet, wenn das Kontrollkästchen "Statische Korrektur anwenden" selektiert ist. El ajuste se muestra en la Figura 02.
In DYNAM Pro erfolgt die Ermittlung der nicht aktivierten Massen und der daraus resultierenden Ersatzlasten intern. El valor ZPA se define con el valor desde el espectro de respuesta para el periodo T = 0 segundos, ZPA = Sa (T = 0). Los resultados de la componente ZPA están superpuestos como una suma absoluta con los resultados de los valores propios considerados de forma dinámica.
Rt = |RSRSS/CQC| + |Rmissing|
Donde
Rt = resultados después de la superposición modal y direccional, incluyendo la componente ZPA
RSRSS/CQC = resultados de los valores propios considerados de forma dinámica, modalmente superpuestos con la regla SRSS o CQC
Rmissing = resultados del componente ZPA
Die Ergebnisse nach erfolgter Überlagerung werden als Ergebniskombination in das Hauptprogramm RSTAB exportiert.
Ejemplo
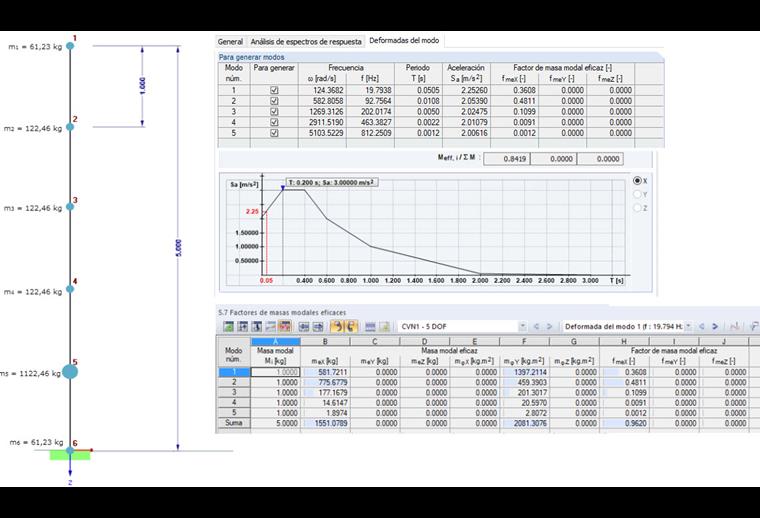
An einem Kragarm mit fünf Freiheitsgraden wird aufgezeigt, wie die ZPA-Methode in DYNAM Pro - Erzwungene Schwingungen umgesetzt ist. Betrachtet wird ein sehr einfaches System, um die Nachvollziehbarkeit der Ergebnisse zu ermöglichen. Se selecciona una sección rígida RO 508,0x10,0508.0x10,0 con Iy508.0x10.0 = 508.0x10.048,520 cm4 hechos de acero S 235 para alcanzar las frecuencias superiores al valor fZPA con la contribución de masa relevante. Das Eigengewicht des Trägers von 612,3 kg wird gleichmäßig auf die sechs Knoten (inklusive Auflagerknoten) verteilt. Además, se define una masa de 1 t en el nudo 5. Die Massen und auch die Anregung des Systems wirken in X-Richtung. Die Struktur mit Masseverteilung, resultierenden Eigenfrequenzen und effektiven Modalmassen ist zusammen mit dem benutzerdefinierten Antwortspektrum in Bild 03 dargestellt.
En este ejemplo, el valor de ZPA es Sa = 2,00 m/s2. Este es el valor de aceleración para el período T = 0 seg. Si el espectro de respuesta se traza contra las frecuencias, el valor límite da como resultado una frecuencia de fZPA de 100 Hz. Las dos primeras frecuencias f1 = 19,8 Hz y f2 = 92,8 H< de este modo se encuentran en el intervalo de frecuencia media (ver figura 01) y se consideran de forma dinámica. Die restlichen drei Eigenfrequenzen sind hochfrequent und können mit der ZPA-Methode berücksichtigt werden.
Als Standardeinstellung werden bei der Eigenwertberechnung in DYNAM Pro die Massen an festen Auflagern nicht berücksichtigt. Diese Massen haben keinen Einfluss auf die ermittelten Eigenfrequenzen und nur so ist es möglich, effektive Modalmassenfaktoren von 100 % zu erzielen.
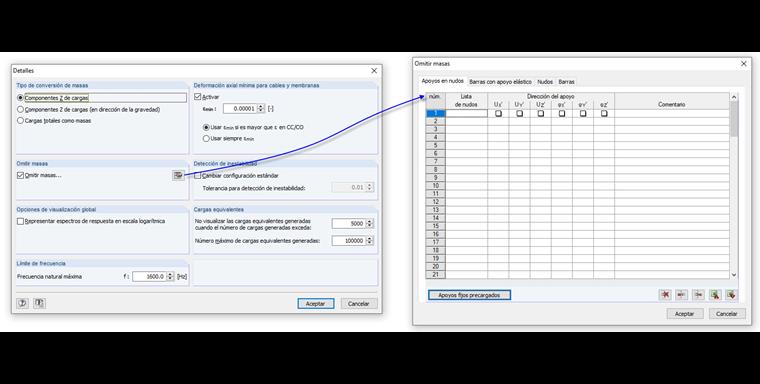
Wenn man bei der ZPA-Methode aber explizit den Einfluss der Massen in den Auflagern mitberücksichtigen möchte, muss man diese in DYNAM Pro mit der in Bild 04 gezeigten Einstellung aktivieren. In diesem Beispiel werden die Massen in den Auflagern berücksichtigt.
Durch Aktivierung von "Massen vernachlässigen" werden die Standardeinstellung der berücksichtigten Massen geändert. Lässt man die Tabelle der "Knotenlager" leer, werden Massen auch an Auflagern berücksichtigt.
La siguiente tabla determina los factores de participación ΓX, las proporciones de las masas activadas mX. las proporciones de las masas desactivadas mX, missing y las cargas equivalentes resultantes en los seis nudos del sistema. Die Berechnungsgrundlagen der ZPA-Methode wurden im vorherigen Abschnitt diskutiert.
| Nudos | Masa Mx | factor de participación ΓX | Deformada del modo uX | Anteile der activado Masas mx | Anteile der fehlenden Masas mX,missing | Cargas equivalentes FX [N] | ||
| Forma 1 | Forma 2 | Forma 1 | Forma 2 | |||||
| 1 | 61,23 | 0,078350 | -0,056290 | 0,3220 | 0,6780 | 83,03 | ||
| 2 | 122,46 | 0,056790 | -0,008520 | 1,1325 | -0,1325 | -32,44 | ||
| 3 | 122,46 | 24,12 | 27,85 | 0,036140 | 0,027190 | 1,6290 | -0,6290 | -154,05 |
| 4 | 122,46 | 0,018110 | 0,038290 | 1,5033 | -0,5033 | -123,26 | ||
| 5 | 1 122,46 | 0,005100 | 0,021670 | 0,7266 | 0,2734 | 613,82 | ||
| 6 | 61,23 | 0,000000 | 0,000000 | 0,0000 | 1,0000 | 122,46 | ||
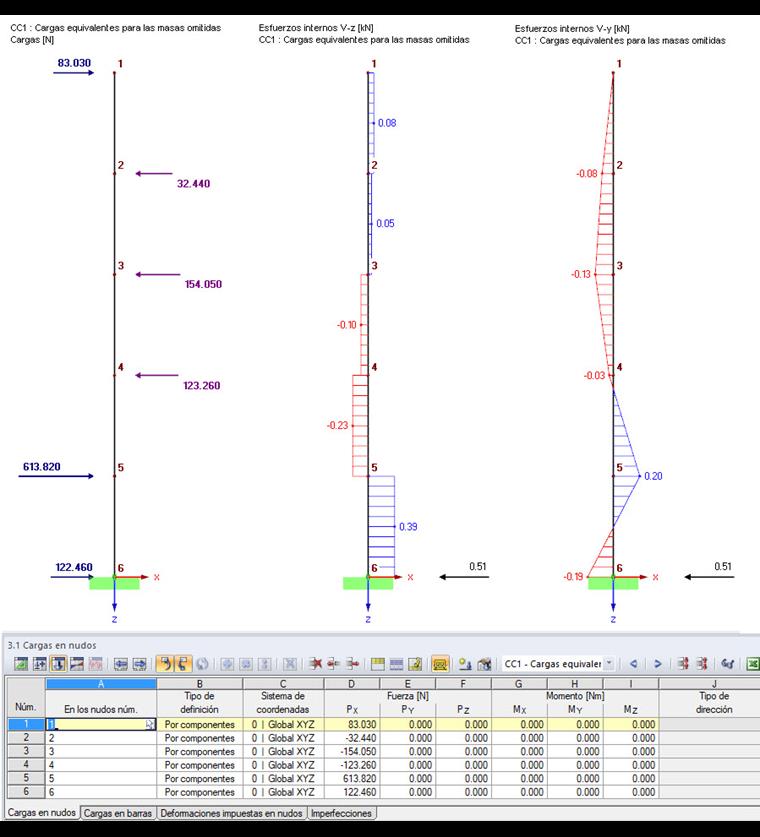
Die Querkräfte, Momente und Auflagerkräfte resultierend aus diesen Ersatzlasten sind in Bild 05 dargestellt.
Die Endergebnisse des multi-modalen Antwortspektrenverfahrens unter Berücksichtigung der ZPA-Methode ergeben sich aus den Ergebnissen der ersten beiden Eigenwerte (hier modal überlagert mit der SRSS-Regel) und den Ergebnissen des ZPA-Anteiles (siehe Bild 05).
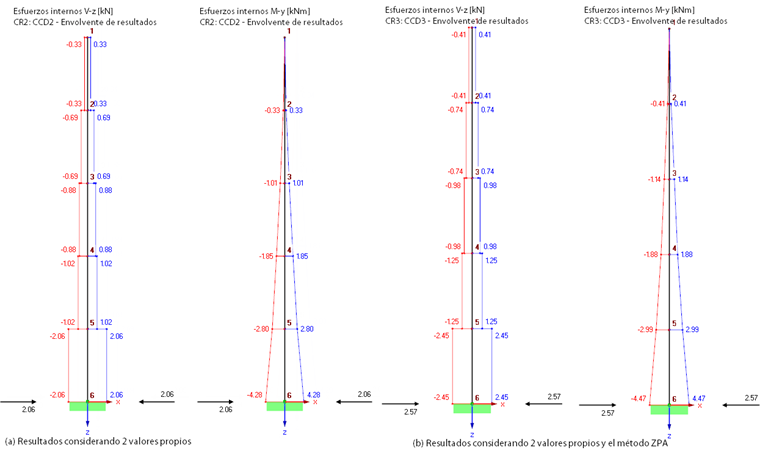
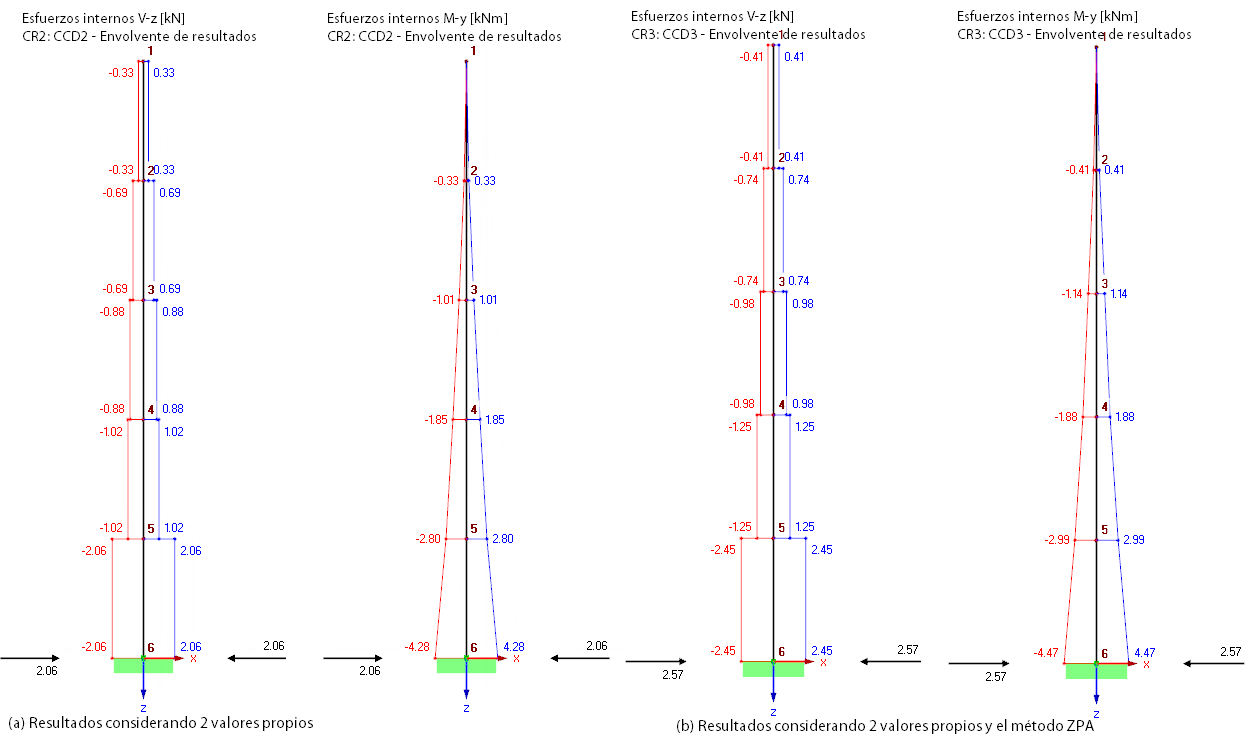
In Bild 06 sind die Ergebnisse des Antwortspektrenverfahrens unter Berücksichtigung der ersten beiden Eigenwerte (DLF2 und EK2 im Modell) den finalen Ergebnissen inklusive dem ZPA-Anteil (DLF3 und EK3 im Modell) gegenübergestellt. Betrachtet man Bild 05 und Bild 06, ist die absolute Summenbildung, die in DYNAM Pro Verwendung findet, klar zu erkennen.
In Bild 07 sind die Ergebnisse des Antwortspektrenverfahrens unter Berücksichtigung aller fünf Eigenwerte zum Vergleich dargestellt. Die ZPA-Methode berücksichtigt die Massen in den Auflagern. Esto da como resultado una fuerza en el apoyo mayor, de PX = 2,57 kN. Die Schnittgrößen liegen auf der sicheren Seite aufgrund der Überlagerung als absolute Summe (vergleiche Bild 07 mit Bild 06).
Resumen
Mit diesem Beispiel wurde gezeigt, wie die ZPA-Methode in DYNAM Pro umgesetzt ist und dass die Ergebnisse prüfbar nachvollziehbar sind. Sinnvoll und empfohlen ist diese Methode, wenn hochfrequente Frequenzen der Struktur relevante Massenanteile aktivieren und wenn größere Auflagermassen im Bauwerk vorhanden sind.
![Spektrale Beschleunigung Sa [m/s²] versus Eigenfrequenz f [Hz] eines schmalbandigen Antwortspektrums nach EN 1998-1 [1]](/es/webimage/009251/2417758/01-es_kb001511-jpg.jpg)