Dans le cas de structures importantes ayant de nombreux degrés de libertés, ou de structures dont la valeur propre fondamentale est dans les hautes fréquences (systèmes de canalisation, par exemple), il peut être difficile de satisfaire ces exigences. Pour de tels cas, la méthode ZPA (Zero-Period-Acceleration) gagne en importance. Cette méthode permet également de considérer des masses au niveau des appuis eux-mêmes, ce qui a une influence décisive sur les forces d’appui.
Une distinction est faite entre trois gammes de fréquence, avec lesquels les réponses du systèmes sont catégorisées de différentes manières (voir la Figure 01) : (1) Gamme de basse fréquence, (2) Gamme de fréquence moyenne et (3) Gamme de haute fréquence.
Les gammes de fréquence basse et moyenne (f < fZPA) sont les gammes les plus souvent considérées dans le cadre de l’analyse dynamique. Les fréquences propres dominantes des bâtiments se trouvent dans cette gramme, et dans de nombreux cas, plus de 90 % de la masse de la structure est activée avec ces valeurs propres. Les réponses système dans la gamme de basse fréquence sont périodiques et les résultats des différentes valeurs propres sont déphasés. La superposition des réponses des valeurs propres individuelles est effectuée de manière quadratique, soit à l’aide de la règle SRSS, soit à l’aide de la règle CQC.
Dans la gamme de haute fréquence (f > fZPA), les réponses système sont pseudo-statiques, les réponses des valeurs propres individuelles sont de même phase. La superposition modale peut ainsi être exécutée comme somme algébrique. Plutôt que de considérer ces hautes fréquences dynamiquement, il est habituel de déterminer les masses activées manquantes et d’ajouter pseudo-statiquement les réponses de la structure totale à l’aide des valeurs ZPA. La valeur ZPA correspond à la valeur du spectre de réponse pour la période T = 0 sec; ZPA = Sa(T=0). La valeur ZPA peut cependant être définie par l’utilisateur. Cette méthode est appelée méthode ZPA, méthode de la masse manquante ou correction statique [2, 3, 4].
Les fréquences moyennes (fSP < f < fZPA) donnent des réponses système partiellement périodiques et partiellement pseudo-statique. Ces fréquences peuvent être combinées avec des règles de superposition spéciales, comme par exemple la méthode Gupta [2], afin de considérer la somme algébrique des composants pseudo-statiques. Une superposition à l’aide des règles quadratique standard, telles que CQC, est cependant également habituelle.
La fréquence fSP (sp = spectral peak) correspond à la valeur maximale de l’accélération spectrale. La fréquence ZPA fZPA (ZPA = Zero-Period-Acceleration) est la fréquence minimale avec laquelle l’accélération s’approche de la valeur ZPA.
Calcul des composants ZPA
Les composants des masses activées à chaque nœud individuel dans la structure peuvent être déterminés comme suit :
où
i = 1...p = Nombre de valeurs propres considérées dans l’analyse du spectre de réponse
j = Direction de l’excitation sismique
mj = (mX,j, mY,j, mZ,j) = Quantité des masses activées à chaque nœud dans la direction d’excitation j
Γij = Facteurs de participation pour la valeur propre i et la direction d’excitation j
ui = (uX, uY, uZ)T = Mode propre de la valeur propre i à un nœud individuel, masse normalisée avec Mi = uiT ∙ M ∙ ui = 1 kg
La fraction de masses manquantes non activées à chaque nœud individuel est la différence par rapport à la masse structurale totale, et est déterminée comme suit :
mj,missing = 1 - mj
Les charges équivalentes à chaque nœud, et ensuite, les déformations et les efforts internes pour le ratio de masses non activées, sont déterminées comme suit :
Fj = mj,missing ∙ ZPAj ∙ M
où
Fj = (FX,j, FY,j, FZ,j) = Charges équivalentes à chaque nœud pour le ratio de masses non activées, résultant de la direction d’excitation j
ZPAj = accélération spectrale Sa,j(T=0) dans la direction d’excitation j
M = (MX, MY, MZ) = Masse aux nœuds individuels dans la structure
Les résultats des composants ZPA ainsi déterminés sont traités comme une valeur propre supplémentaire lors de la superposition modale. La superposition avec les résultats des valeurs propres déterminées dynamiquement peut s’effectuer à l’aide de la règle SRSS ou comme somme absolue. La somme absolue donne des résultats prudents.
Réalisation dans DYNAM Pro - Forced Vibrations
DYNAM Pro - Forced Vibrations utilise la méthode ZPA si la case « Appliquer la correction statique est cochée » est cochée. Le paramétrage est affiché dans la Figure 02.
Dans DYNAM Pro, la détermination des masses non activées et les charges équivalentes résultantes est effectuée en interne. La valeur ZPA est définie avec la valeur du spectre de réponse à la période T = 0 sec; ZPA = Sa(T=0). Les résultats du composant ZPA sont superposés comme somme absolue avec les résultats des valeurs propres considérées dynamiquement.
Rt = |RSRSS/CQC| + |Rmissing|
où
Rt = Résultats après superposition modale et directionnelle, composant ZPA inclus
RSRSS/CQC = Résultats des valeurs propres considérées dynamiquement avec superposition modale à l’aide de la règle SRSS ou CQC
Rmissing = Résultats du composant ZPA
Les résultats après superposition sont exportés comme combinaison de résultats dans le logiciel principal RSTAB.
Exemple
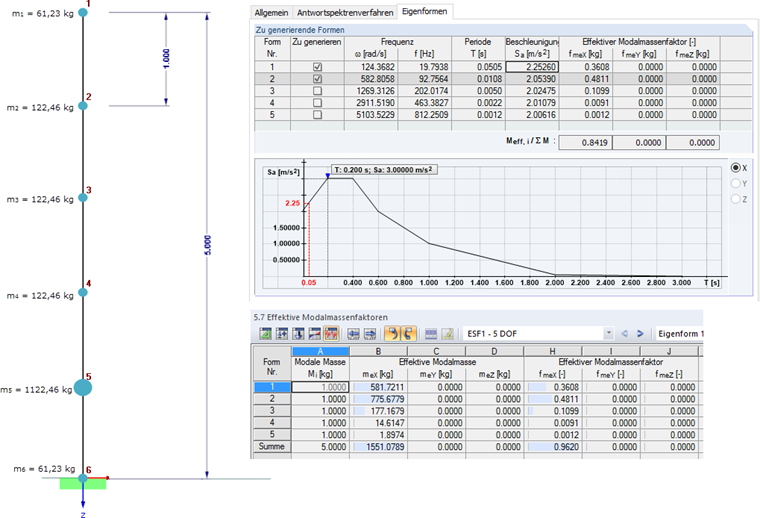
Un porte-à-faux avec cinq degrés de liberté permet d’afficher la mise en œuvre de l’analyse ZPA dans DYNAM Pro - Forced Vibrations. Pour permettre la traçabilité des résultats, un système très simple est considéré. Une section rigide RO 508,0x10,0 mit Iy = 48.520 cm4 en acier S235 est sélectionnée afin d’atteindre des fréquences au-delà de la valeur fZPA avec la participation de masse correspondante. Le poids propre de la poutre (612,3 kg) est distribué uniformément sur les six nœuds (nœuds d’appui compris). De plus, une masse de 1 t est définie au nœud 5. Les masses et les excitations du système agissent en direction X. La structure avec distribution masse, fréquences propres résultantes et masse modale effectives est affichée dans la Figure 03 avec les spectres de réponse définis par l’utilisateur.
Dans cet exemple, la valeur ZPA est de Sa = 2,00 m/s2. C’est la valeur d’accélération pour la période T=0 sec. Si le spectre de réponse est comparé avec les fréquences, la fréquence fZPA avec 100 Hz résulte de la considération des valeurs limites. Les deux premières fréquences f1 = 19,8 Hz et f2 = 92,8 Hz sont ainsi dans la gamme de fréquence moyenne (voir la Figure 01) et sont considérées dynamiquement. Les trois fréquences propres restantes sont des hautes fréquences et doivent être considérées avec la méthode ZPA.
Par défaut, le calcul de valeur propre dans DYNAM Pro ne considère pas les masses pour les appuis fixes. Ces masses n’ont pas d’influence sur les fréquences propres déterminées, et seulement dans ce cas, les facteurs de masse modale effective de 100 % peuvent être atteints.
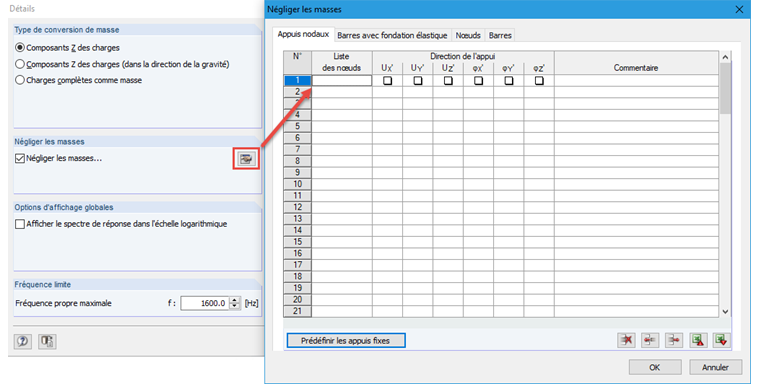
Cependant, si l’influence des masses doit être explicitement considérée aux appuis avec la méthode ZPA, elles doivent être activées dans DYNAM Pro, à l’aide des paramètres de la Figure 04. Dans cet exemple, les masses sont considérées aux appuis.
Activer l’option « Négliger les masses » change le réglage par défaut des masses considérées. Si le tableau des « appuis nodaux » est vide, les masses sont également considérées aux appuis.
Le tableau suivant montre les facteurs de participationΓX, les composants des masses activéesmX, les composants des masses non activéesmX,missing et les masses équivalentes résultantes aux six nœuds du système. Les bases de calcul de la méthode ZPA ont été traitées dans la section précédente.
| Nœuds | Masse Mx | Facteur de participation ΓX | Mode propre uX | Composants des masses activées mX | Composants des masses manquantes mX,missing | Charges équivalentes FX [N] | ||
| Mode 1 | Mode 2 | Mode 1 | Mode 2 | |||||
| 1 | 61,23 | 0,078350 | -0,056290 | 0,3220 | 0,6780 | 83,03 | ||
| 2 | 122,46 | 0,056790 | -0,008520 | 1,1325 | -0,1325 | -32,44 | ||
| 3 | 122,46 | 24,12 | 27,85 | 0,036140 | 0,027190 | 1,6290 | -0,6290 | -154,05 |
| 4 | 122,46 | 0,018110 | 0,038290 | 1,5033 | -0,5033 | -123,26 | ||
| 5 | 1.122,46 | 0,005100 | 0,021670 | 0,7266 | 0,2734 | 613,82 | ||
| 6 | 61,23 | 0,000000 | 0,000000 | 0,0000 | 1,0000 | 122,46 | ||
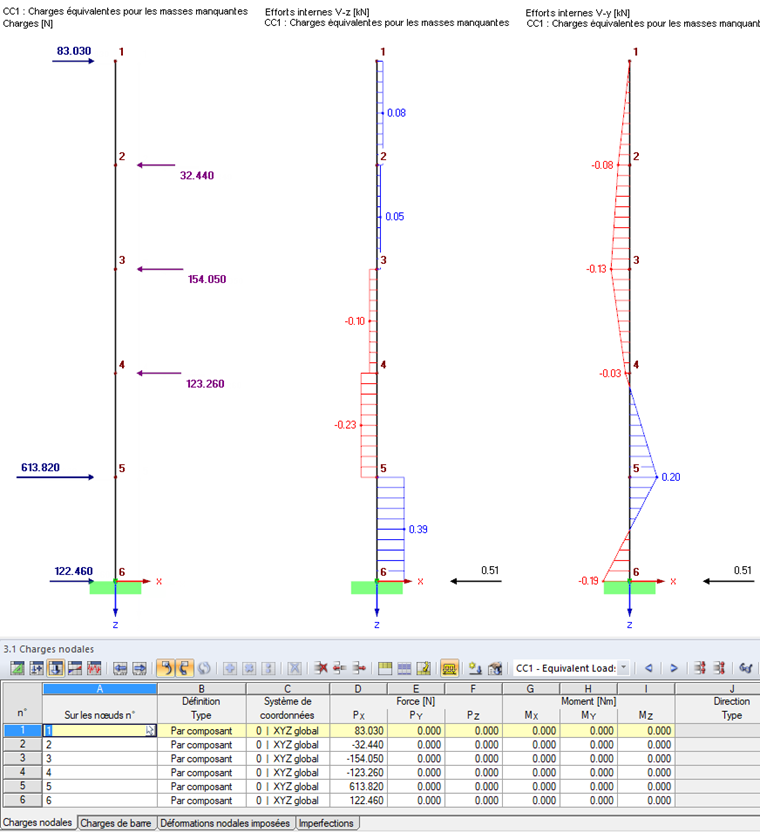
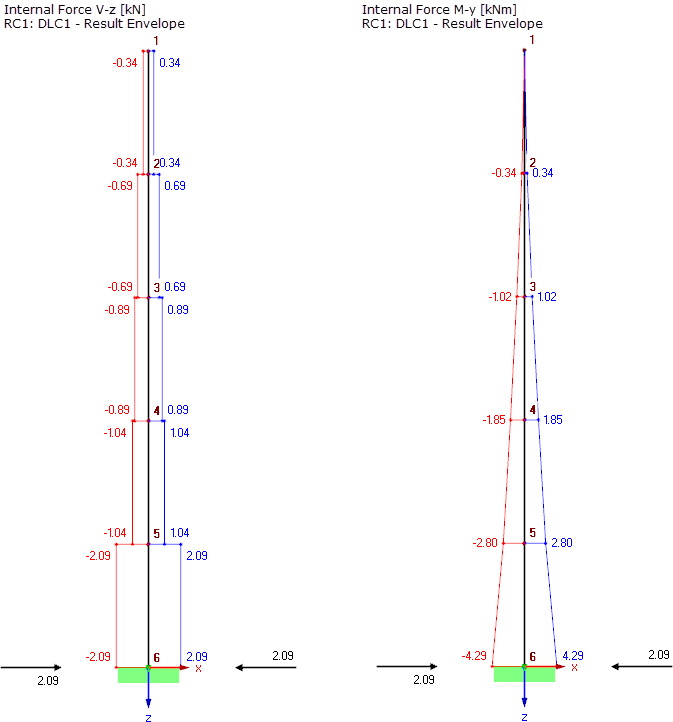
Les efforts tranchants, moments et forces d’appui résultant de ces charges équivalentes sont affichés dans la Figure 05.
Les résultats finaux de l’analyse du spectre multimodal considérant la méthode ZPA sont issus des résultats deux premières valeurs propres (ici, avec superposition modale par la règle SRSS) et des résultats des composants ZPA (voir la Figure 05).
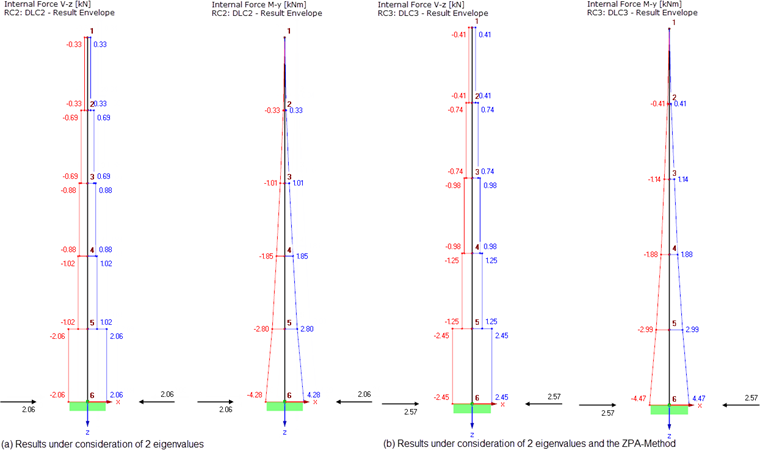
La Figure 06 compare les résultats de l’analyse du spectre de réponse en considérant les deux premières valeurs propres et les résultats finaux avec le composant ZPA. Dans la Figure 05, vous pouvez reconnaitre la somme absolue utilisée dans DYNAM Pro.
Dans la Figure 07, les résultats de l’analyse du spectre de réponse considérant toutes les cinq valeurs propres sont comparés. La méthode ZPA considère les masses aux appuis. Il en résulte une force d’appui plus importante PX = 2,57 kN. Les efforts internes sont prudents à cause de la superposition comme somme absolue (comparer la Figure 07 et la Figure 06).
Résumé
Cet exemple a permis de montrer comment la méthode ZPA est appliquée dans DYNAM Pro et que les résultats sont traçables et vérifiables. Cette méthode est utile et recommandée dans le cas où des hautes fréquences de la structure activent les composants de masse correspondants et dans le cas où des masses d’appui plus importantes existent dans la structure.
![Accélération spectrale Sa [m/s2] vs fréquence propre f [Hz] d’un spectre de réponse à bande étroite selon l’EN 1998-1 [1]](/fr/webimage/009251/2417759/01-fr-png.png)