AISC Steel Design Guide 26 – Diseño de Estructuras Resistentes a Explosiones [1] y en particular el Ejemplo 2.1 – Evaluación Preliminar de la Resistencia a Explosiones de una Estructura de Un Piso es una referencia ideal para guiar a los ingenieros mediante una aplicación simplificada de cargas de diseño por explosiones.
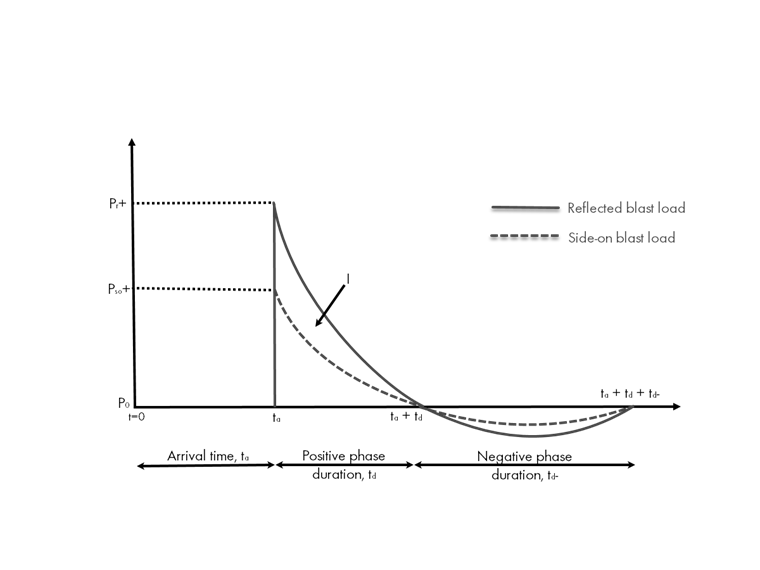
Historia Idealizada de Presión-Tiempo de Carga de Explosión
Un diagrama de historia de presión-tiempo idealizado muestra cómo varía la fuerza de presión a lo largo del tiempo después de que ocurre la explosión.
Algunos de los parámetros más importantes se enumeran directamente en el diagrama, incluidos:
- Sobrecarga máxima (Pr o Pso) … La presión instantánea que llega a la estructura por encima de la presión atmosférica ambiente.
- Duración de la fase positiva (td) … El período de tiempo para que la presión regrese a la ambiente.
- Impulso positivo (I) … La energía total de presión-tiempo aplicada durante la duración positiva calculada por el área bajo la curva.
- Duración de la fase negativa (td-) … El período de tiempo que sigue a la fase positiva donde la presión cae por debajo de la presión atmosférica.
Observe que hay dos curvas diferentes representadas en el diagrama idealizado de historia de presión-tiempo, incluidas la "carga de explosión lateral" y la "carga de explosión reflejada" indicada por la línea discontinua y la línea sólida, respectivamente. La carga de explosión lateral (también llamada carga de explosión en campo libre) incluye el subíndice "so" utilizado comúnmente en la literatura. Esto indica dónde la carga de explosión viaja paralela a una superficie, en lugar de perpendicular. Esencialmente, la carga barrerá la superficie sin objetos que la impidan. Un ejemplo de esto incluye una pared lateral paralela a una carga de explosión o una pared trasera sin exposición inmediata a la explosión.
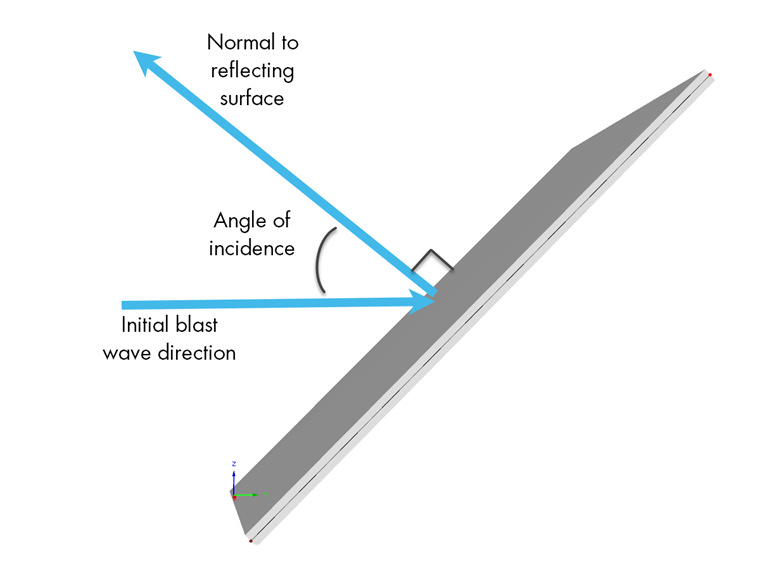
A su vez, la carga de explosión reflejada, indicada por el subíndice "r", es donde la onda de explosión golpea una superficie inclinada distinta de la paralela. Para determinar la presión reflejada, Pr, se puede utilizar la siguiente ecuación.
Pr = Cr Pso Donde Pso es la presión lateral y Cr es el coeficiente de reflexión. Cr es una función del ángulo de incidencia y la presión lateral.
La imagen a continuación demuestra cómo se puede calcular el ángulo de incidencia al considerar la dirección inicial de la onda de explosión y la onda reflejada normal a la superficie.
Una vez determinado el ángulo de incidencia, la Figura 2-193 dada en los Criterios de Instalaciones Unidas (UFC) 3-340-02 – Estructuras para Resistir los Efectos de Explosiones Accidentales [2] puede utilizarse para proporcionar el valor de Cr basado en el valor de presión máxima incidente.
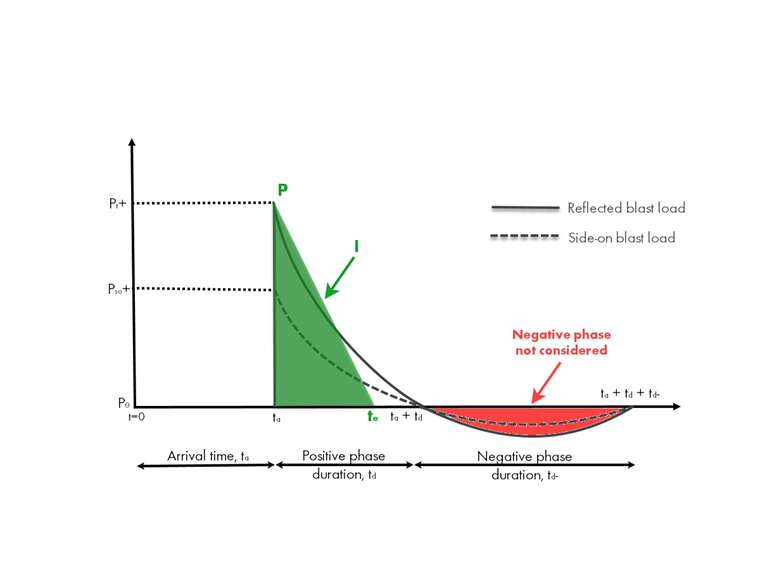
Historia Simplificada de Presión-Tiempo de Carga de Explosión
Para fines de diseño, el gráfico idealizado mostrado arriba se simplifica a una distribución triangular con un aumento instantáneo y una disminución lineal bajo la fase positiva. Para mantener la sobrecarga máxima del gráfico idealizado así como el impulso (área bajo la curva), se aproxima una duración ficticia del tiempo, te, como te = 2(I/P).
Se ha llevado a cabo una amplia investigación para determinar la relación entre el peso de la carga, la distancia de seguridad (distancia desde la estructura hasta la explosión) y los parámetros de explosión definidos en el gráfico de presión-tiempo. Manuales técnicos como el recurso [2] incluyen los parámetros de explosión de aire como una función de la distancia escalada en forma de curvas empíricas de parámetros de explosión.
La fase negativa a menudo se ignora para simplificación con estructuras simples, ya que hay poco impacto del análisis de explosiones. Sin embargo, la fase negativa se vuelve cada vez más importante cuando los elementos de la estructura son más débiles en la dirección de carga inversa o tienen un período fundamental corto con respecto a la duración de la carga.
Las variables adicionales que pueden tener influencia en el análisis de explosiones para los propósitos de este artículo no se han tomado en consideración, como las fuerzas de arrastre debidas al viento o presiones dinámicas, la protección de edificios adyacentes (reducción de carga) y la reflexión (amplificación de carga), así como cargas interiores debido a la entrada de la onda de explosión en las aberturas de la estructura.
AISC Design Guide 26 – Ejemplo 2.1 en RFEM
AISC Design Guide 26 – Ejemplo 2.1 [1] es un ejemplo ideal de referencia para aplicar el análisis de carga de explosión en RFEM, que sigue las suposiciones anteriores. La estructura de ejemplo es un edificio de acero de un piso con dimensiones de 50 ft (W) ⋅ 70 ft (L) ⋅ 15 ft (H). En la dirección corta de la estructura, se modelan marcos arriostrados en RFEM como secciones laminadas en caliente "W", mientras que en la dirección larga, se modelan marcos rígidos también con secciones "W". Las vigas y correas se modelan con secciones laminadas en caliente "C". La fachada del edificio incluye paneles de metal acanalados.
La explosión tiene un peso de carga de 500 lbs y ocurre a 50 ft de la cara frontal de la estructura, ligeramente por encima de la elevación del suelo. Con esta información, la distancia escalada, Z, se calcula según la siguiente ecuación.
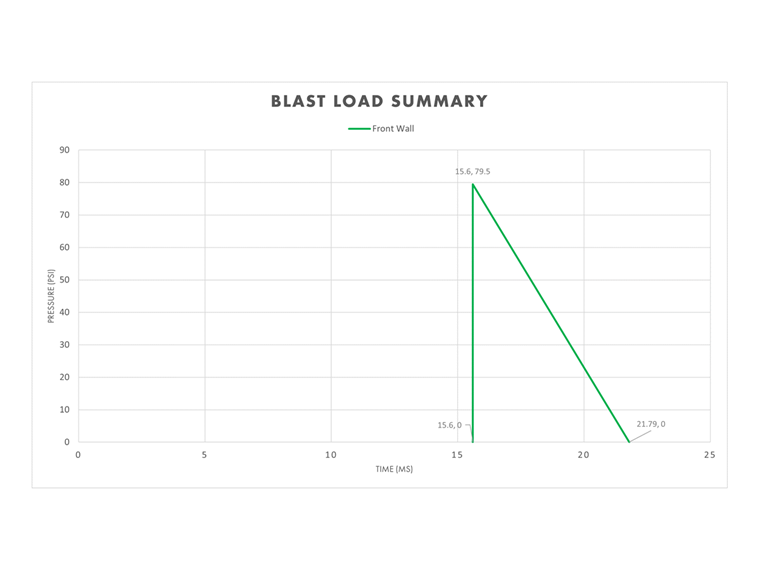
Pared Frontal
Utilizando la distancia escalada, se puede utilizar la Figura 2-15 de [2] para determinar directamente los parámetros de la onda de explosión positiva para la presión reflejada y lateral que se enumeran a continuación en la Tabla 1.
| Parámetro de Carga de Explosión | De la Figura 2-15 [2] | Valor Calculado |
|---|---|---|
| Presión máxima reflejada (+) | Pr = 79.5 psi | - |
| Presión máxima lateral (+) | Pso = 24.9 psi | - |
| Impulso reflejado (+) | Ir = 31.0W1/3 | Ir = 246 psi ms |
| Impulso lateral (+) | Iso = 12.1W1/3 | Iso = 96.0 psi ms |
| Tiempo de llegada | ta = 1.96W1/3 | ta = 15.6 ms |
| Duración de carga exponencial (+) | td = 1.77W1/3 | td = 14.0 ms |
| Velocidad de frente de choque | U = 1.75 ft/ms | - |
Dado que la pared frontal está directamente frente a la explosión inicial, las variables "reflejadas" en la Tabla 1 son aplicables a esta superficie. El enfoque triangular simplificado requiere que se calcule la duración equivalente para asegurar que el impulso (área bajo la curva) se preserve durante la fase de duración positiva.
te,r = 2Ir / Pr = 2(246 psi ms) / 29.5 psi = 6.19 ms
El gráfico inicial de presión-tiempo ahora está completo para la pared frontal.
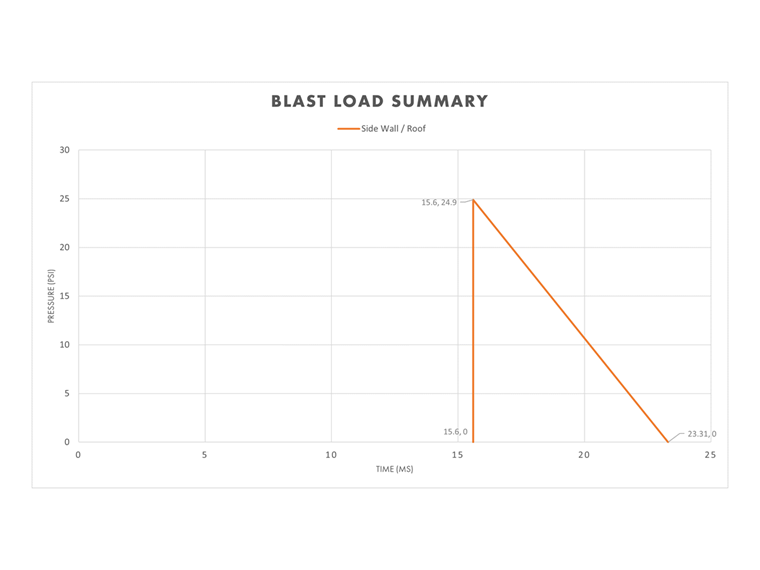
Paredes Laterales y Techo
Por simplicidad, se utiliza la distancia escalada, Z, calculada para la pared frontal para determinar las variables de explosión para las paredes laterales y el techo del edificio. Por lo tanto, los valores laterales en la Tabla 1 anterior se utilizan para definir el gráfico de presión-tiempo para esta sección del edificio. Se podría realizar un cálculo más detallado para considerar la reducción de la onda de explosión como una función de la distancia de las paredes laterales y el techo respecto a la explosión.
La duración equivalente, te, se calcula utilizando las variables laterales. te,so = 2Iso / Pso = 2(96.0 psi ms) / 24.9 psi = 7.71 ms
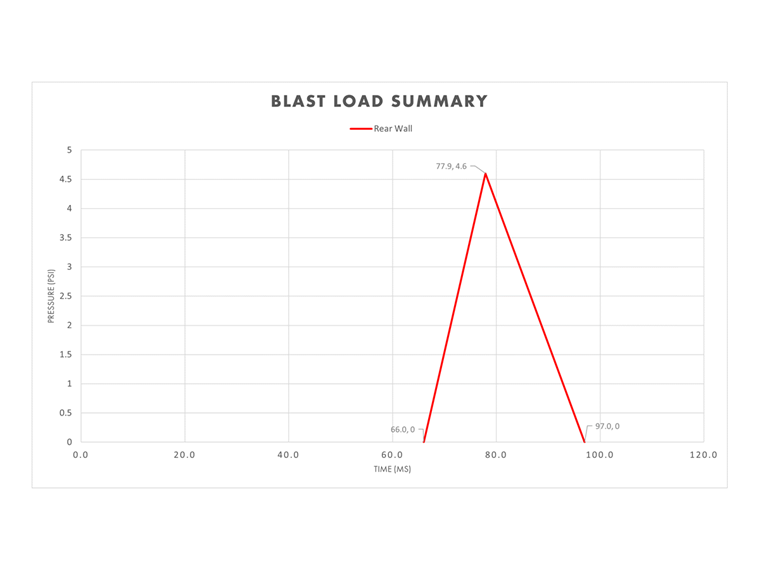
Pared Trasera
La distancia escalada, Z, para la pared trasera se modifica para considerar la longitud adicional del edificio. La distancia ahora es 50 ft + 70 ft para un total de 120 ft. Por lo tanto, Z se calcula de la siguiente manera.
|
R |
Distance from the element to charge |
|
W |
TNT equivalent charge weight |
Se puede utilizar nuevamente la Figura 2-15 de [2] para determinar los parámetros de onda de explosión positiva para la presión lateral que se enumeran a continuación en la Tabla 2.
| Parámetro de Carga de Explosión | De la Figura 2-15 [1] | Valor Calculado |
|---|---|---|
| Presión máxima lateral (+) | Pso = 4.60 psi | - |
| Impulso lateral (+) | Iso = 5.54W1/3 | Iso = 44.0 psi ms |
| Tiempo de llegada | ta = 8.32W1/3 | ta = 66.0 ms |
| Duración de carga exponencial (+) | td = 3.11W1/3 | td = 24.7 ms |
| Velocidad de frente de choque | U = 1.26 ft/ms | - |
La duración equivalente de la pared trasera, te, se puede calcular con las variables relevantes arriba.
te,so = 2Iso / Pso = 2(44.0 psi ms) / 4.60 psi = 19.1 ms
Debido a que la altura de la pared trasera es de 15 ft por encima de la elevación del suelo donde se está llevando a cabo la explosión, no ocurre un aumento instantáneo de la presión. Más bien, la velocidad de la onda de explosión, la altura de la pared trasera y el tiempo de llegada se utilizan para calcular el tiempo hasta la presión máxima, t².
t2 = L1 / U + ta = 15.0 ft / 1.26 ft/ms + 66.0 ms = 77.9 ms
El tiempo hasta el final de la carga de explosión, tf, ahora se puede determinar.
tf = t2 + te,so = 77.9 ms + 19.1 ms = 97.0 ms
Combinando todas las variables de la pared trasera calculadas arriba, el gráfico de presión-tiempo para esta sección del edificio está completo.
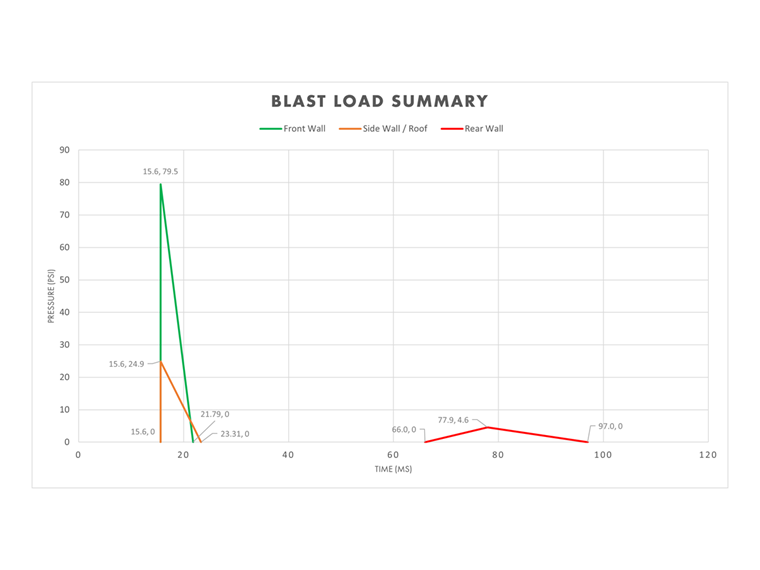
Resumen de Carga de Explosión
Las paredes frontales, laterales/techo y traseras se pueden compilar juntas para mostrar la presión total versus el tiempo e ilustrar cómo la onda de explosión impactará en las diferentes áreas de la estructura a lo largo del tiempo.
Esta información ahora se puede llevar a RFEM y a los módulos complementarios de RF-DYNAM Pro-Forced Vibrations para las definiciones de diagramas de tiempo.
Aplicación en RFEM
Ahora que los diagramas de presión-tiempo han sido definidos para las varias secciones del edificio, esta información se puede llevar al módulo complementario de RF-DYNAM Pro-Forced Vibrations en RFEM.
RF-DYNAM Pro-Natural Vibrations para determinar los períodos naturales, frecuencias y formas modales de la estructura es requerido antes de ejecutar el análisis de historia temporal. Esta parte del análisis no se discute en detalle para los propósitos de este artículo.
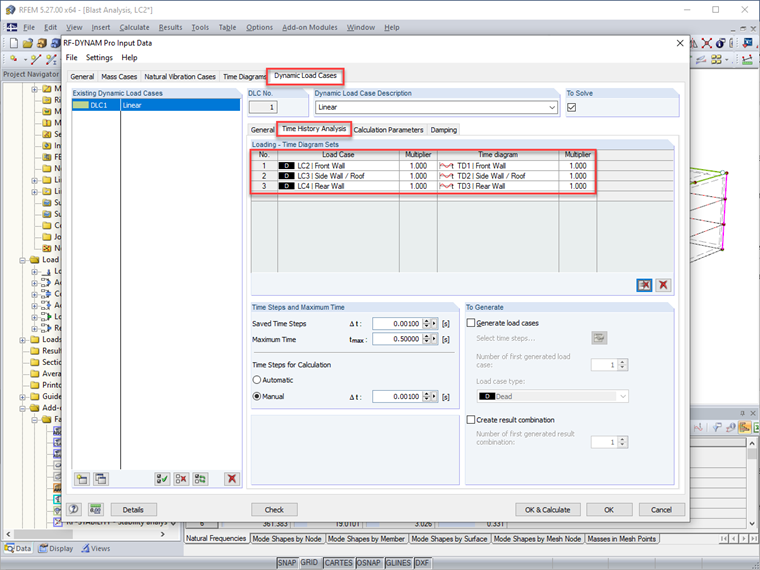
Para el análisis de historia temporal, se aplica una carga general de área como tres casos de carga separados en RFEM para emular la ubicación de carga de explosión en la estructura, incluyendo LC1 – Pared Frontal, LC2 – Pared Lateral/Techo y LC3 – Pared Trasera. Se usa una magnitud de 1 kip/ft2 solo como marcador de posición, ya que este valor dependerá luego de la función de historia temporal.
En RF-DYNAM Pro-Forced Vibrations, se definen los diagramas de tiempo para cada región de la estructura.
Observe que cada diagrama de tiempo refleja la información determinada arriba, como la presión máxima y la duración equivalente para la pared frontal, paredes laterales/techo y pared trasera.
Una vez definidos los diagramas de tiempo; las cargas generales de área en RFEM están directamente vinculadas al diagrama relevante.
Además, se deben establecer variables adicionales en el módulo complementario antes de ejecutar el análisis, como el solucionador de análisis implícito lineal de Newmark, un tiempo máximo de 0.5 segundos para la duración del análisis de historia temporal y un paso de tiempo de 0.001 segundos para ser utilizado en el cálculo. Además, utilizando la frecuencia angular de los dos modos dominantes calculados con el análisis de frecuencia natural junto con una relación de amortiguamiento de Lehr de 2%, los coeficientes de amortiguamiento de Rayleigh a y β también se establecen en el módulo.
Toda la información relevante ahora está definida para el análisis de historia temporal de explosión, y se puede ejecutar el cálculo de RFEM y RF-DYNAM Pro. Herramientas de evaluación como el monitor de curso temporal en RFEM pueden utilizarse para evaluar la respuesta y seguridad de la estructura durante la explosión. Para una demostración detallada del Ejemplo 2.1 del AISC Design Guide 26 [1] en RFEM, consulte el webinar previamente grabado Análisis de Historia Temporal de Explosiones en RFEM.