AISC Steel Design Guide 26 – Design of Blast Resistant Structures [1] (Bemessung explosionsbeständiger Konstruktionen) und insbesondere Beispiel 2.1 – Preliminary Evaluation of Blast Resistance of a One-Story Structure (vorläufige Bewertung der Explosionsbeständigkeit einer einstöckigen Konstruktion) ist eine ideale Referenz, um Ingenieure durch eine vereinfachte Lastanwendung bei der Explosionsbemessung zu führen.
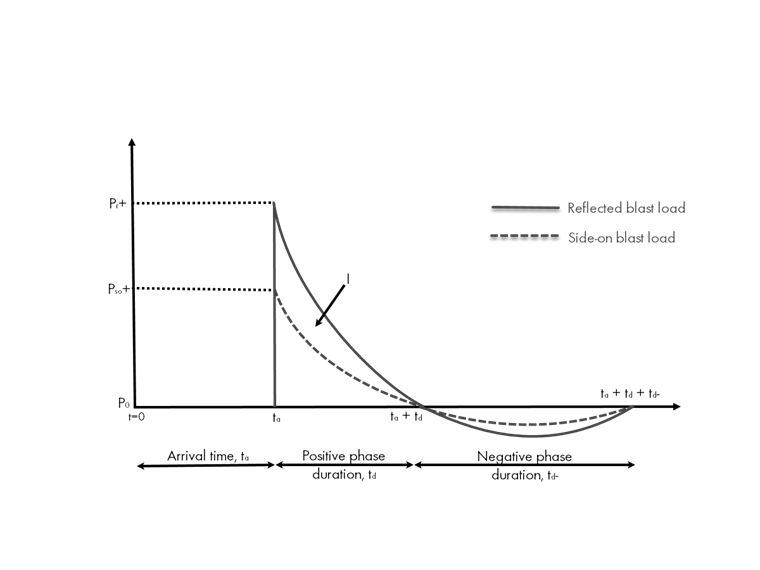
Idealisierter Verlauf von Explosionslastdruck und Zeit
Ein idealisiertes Druck-Zeit-Verlaufsdiagramm zeigt, wie sich die Druckkraft nach der Explosion im Laufe der Zeit verändert.
Einige der wichtigsten Parameter sind direkt im Diagramm aufgeführt, darunter:
- Spitzenüberdruck (Pr oder Pso) … Der momentane Druck, der über dem Umgebungsluftdruck auf die Struktur einwirkt.
- Dauer der positiven Phase (td) … Der Zeitraum, in dem der Druck wieder auf den Umgebungsdruck zurückkehrt.
- Positiver Impuls (I) … Die während der positiven Dauer aufgebrachte Gesamtdruck-Zeit-Energie, berechnet anhand der Fläche unter der Kurve.
- Dauer der negativen Phase (td-) … Der Zeitraum nach der positiven Phase, in dem der Druck unter den atmosphärischen Druck fällt.
Beachten Sie, dass im idealisierten Druck-Zeit-Verlaufsdiagramm zwei verschiedene Kurven dargestellt sind, darunter die seitliche Explosionslast und die reflektierte Explosionslast, die jeweils durch die gestrichelte bzw. die durchgezogene Linie dargestellt sind. Die seitliche Explosionslast (auch als Freifeld-Explosionslast bezeichnet) wird in der Literatur üblicherweise mit dem Index „so” gekennzeichnet. Dieser weist darauf hin, dass die Explosionslast parallel zu einer Fläche verläuft und nicht senkrecht dazu. Im Wesentlichen bedeutet dies, dass die Last ohne Hindernisse über die Fläche hinwegfegt. Beispiele hierfür sind eine zur Explosionslast parallele Seitenwand oder eine Rückwand, die nicht unmittelbar der Explosion ausgesetzt ist.
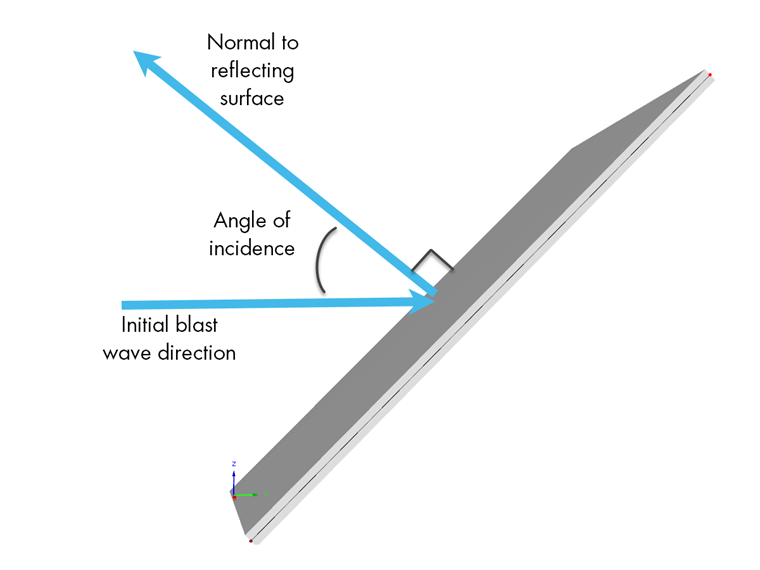
Die reflektierte Drucklast, die mit dem Index „r“ gekennzeichnet ist, entsteht hingegen, wenn die Druckwelle auf eine nicht parallele, abgewinkelte Oberfläche trifft. Zur Ermittlung des reflektierten Drucks Pr kann die folgende Gleichung verwendet werden.
Pr = Cr Pso
Dabei ist Pso der seitliche Druck und Cr der Reflexionskoeffizient. Cr ist eine Funktion des Einfallswinkels und des seitlichen Drucks.
Das Bild unten zeigt, wie der Einfallswinkel berechnet werden kann, wenn man die ursprüngliche Druckwellenrichtung und die reflektierte Wellennormale zur Fläche berücksichtigt.
Sobald der Einfallswinkel bestimmt ist, kann Abbildung 2-193 aus den United Facilities Criteria (UFC) 3-340-02 – Structures to Resist the Effects of Accidental Explosions [2] verwendet werden, um den Cr-Wert auf der Grundlage des Spitzenwerts des Einfallsüberdrucks zu ermitteln.
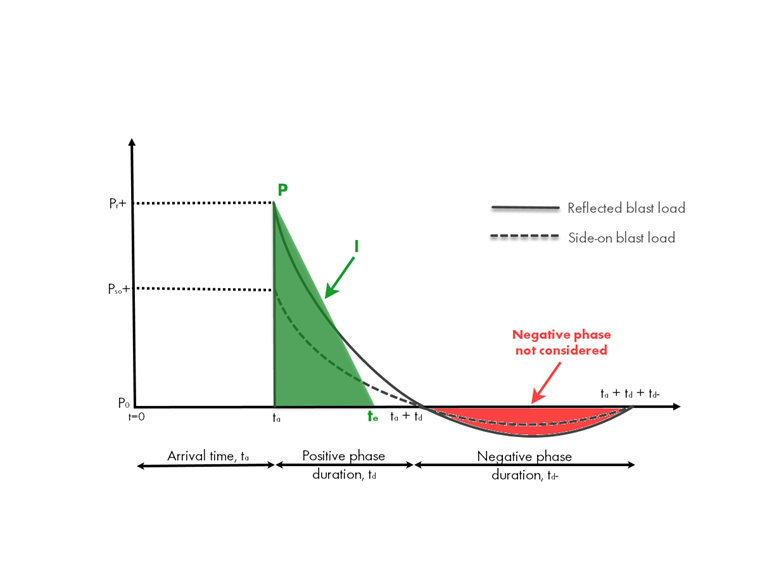
Vereinfachter Verlauf von Explosionslastdruck und Zeit
Aus Bemessungsgründen wird die oben dargestellte idealisierte Kurve zu einer dreieckigen Verteilung mit einem sofortigen Anstieg und einem linearen Abfall unter der positiven Phase vereinfacht. Um den Spitzenüberdruck aus der idealisierten Kurve sowie den Impuls (Fläche unter der Kurve) beizubehalten, wird eine fiktive Zeitdauer te als te = 2(I/P) angenähert.
Es wurden umfangreiche Untersuchungen durchgeführt, um den Zusammenhang zwischen Ladungsgewicht, Abstand (Entfernung zwischen Struktur und Explosion) und den im Druck-Zeit-Diagramm definierten Explosionsparametern zu ermitteln. Technische Handbücher wie [2] enthalten die Luftstoßparameter als Funktion des skalierten Abstands in Form von empirischen Explosionsparameterkurven.
Die negative Phase wird bei einfachen Konstruktionen zur Vereinfachung oft ignoriert, da sie nur geringe Auswirkungen auf die Explosionsanalyse hat. Die negative Phase gewinnt jedoch zunehmend an Bedeutung, wenn die Elemente der Konstruktion in umgekehrter Belastungsrichtung schwächer sind oder im Verhältnis zur Lastdauer eine kurze Grundperiode aufweisen.
Weitere Variablen, die für die Zwecke dieses Artikels einen Einfluss auf die Explosionsanalyse haben könnten, wurden nicht berücksichtigt, wie beispielsweise Widerstandskräfte aufgrund von Wind oder dynamischem Druck, Abschirmung durch benachbarte Gebäude (Lastreduzierung) und Reflexion (Lastverstärkung) sowie Innenlasten aufgrund der Explosionswelle, die in die Öffnungen des Bauwerks eindringt.
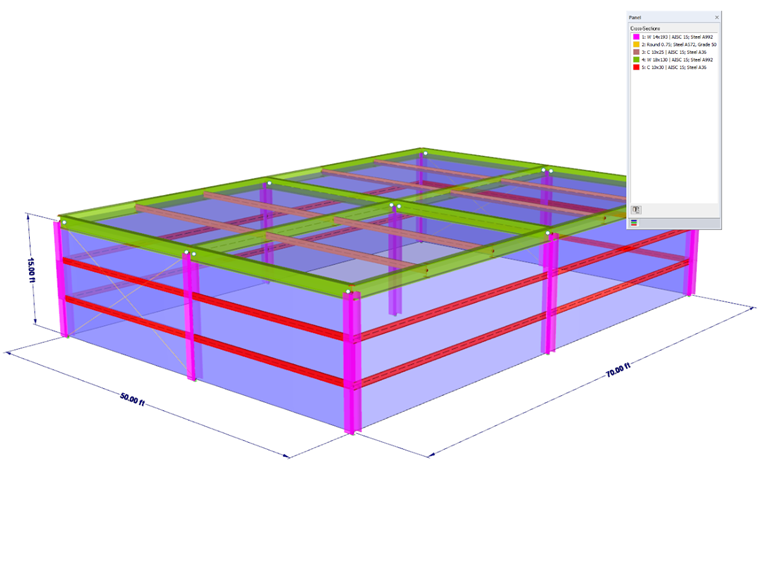
AISC Design Guide 26 – Beispiel 2.1 in RFEM
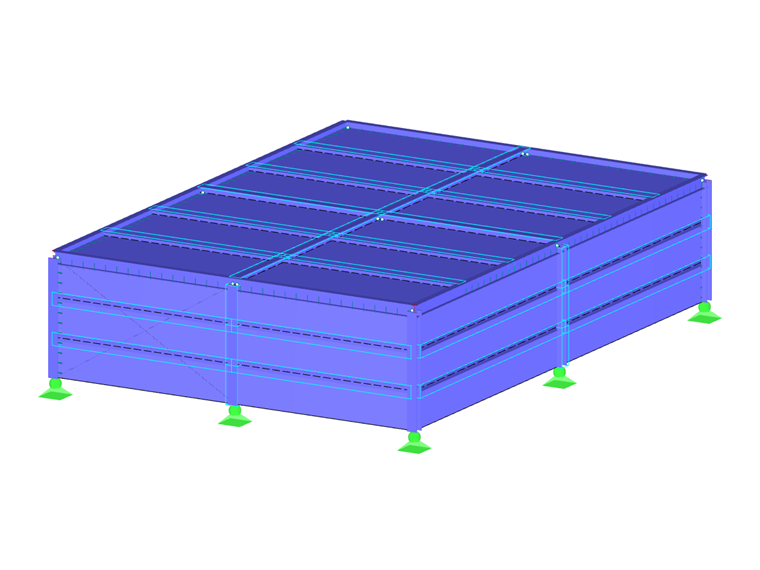
AISC Design Guide 26 – Beispiel 2.1 [1] ist ein ideales Referenzbeispiel für die Anwendung der Explosionslastanalyse in RFEM, das den oben genannten Annahmen folgt. Die Beispielkonstruktion ist ein einstöckiges Stahlgebäude mit den Abmessungen 50 ft (B) ⋅ 70 ft (L) ⋅ 15 ft (H). In der kurzen Richtung der Struktur werden in RFEM verstärkte Rahmen als warmgewalzte W-Profile modelliert, während in der langen Richtung starre Rahmen ebenfalls mit W-Profilen modelliert werden. Die Gurte und Pfetten werden mit warmgewalzten C-Profilen modelliert. Die Gebäudefassade besteht aus gerippten Metallplatten.
Die Explosion hat ein Ladungsgewicht von 500 lbs und erfolgt 50 ft von der Vorderseite der Struktur entfernt, etwas oberhalb der Bodenhöhe. Mit diesen Informationen wird dann die skalierte Entfernung Z gemäß der folgenden Gleichung berechnet.
|
R |
Distance from the element to charge |
|
W |
TNT equivalent charge weight |
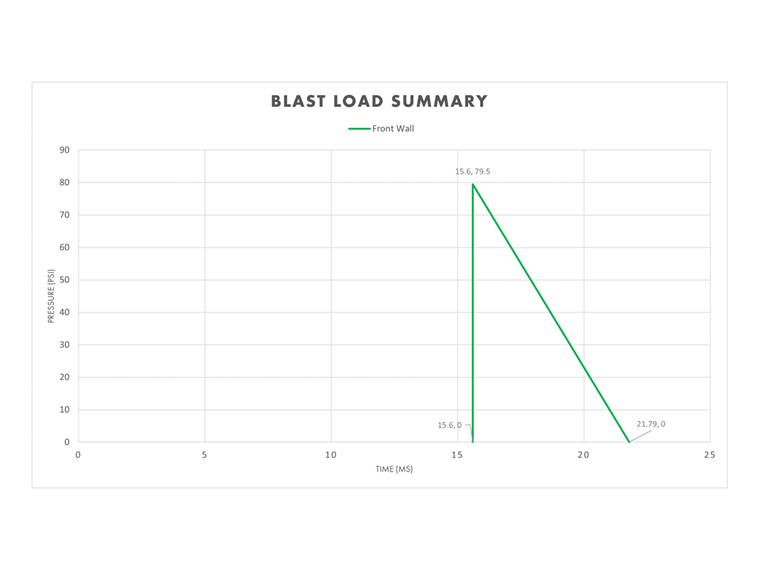
Vorderwand
Unter Verwendung der skalierten Entfernung kann Abbildung 2-15 aus [2] verwendet werden, um die positiven Druckwellenparameter für den reflektierten und seitlichen Druck, die unten in Tabelle 1 aufgeführt sind, direkt zu bestimmen.
| Explosionsbelastungsparameter | Aus Abbildung 2-15 [2] | Berechneter Wert |
|---|---|---|
| Reflektierter Spitzendruck (+) | Pr = 79.5 psi | - |
| Seitlicher Spitzendruck (+) | Pso = 24.9 psi | - |
| Reflektierter Impuls (+) | Ir = 31.0W1/3 | Ir = 246 psi ms |
| Seitlicher Impuls (+) | Iso = 12.1W1/3 | Iso = 96.0 psi ms |
| Ankunftszeit | ta = 1.96W1/3 | ta = 15.6 ms |
| Exponentielle Lastdauer (+) | td = 1.77W1/3 | td = 14.0 ms |
| Schockfrontgeschwindigkeit | U = 1.75 ft/ms | - |
Da die Vorderwand direkt der ursprünglichen Explosion ausgesetzt ist, gelten die „reflektierten” Variablen in Tabelle 1 für diese Oberfläche. Der vereinfachte dreieckige Ansatz erfordert die Berechnung der äquivalenten Dauer, um sicherzustellen, dass der Impuls (Fläche unter der Kurve) über die Dauer der positiven Phase erhalten bleibt.
te,r = 2Ir / Pr = 2(246 psi ms) / 29.5 psi = 6.19 ms
Die anfängliche Druck-Zeit-Kurve für die Vorderwand ist nun vollständig.
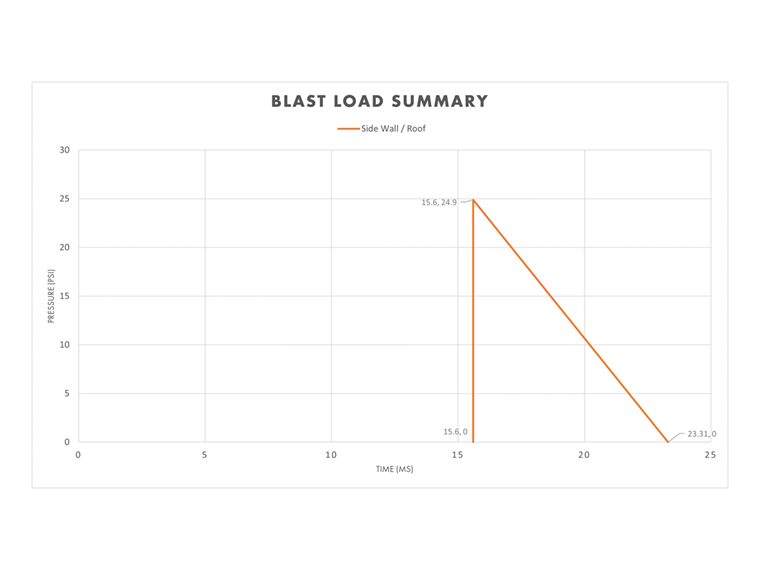
Seitenwände und Dach
Der Einfachheit halber wird der für die Vorderwand berechnete skalierte Abstand Z verwendet, um die Explosionsvariablen für die Seitenwände und das Dach des Gebäudes zu bestimmen. Daher werden die Werte für die Seitenwände in Tabelle 1 oben verwendet, um das Druck-Zeit-Diagramm für diesen Teil des Gebäudes zu definieren. Eine detailliertere Berechnung könnte durchgeführt werden, um die Reduzierung der Explosionswelle als Funktion des Abstands der Seitenwände und des Daches von der Explosion zu berücksichtigen.
Die äquivalente Dauer te wird anhand der seitlichen Variablen berechnet.
te,so = 2Iso / Pso = 2(96.0 psi ms) / 24.9 psi = 7.71 ms
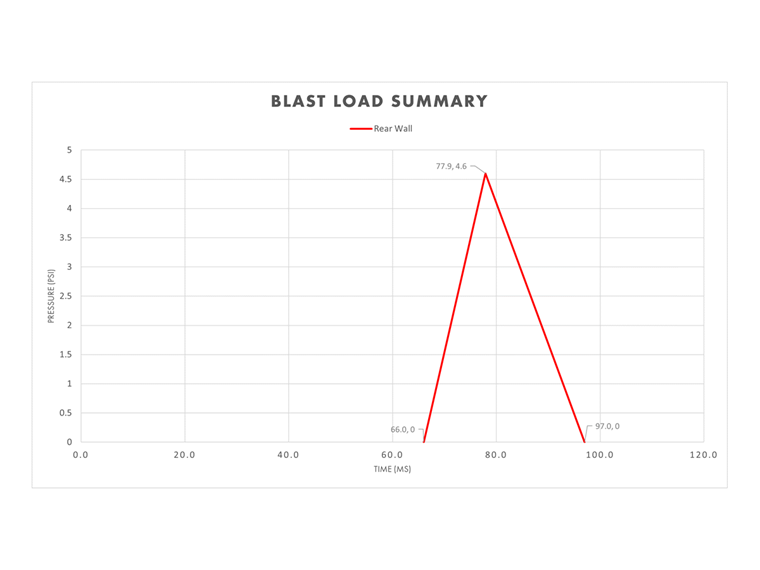
Rückwand
Der skalierte Abstand Z für die Rückwand wird angepasst, um die zusätzliche Länge des Gebäudes zu berücksichtigen. Der Abstand beträgt nun 50 ft + 70 ft, also insgesamt 120 ft. Daher wird Z wie folgt berechnet.
|
R |
Distance from the element to charge |
|
W |
TNT equivalent charge weight |
Abbildung 2-15 aus [2] kann erneut verwendet werden, um die positiven Druckwellenparameter für den seitlichen Druck zu bestimmen, siehe Tabelle 2 unten.
| Explosionsbelastungsparameter | Aus Abbildung 2-15 [1] | Berechneter Wert |
|---|---|---|
| Seitlicher Spitzendruck (+) | Pso = 4.60 psi | - |
| Seitlicher Impuls (+) | Iso = 5.54W1/3 | Iso = 44.0 psi ms |
| Ankunftszeit | ta = 8.32W1/3 | ta = 66.0 ms |
| Exponentielle Lastdauer (+) | td = 3.11W1/3 | td = 24.7 ms |
| Schockfrontgeschwindigkeit | U = 1.26 ft/ms | - |
Die äquivalente Dauer der Rückwand, te, kann mit den oben genannten relevanten Variablen berechnet werden.
te,so = 2Iso / Pso = 2(44.0 psi ms) / 4.60 psi = 19.1 ms
Da die Höhe der Rückwand 15 Fuß über der Bodenhöhe liegt, wo die Explosion stattfindet, kommt es nicht zu einem sofortigen Druckanstieg. Vielmehr werden die Geschwindigkeit der Druckwelle, die Höhe der Rückwand und die Ankunftszeit verwendet, um die Zeit bis zum Erreichen des Spitzendrucks, t², zu berechnen.
t2 = L1 / U + ta = 15.0 ft / 1.26 ft/ms + 66.0 ms = 77.9 ms
Die Zeit bis zum Ende der Explosionslast, tf, kann nun bestimmt werden.
tf = t2 + te,so = 77.9 ms + 19.1 ms = 97.0 ms
Durch Kombination aller oben berechneten Variablen für die Rückwand ist die Druck-Zeit-Kurve für diesen Abschnitt des Gebäudes vollständig.
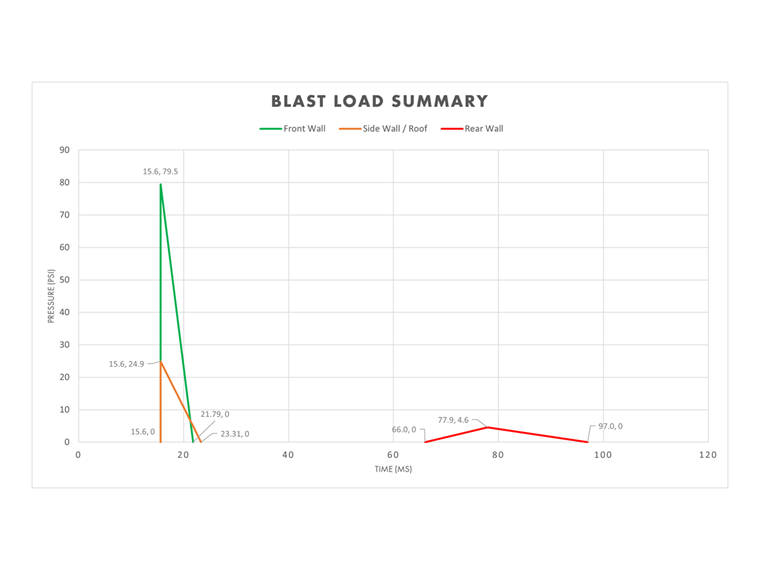
Zusammenfassung der Explosionslast
Die Vorder-, Seiten-/Dach- und Rückwände können zusammengeführt werden, um den Gesamtdruck über die Zeit darzustellen und zu veranschaulichen, wie sich die Druckwelle im Laufe der Zeit auf die verschiedenen Bereiche der Struktur auswirkt.
Diese Informationen können nun in RFEM und das Zusatzmodul RF-DYNAM Pro - Erzwungene Schwingungen für die Zeitdiagrammdefinitionen übernommen werden.
Anwendung in RFEM
Nachdem die Druck-Zeit-Diagramme für die verschiedenen Abschnitte des Gebäudes definiert wurden, können diese Informationen in das Zusatzmodul RF-DYNAM Pro - Erzwungene Schwingungen in RFEM übernommen werden.
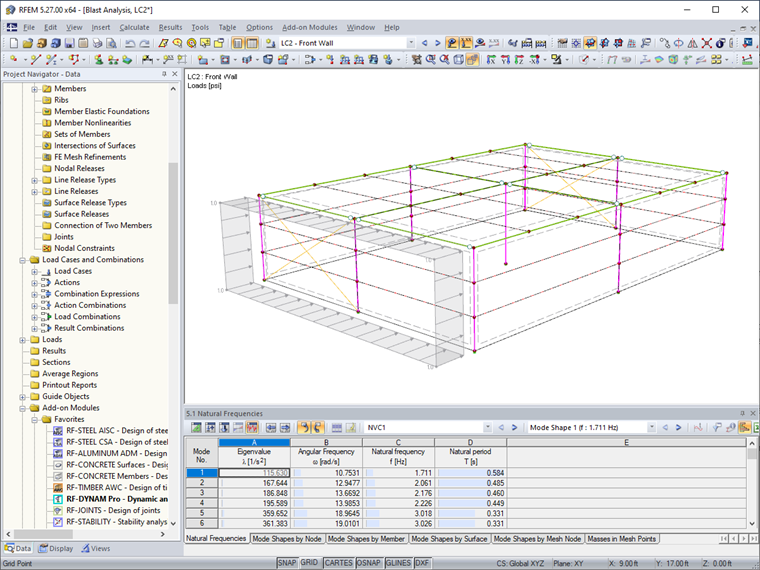
RF-DYNAM Pro - Erzwungene Schwingungen wird zur Ermittlung der Eigenperioden, Eigenfrequenzen und Eigenformen der Konstruktion verwendet und ist vor der Durchführung der Zeitverlaufsanalyse erforderlich. Dieser Teil der Analyse wird im Rahmen dieses Artikels nicht näher erläutert.
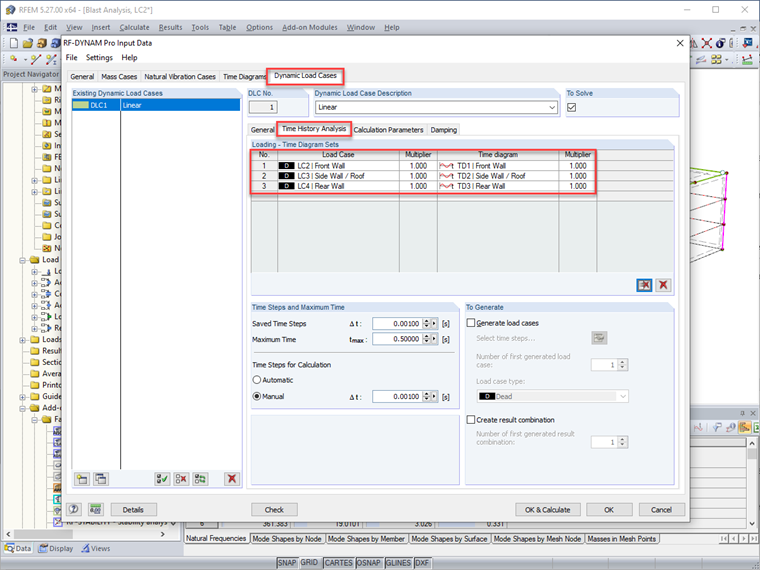
Für die Zeitverlaufsanalyse wird in RFEM eine allgemeine Flächenlast als drei separate Lastfälle angewendet, um die Lage der Explosionslast auf der Struktur zu simulieren, darunter LF1 – Vorderwand, LF2 – Seitenwand/Dach und LF3 – Rückwand. Eine Größe von 1 kip/ft2 wird nur als Platzhalter verwendet, da dieser Wert später von der Zeitverlaufsfunktion abhängt.
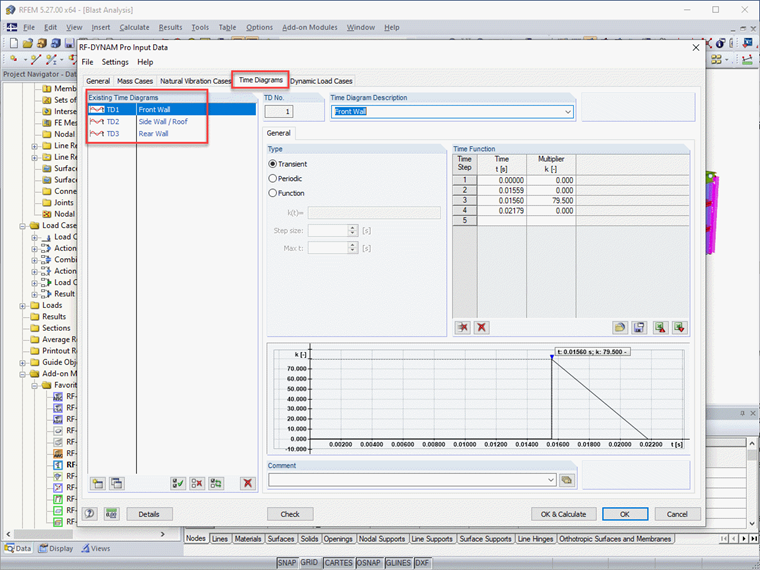
In RF-DYNAM Pro - Erzwungene Schwingungen werden die Zeitdiagramme für jeden Bereich der Struktur definiert.
Beachten Sie, dass jedes Zeitdiagramm die oben ermittelten Informationen widerspiegelt, wie z.B. den Spitzendruck und die äquivalente Dauer für die Vorderwand, die Seitenwände/das Dach und die Rückwand.
Sobald die Zeitdiagramme definiert sind, werden die allgemeinen Flächenlasten in RFEM direkt mit dem entsprechenden Diagramm verknüpft.
Vor der Durchführung der Analyse müssen im Zusatzmodul weitere Variablen festgelegt werden, wie beispielsweise der lineare implizite Newmark-Analyse-Löser, eine maximale Dauer von 0,5 Sekunden für die Zeitverlaufsanalyse und ein Zeitschritt von 0,001 Sekunden für die Berechnung. Darüber hinaus werden unter Verwendung der Winkelfrequenz aus den beiden dominanten Formen, die mit der Eigenfrequenzanalyse berechnet wurden, zusammen mit einem Lehr'schen Dämpfungsverhältnis von 2 % auch die Rayleigh-Dämpfungskoeffizienten a und β im Modul eingestellt.
Alle wesentlichen Informationen für die Zeitverlaufsanalyse der Explosion sind nun definiert und die Berechnung mit RFEM und RF-DYNAM Pro kann durchgeführt werden. Mit Hilfe von Auswertungstools wie dem Zeitverlaufsmonitor in RFEM können Sie die Reaktion und Sicherheit der Struktur im Verlauf der Explosion beurteilen. Eine detaillierte Demonstration des AISC Design Guide 26 Beispiel 2.1 [1] in RFEM finden Sie im zuvor aufgezeichneten Webinar „Zeitverlaufsanalyse einer Explosion in RFEM”.