Guia de design de aço AISC 26 – Projeto de Estruturas Resistentes a Explosões [1] e em particular Exemplo 2.1 – Avaliação Preliminar da Resistência a Explosões de uma Estrutura de Um Andar é uma referência ideal para orientar engenheiros através de uma aplicação simplificada de carga de explosão.
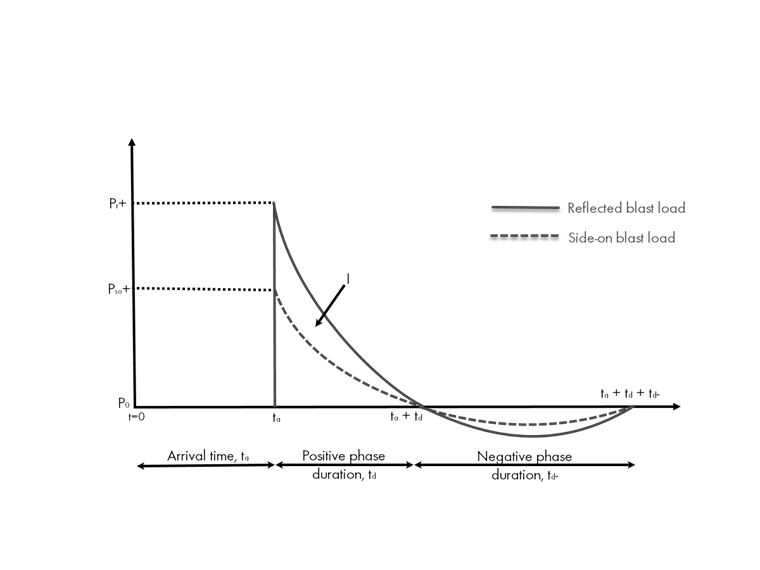
História Idealizada de Pressão-Tempo de Carga de Explosão
Um diagrama idealizado de história de pressão-tempo mostra como a força de pressão varia ao longo do tempo após a explosão ocorrer.
Alguns dos parâmetros mais importantes estão listados diretamente no diagrama, incluindo:
- Sobreatensão de pico (Pr ou Pso) … A pressão instantânea que chega à estrutura acima da pressão atmosférica ambiente.
- Duração da fase positiva (td) … O período de tempo para a pressão retornar ao ambiente.
- Impulso positivo (I) … A energia total de pressão-tempo aplicada durante a duração positiva calculada pela área sob a curva.
- Duração da fase negativa (td-) … O período de tempo após a fase positiva onde a pressão cai abaixo da pressão atmosférica.
Note que há duas curvas diferentes representadas no diagrama idealizado de pressão-tempo, incluindo a "carga lateral da explosão" e a "carga refletida da explosão" indicadas pela linha tracejada e a linha sólida, respectivamente. A carga lateral da explosão (também chamada de carga de explosão em campo livre) inclui o subscrito "so" usado comumente na literatura. Isso indica onde a carga de explosão viaja paralela a uma superfície, em vez de perpendicular. Essencialmente, a carga varrerá a superfície sem objetos que a impeçam. Um exemplo disso inclui uma parede lateral paralela a uma carga de explosão ou uma parede traseira sem exposição imediata à explosão.
Por sua vez, a carga refletida da explosão, indicada pelo subscrito "r", é onde a onda de explosão atinge uma superfície inclinada que não é paralela. Para determinar a pressão refletida, Pr, a seguinte equação pode ser usada.
Pr = Cr Pso Onde Pso é a pressão lateral e Cr é o coeficiente de reflexão. Cr é uma função do ângulo de incidência e da pressão lateral.
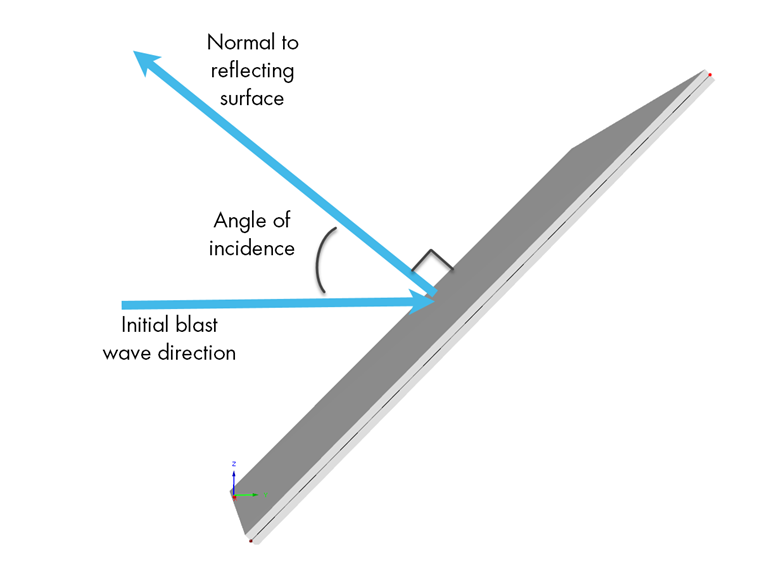
A imagem abaixo demonstra como o ângulo de incidência pode ser calculado ao considerar a direção inicial da onda de explosão e a onda refletida normal à superfície.
Uma vez determinado o ângulo de incidência, a Figura 2-193 dada nos Critérios de Instalações Unidas (UFC) 3-340-02 – Estruturas para Resistir aos Efeitos de Explosões Acidentais [2] pode ser usada para fornecer o valor de Cr com base no valor de Sobreatensão Incidente de Pico.
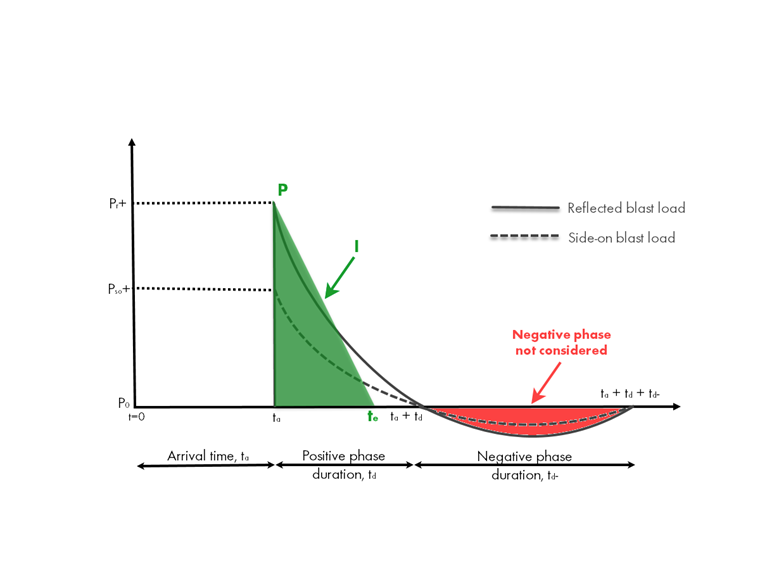
História Simplificada de Pressão-Tempo de Carga de Explosão
Para fins de design, o gráfico idealizado mostrado acima é simplificado para uma distribuição triangular com um aumento instantâneo e decaimento linear sob a fase positiva. Para manter a sobreatensão de pico do gráfico idealizado, bem como o impulso (área sob a curva), uma duração de tempo fictícia, te, é aproximada como te = 2(I/P).
Extensas pesquisas para determinar o relacionamento entre o peso da carga, a distância de afastamento (distância da estrutura até a explosão) e os parâmetros de explosão definidos no gráfico de pressão-tempo foram realizadas. Manuais técnicos como o recurso [2] incluem os parâmetros de explosão aérea como uma função da distância escalonada na forma de curvas empíricas de parâmetros de explosão.
A fase negativa é frequentemente ignorada para simplificação com estruturas simples, pois há pouco impacto da análise de explosão. No entanto, a fase negativa torna-se cada vez mais importante quando os elementos da estrutura são mais fracos na direção de carregamento reverso ou têm um período fundamental curto em relação à duração da carga.
Variáveis adicionais que podem ter influência na análise de explosão para fins deste artigo não foram consideradas, tais como forças de arrasto devido ao vento ou pressões dinâmicas, proteção de edifícios adjacentes (redução de carga) e reflexão (amplificação de carga), e cargas internas devido à entrada da onda de explosão pelas aberturas da estrutura.
Guia de Design da AISC 26 – Exemplo 2.1 no RFEM
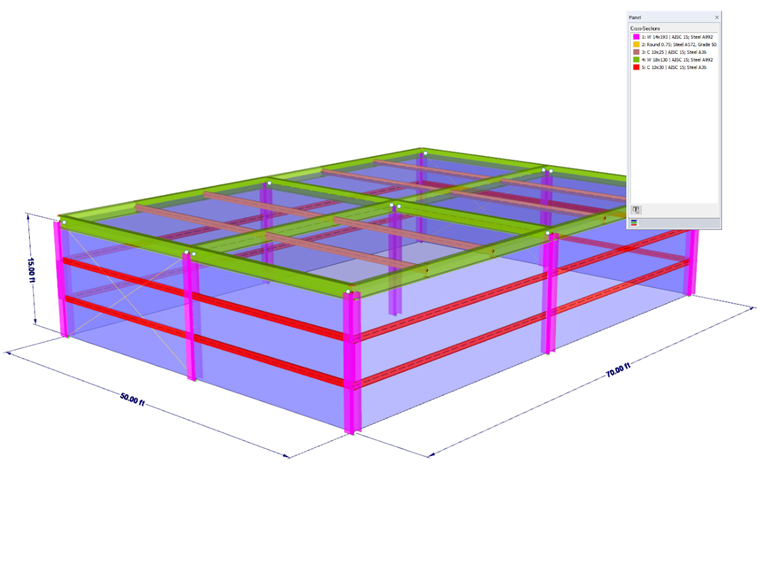
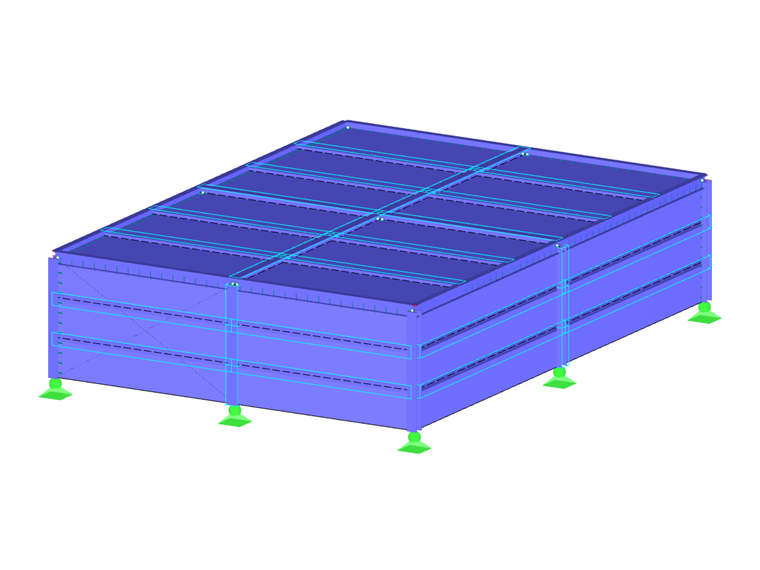
O Guia de Design da AISC 26 – Exemplo 2.1 [1] é um exemplo de referência ideal para aplicar a análise de carga de explosão no RFEM que segue as suposições acima. A estrutura do exemplo é um edifício de aço de um andar com dimensões de 50 pés (L) ⋅ 70 pés (C) ⋅ 15 pés (A). Na direção curta da estrutura, quadros escorados são modelados no RFEM como seções W laminadas a quente, enquanto na direção longa, quadros rígidos também são modelados com seções W. Os metais e purlins são modelados com seções C laminadas a quente. A fachada do edifício inclui painéis de metal com nervuras.
A explosão tem um peso de carga de 500 libras e ocorre a 50 pés da face frontal da estrutura um pouco acima do nível do solo. Com estas informações, a distância escalonada, Z, é então calculada de acordo com a seguinte equação.
|
R |
Distance from the element to charge |
|
W |
TNT equivalent charge weight |
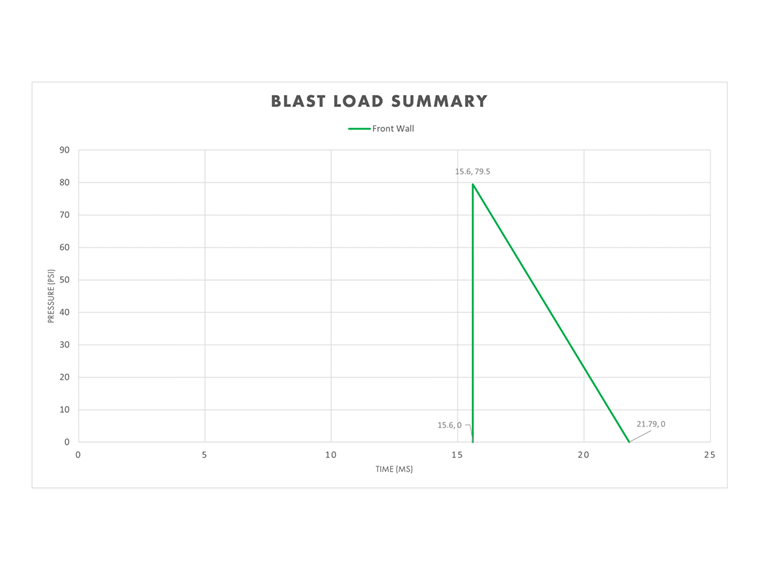
Parede Frontal
Usando a distância escalonada, a Figura 2-15 de [2] pode ser utilizada para determinar diretamente os parâmetros da onda de explosão positiva para a pressão refletida e lateral listada abaixo na Tabela 1.
| Parâmetro de Carga de Explosão | Da Figura 2-15 [2] | Valor Calculado |
|---|---|---|
| Pressão de pico refletida (+) | Pr = 79.5 psi | - |
| Pressão de pico lateral (+) | Pso = 24.9 psi | - |
| Impulso refletido (+) | Ir = 31.0W1/3 | Ir = 246 psi ms |
| Impulso lateral (+) | Iso = 12.1W1/3 | Iso = 96.0 psi ms |
| Tempo de chegada | ta = 1.96W1/3 | ta = 15.6 ms |
| Duração da carga exponencial (+) | td = 1.77W1/3 | td = 14.0 ms |
| Velocidade da frente de choque | U = 1.75 ft/ms | - |
Como a parede frontal está diretamente de frente para a explosão inicial, as variáveis "refletidas" na Tabela 1 são aplicáveis a esta superfície. A abordagem triangular simplificada requer que a duração equivalente seja calculada para garantir que o impulso (área sob a curva) seja preservado durante a fase de duração positiva.
te,r = 2Ir / Pr = 2(246 psi ms) / 29.5 psi = 6.19 ms
O gráfico inicial de pressão-tempo agora está completo para a parede frontal.
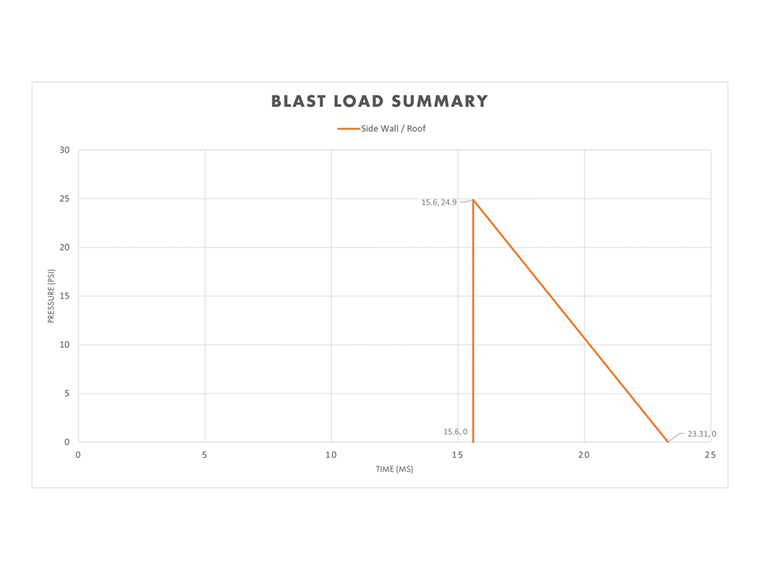
Paredes Laterais e Teto
Para simplificar, a distância escalonada, Z, calculada para a parede frontal é usada para determinar as variáveis de explosão para as paredes laterais e o teto da construção. Portanto, os valores laterais na Tabela 1 acima são usados para definir o gráfico de pressão-tempo para esta seção do edifício. Um cálculo mais detalhado poderia ser realizado para considerar a redução da onda de explosão como uma função da distância da parede lateral e do teto em relação à explosão.
A duração equivalente, te, é calculada usando as variáveis laterais. te,so = 2Iso / Pso = 2(96.0 psi ms) / 24.9 psi = 7.71 ms
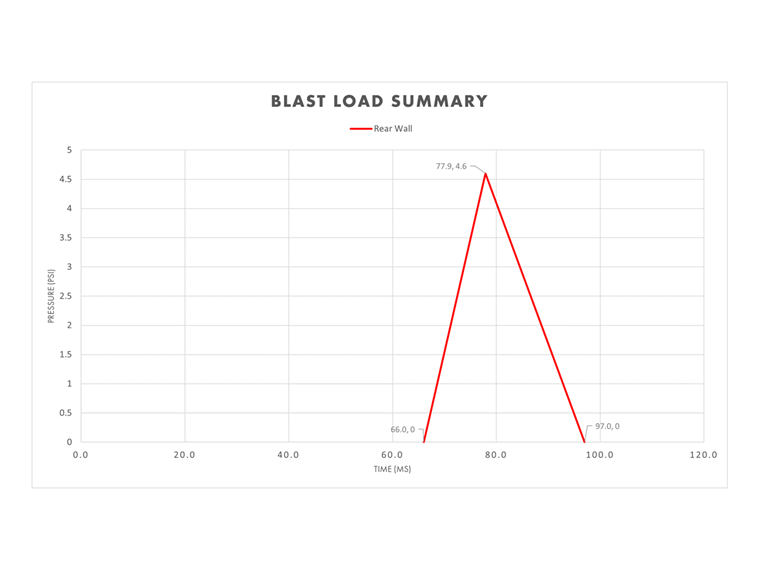
Parede Traseira
A distância escalonada, Z, para a parede traseira é modificada para considerar o comprimento adicional do edifício. A distância agora é de 50 pés + 70 pés para um total de 120 pés. Portanto, Z é calculado como segue.
|
R |
Distance from the element to charge |
|
W |
TNT equivalent charge weight |
A Figura 2-15 de [2] pode ser utilizada novamente para determinar os parâmetros da onda de explosão positiva para a pressão lateral listada abaixo na Tabela 2.
| Parâmetro de Carga de Explosão | Da Figura 2-15 [1] | Valor Calculado |
|---|---|---|
| Pressão de pico lateral (+) | Pso = 4.60 psi | - |
| Impulso lateral (+) | Iso = 5.54W1/3 | Iso = 44.0 psi ms |
| Tempo de chegada | ta = 8.32W1/3 | ta = 66.0 ms |
| Duração da carga exponencial (+) | td = 3.11W1/3 | td = 24.7 ms |
| Velocidade da frente de choque | U = 1.26 ft/ms | - |
A duração equivalente da parede traseira, te, pode ser calculada com as variáveis relevantes acima.
te,so = 2Iso / Pso = 2(44.0 psi ms) / 4.60 psi = 19.1 ms
Como a altura da parede traseira é de 15 pés acima do nível do solo onde a explosão está ocorrendo, não ocorre um aumento instantâneo na pressão. Pelo contrário, a velocidade da onda de explosão, a altura da parede traseira e o tempo de chegada são usados para calcular o tempo até a pressão de pico, t².
t2 = L1 / U + ta = 15.0 ft / 1.26 ft/ms + 66.0 ms = 77.9 ms
O tempo até o final da carga de explosão, tf, pode agora ser determinado.
tf = t2 + te,so = 77.9 ms + 19.1 ms = 97.0 ms
Combinando todas as variáveis da parede traseira calculadas acima, o gráfico de pressão-tempo para esta seção do edifício está completo.
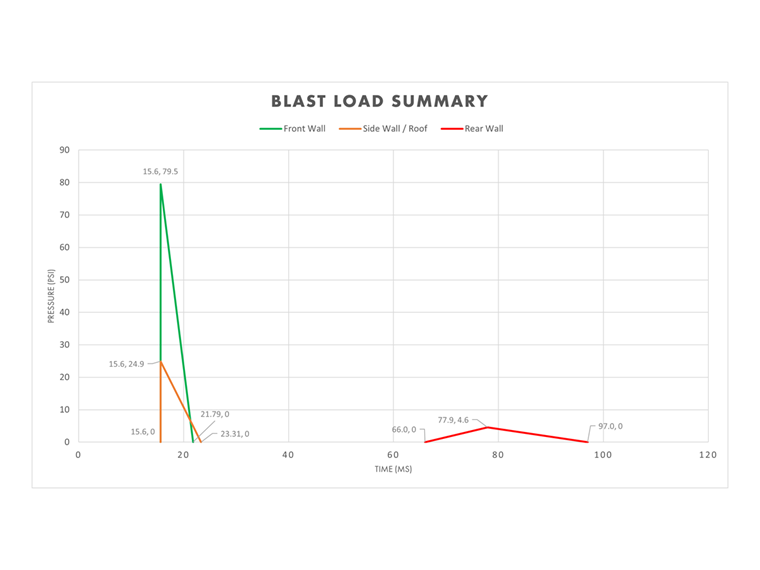
Resumo da Carga de Explosão
As paredes frontal, laterais/teto e traseira podem ser compiladas juntas para exibir a pressão total versus o tempo e ilustrar como a onda de explosão impactará as diferentes áreas da estrutura ao longo do tempo.
Esta informação pode agora ser levada para o RFEM e os módulos de complementos RF-DYNAM Pro-Forced Vibrations para as definições do diagrama temporal.
Aplicação no RFEM
Agora que os diagramas de pressão-tempo foram definidos para as várias seções do edifício, esta informação pode ser levada para o módulo de complemento RF-DYNAM Pro-Forced Vibrations no RFEM.
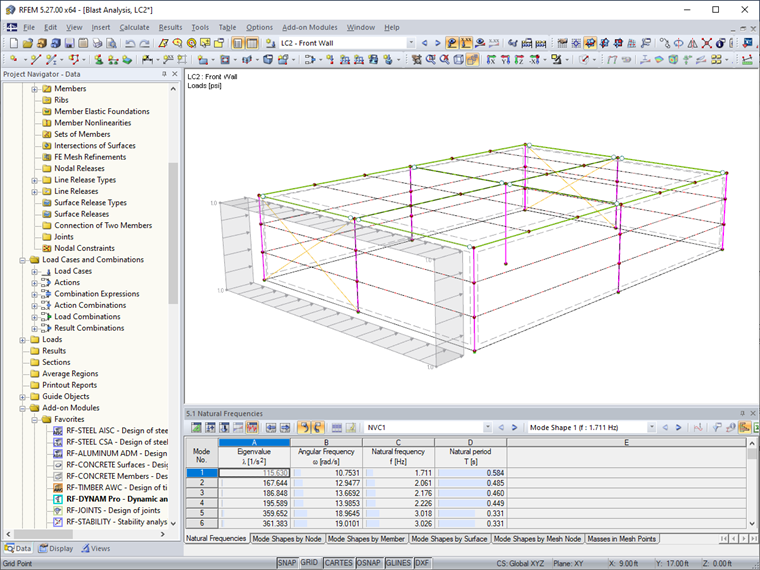
RF-DYNAM Pro-Natural Vibrations para determinar os períodos naturais da estrutura, frequências e formas modais é necessário antes de executar a análise histórica temporal. Esta parte da análise não é discutida em detalhe para fins deste artigo.
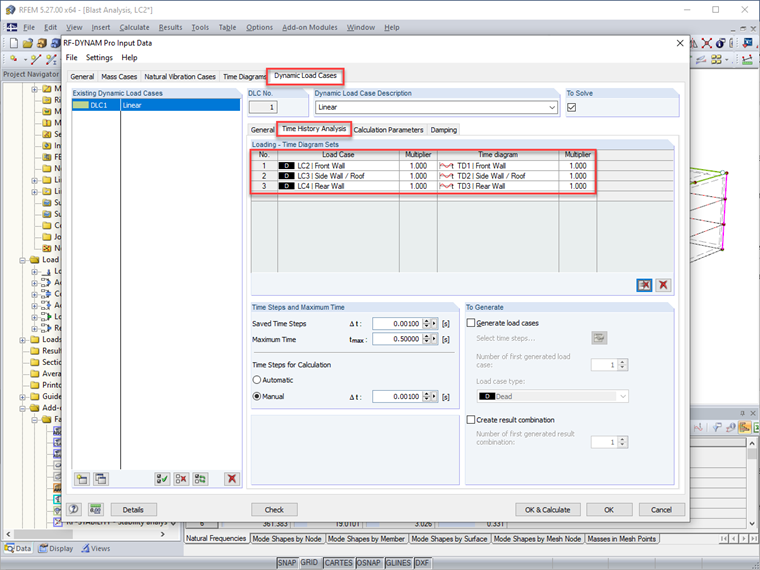
Para a análise histórica temporal, uma carga geral de área é aplicada como três casos de carga separados no RFEM para emular a localização da carga de explosão na estrutura, incluindo LC1 – Parede Frontal, LC2 – Parede Lateral/Teto, e LC3 – Parede Traseira. Uma magnitude de 1 kip/ft2 é usada apenas como um valor de referência, já que este valor será mais tarde dependente da função histórica temporal.
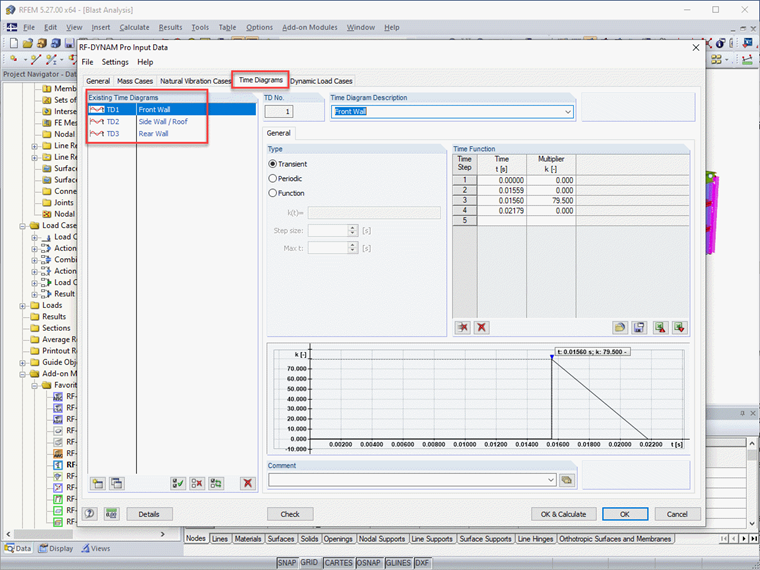
No módulo RF-DYNAM Pro-Forced Vibrations, os diagramas temporais são definidos para cada região da estrutura.
Note que cada diagrama temporal reflete a informação determinada acima, tal como a pressão de pico e a duração equivalente para a parede frontal, paredes laterais/teto, e parede traseira.
Uma vez definidos os diagramas temporais, as cargas gerais de área no RFEM são diretamente vinculadas ao diagrama relevante.
Variáveis adicionais também devem ser definidas no módulo de complemento antes de executar a análise, tais como o solver de análise implícito linear de Newmark, um tempo máximo de 0,5 segundos para a duração da análise histórica temporal, e um passo de tempo de 0,001 segundos para ser usado no cálculo. Além disso, utilizando a frequência angular dos dois modos dominantes calculados com a análise de frequência natural junto com uma razão de amortecimento de Lehr de 2%, os coeficientes de amortecimento de Rayleigh, a e β, também são definidos no módulo.
Todas as informações relevantes agora estão definidas para a análise histórica temporal de explosão, e o cálculo do RFEM e RF-DYNAM Pro pode ser executado. Ferramentas de avaliação, como o monitor de curso temporal no RFEM, podem ser usadas para avaliar a resposta e segurança da estrutura ao longo do curso da explosão. Para uma demonstração detalhada do Exemplo 2.1 do Guia de Design da AISC 26 [1] no RFEM, consulte o webinar previamente gravado Análise de Histórico Temporal de Explosão no RFEM.