Guida alla progettazione dell'acciaio AISC 26 – Progettazione di strutture resistenti alle esplosioni [1] e in particolare l'Esempio 2.1 – Valutazione preliminare della resistenza alle esplosioni di una struttura a un piano è un riferimento ideale per guidare gli ingegneri attraverso un'applicazione semplificata del carico di progettazione per esplosioni.
Storia ideale della pressione-tempo del carico d'esplosione
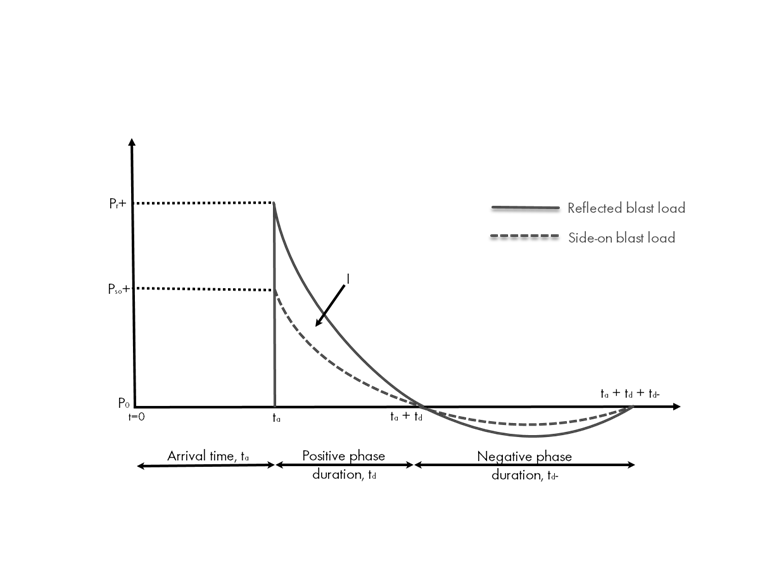
Un diagramma idealizzato della storia della pressione-tempo mostra come la forza di pressione varia nel tempo dopo che è avvenuta l'esplosione.
Alcuni dei parametri più importanti sono elencati direttamente nel diagramma, tra cui:
- Sovrapressione di picco (Pr o Pso) … La pressione istantanea che arriva alla struttura al di sopra della pressione atmosferica ambiente.
- Durata della fase positiva (td) … Il periodo di tempo per cui la pressione torna al livello ambiente.
- Impulso positivo (I) … L'energia totale pressione-tempo applicata durante la durata positiva calcolata tramite l'area sotto la curva.
- Durata della fase negativa (td-) … Il periodo di tempo seguente alla fase positiva in cui la pressione scende al di sotto della pressione atmosferica.
Si noti che ci sono due diverse curve rappresentate nel diagramma della storia ideale della pressione-tempo, inclusi il "carico laterale dell'esplosione" e il "carico riflesso dell'esplosione" indicati rispettivamente dalla linea tratteggiata e dalla linea continua. Il carico laterale dell'esplosione (noto anche come carico dell'esplosione in campo libero) include il pedice "so" comunemente usato nella letteratura. Questo indica dove il carico dell'esplosione viaggia parallelo a una superficie, piuttosto che perpendicolare. Essentially, il carico si sposterà sulla superficie senza ostacoli. Un esempio di questo include un muro laterale parallelo a un carico di esplosione o un muro posteriore senza esposizione immediata all'esplosione.
A sua volta, il carico riflesso dell'esplosione, indicato dal pedice "r", è dove l'onda esplosiva colpisce una superficie angolata diversa dalla direzione parallela. Per determinare la pressione riflessa, Pr, si può utilizzare la seguente equazione.
Pr = Cr Pso Dove Pso è la pressione laterale e Cr è il coefficiente di riflessione. Cr è una funzione dell'angolo di incidenza e della pressione laterale.
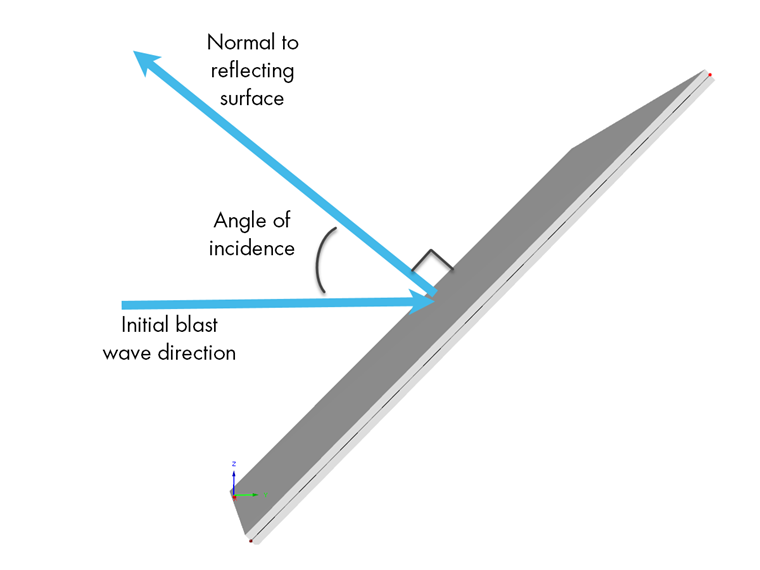
L'immagine sotto dimostra come l'angolo di incidenza può essere calcolato quando si considera la direzione iniziale dell'onda esplosiva e l'onda riflessa normale alla superficie.
Una volta determinato l'angolo di incidenza, la Figura 2-193 fornita nei Criteri delle Strutture delle United Facilities (UFC) 3-340-02 – Strutture per Resistere agli Effetti delle Esplosioni Accidentali [2] può essere utilizzata per fornire il valore Cr basato sul valore di sovrapressione di picco dell'incidente.
Storia semplificata della pressione-tempo del carico d'esplosione
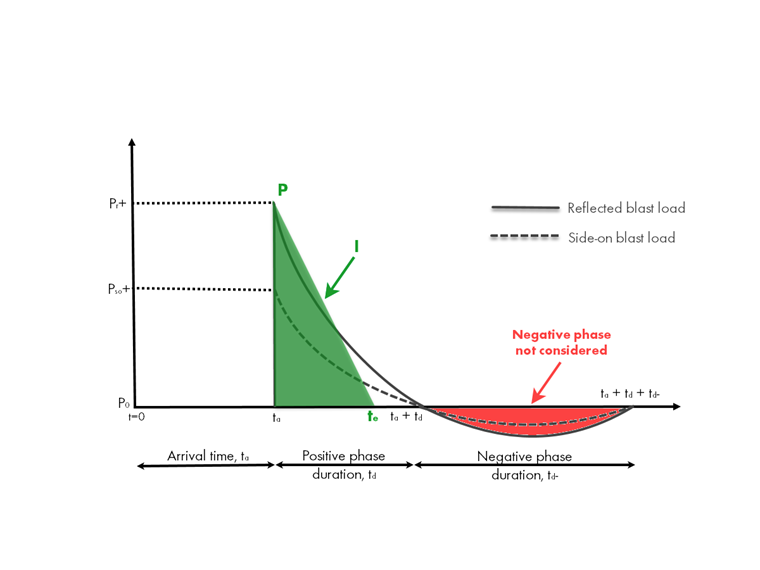
Ai fini progettuali, il grafico idealizzato mostrato sopra è semplificato in una distribuzione triangolare con un aumento istantaneo e un decadimento lineare sotto la fase positiva. Per mantenere la sovrapressione di picco dal grafico idealizzato così come l'impulso (area sotto la curva), una durata temporale fittizia, te, è approssimata come te = 2(I/P).
Estese ricerche per determinare il rapporto tra peso della carica, distanza di standoff (distanza dalla struttura all'esplosione) e i parametri dell'esplosione definiti nel grafico pressione-tempo sono state effettuate. I manuali tecnici come la risorsa [2] includono i parametri dell'esplosione aerea come funzione della distanza scalarizzata sotto forma di curve empiriche dei parametri d'esplosione.
La fase negativa è spesso ignorata per semplificazione con strutture semplici, dato che c'è poco impatto dall'analisi dell'esplosione. Tuttavia, la fase negativa diventa sempre più importante quando gli elementi della struttura sono più deboli nella direzione di carico inversa o hanno un periodo fondamentale breve rispetto alla durata del carico.
Variabili aggiuntive che possono avere un'influenza sull'analisi dell'esplosione ai fini di questo articolo non sono state prese in considerazione, come le forze di trascinamento dovute al vento o le pressioni dinamiche, la schermatura degli edifici adiacenti (riduzione del carico) e la riflessione (amplificazione del carico), e i carichi interni dovuti all'onda esplosiva che entra nelle aperture della struttura.
Guida alla progettazione AISC 26 – Esempio 2.1 in RFEM
La Guida alla progettazione AISC 26 – Esempio 2.1 [1] è un esempio di riferimento ideale per applicare l'analisi del carico d'esplosione in RFEM che segue le assunzioni sopra. La struttura d'esempio è un edificio in acciaio a un piano con dimensioni di 50 piedi (larghezza) ⋅ 70 piedi (lunghezza) ⋅ 15 piedi (altezza). Nella direzione corta della struttura, le cornici controventate sono modellate in RFEM come sezioni profilate a caldo W, mentre nella direzione lunga, anche le cornici rigide sono modellate con sezioni W. I traversi e le parenti sono modellati con sezioni C profilate a caldo. La facciata dell'edificio include pannelli metallici ondulati.
L'esplosione ha un peso di carica di 500 libbre e avviene a 50 piedi dalla facciata anteriore della struttura leggermente sopra il livello del suolo. Con queste informazioni, la distanza scalarizzata, Z, è quindi calcolata secondo la seguente equazione.
Parete Anteriore
Utilizzando la distanza scalarizzata, è possibile utilizzare la Figura 2-15 da [2] per determinare direttamente i parametri dell'onda esplosiva positiva per la pressione riflessa e laterale elencati di seguito nella Tabella 1.
| Parametro di carico d'esplosione | Dalla Figura 2-15 [2] | Valore calcolato |
|---|---|---|
| Pressione di picco riflessa (+) | Pr = 79.5 psi | - |
| Pressione di picco laterale (+) | Pso = 24.9 psi | - |
| Impulso riflesso (+) | Ir = 31.0W1/3 | Ir = 246 psi ms |
| Impulso laterale (+) | Iso = 12.1W1/3 | Iso = 96.0 psi ms |
| Tempo di arrivo | ta = 1.96W1/3 | ta = 15.6 ms |
| Durata del carico esponenziale (+) | td = 1.77W1/3 | td = 14.0 ms |
| Velocità del fronte d'urto | U = 1.75 ft/ms | - |
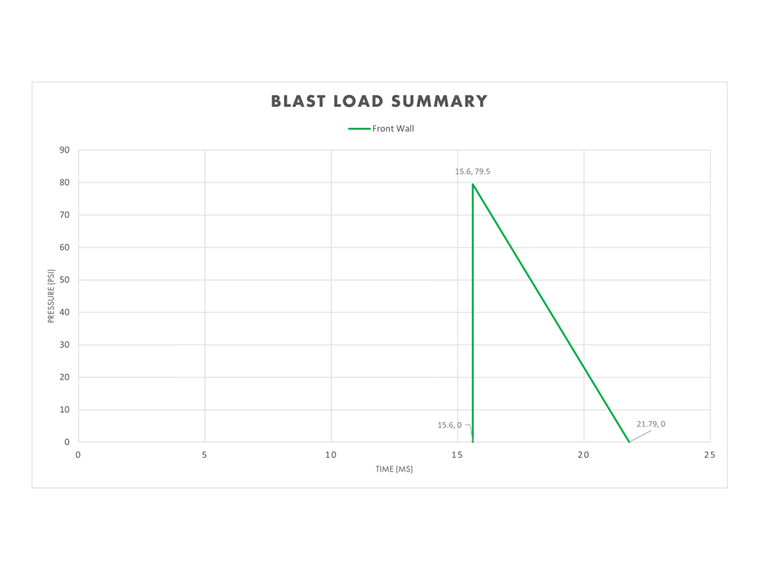
Poiché la parete frontale è direttamente rivolta verso l'esplosione iniziale, le variabili "riflesse" nella Tabella 1 sono applicabili a questa superficie. L'approccio triangolare semplificato richiede che la durata equivalente sia calcolata per garantire che l'impulso (area sotto la curva) sia preservato durante la fase di durata positiva.
te,r = 2Ir / Pr = 2(246 psi ms) / 29.5 psi = 6.19 ms
Il grafico iniziale della pressione-tempo è ora completo per la parete anteriore.
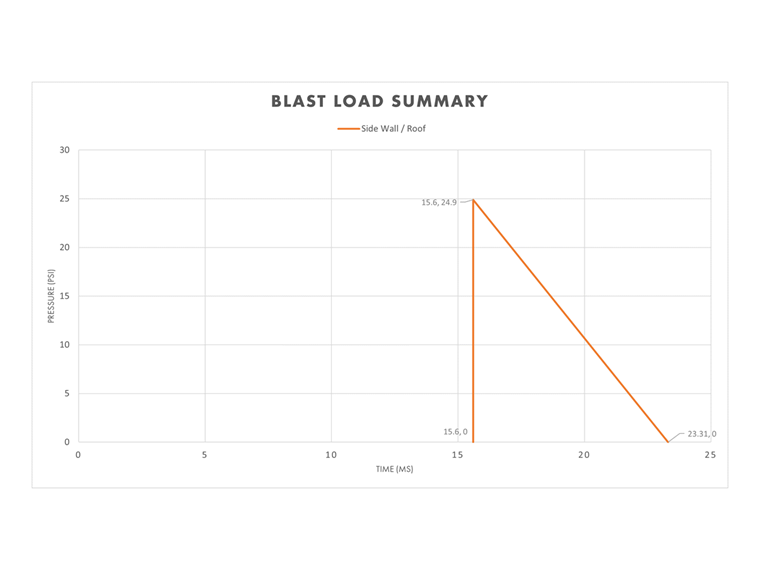
Pareti Laterali e Tetto
Per semplicità, la distanza scalarizzata, Z, calcolata per la parete anteriore viene utilizzata per determinare le variabili di esplosione per le pareti laterali e il tetto dell'edificio. Pertanto, i valori laterali nella Tabella 1 sopra vengono utilizzati per definire il grafico pressione-tempo per questa sezione dell'edificio. Un calcolo più dettagliato potrebbe essere eseguito per considerare la riduzione dell'onda esplosiva in funzione della distanza dalla parete laterale e dal tetto all'esplosione.
La durata equivalente, te, viene calcolata utilizzando le variabili laterali. te,so = 2Iso / Pso = 2(96.0 psi ms) / 24.9 psi = 7.71 ms
Parete Posteriore
La distanza scalarizzata, Z, per la parete posteriore è modificata per considerare la lunghezza aggiuntiva dell'edificio. La distanza è ora 50 piedi + 70 piedi per un totale di 120 piedi. Pertanto, Z è calcolata come segue.
|
R |
Distance from the element to charge |
|
W |
TNT equivalent charge weight |
La Figura 2-15 da [2] può essere utilizzata di nuovo per determinare i parametri dell'onda esplosiva positiva per la pressione laterale elencati di seguito nella Tabella 2.
| Parametro di carico d'esplosione | Dalla Figura 2-15 [1] | Valore calcolato |
|---|---|---|
| Pressione di picco laterale (+) | Pso = 4.60 psi | - |
| Impulso laterale (+) | Iso = 5.54W1/3 | Iso = 44.0 psi ms |
| Tempo di arrivo | ta = 8.32W1/3 | ta = 66.0 ms |
| Durata del carico esponenziale (+) | td = 3.11W1/3 | td = 24.7 ms |
| Velocità del fronte d'urto | U = 1.26 ft/ms | - |
La durata equivalente della parete posteriore, te, può essere calcolata con le variabili pertinenti sopra.
te,so = 2Iso / Pso = 2(44.0 psi ms) / 4.60 psi = 19.1 ms
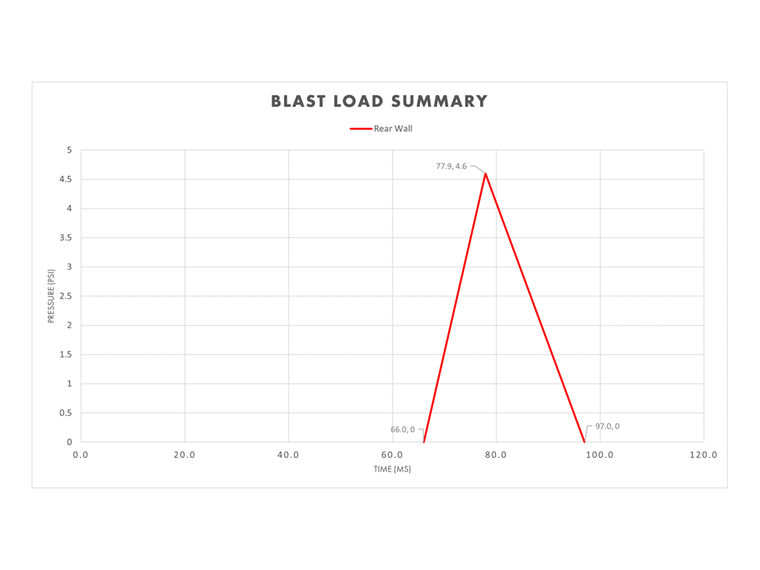
Poiché l'altezza della parete posteriore è di 15 piedi sopra il livello del suolo dove avviene l'esplosione, un aumento istantaneo della pressione non si verifica. Piuttosto, la velocità dell'onda esplosiva, l'altezza della parete posteriore e il tempo di arrivo vengono utilizzati per calcolare il tempo alla pressione di picco, t².
t2 = L1 / U + ta = 15.0 ft / 1.26 ft/ms + 66.0 ms = 77.9 ms
Il tempo fino alla fine del carico d'esplosione, tf, può ora essere determinato.
tf = t2 + te,so = 77.9 ms + 19.1 ms = 97.0 ms
Combinando tutte le variabili della parete posteriore calcolate sopra, il grafico pressione-tempo per questa sezione dell'edificio è completo.
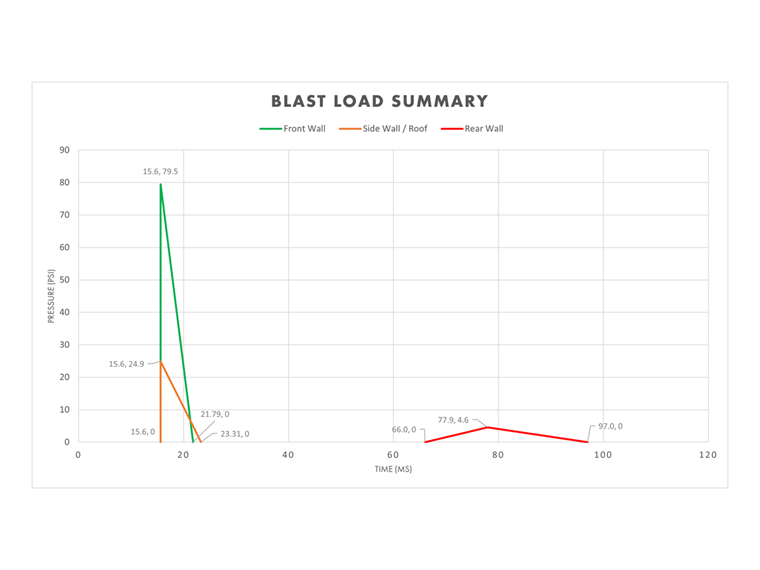
Sintesi del Carico d'Esplosione
Le pareti anteriori, laterali/tetto e posteriore possono essere compilate insieme per mostrare la pressione totale rispetto al tempo e illustrare come l'onda esplosiva influenzerà le diverse aree della struttura nel tempo.
Queste informazioni possono ora essere inserite in RFEM e nei moduli aggiuntivi RF-DYNAM Pro-Vibrazioni Forzate per le definizioni dei diagrammi temporali.
Applicazione in RFEM
Ora che i diagrammi pressione-tempo sono stati definiti per le varie sezioni dell'edificio, queste informazioni possono essere inserite nel modulo aggiuntivo RF-DYNAM Pro-Vibrazioni Forzate in RFEM.
RF-DYNAM Pro-Vibrazioni Naturali per determinare i periodi naturali, le frequenze e le forme modali della struttura è richiesto prima di eseguire l'analisi della storia temporale. Questa parte dell'analisi non è discussa in dettaglio ai fini di questo articolo.
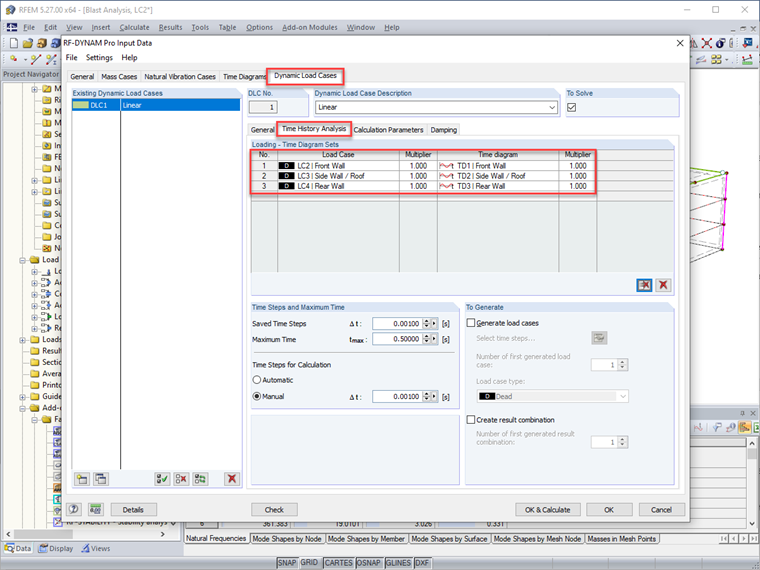
Per l'analisi della storia temporale, viene applicato un carico generico di area come tre casi di carico separati in RFEM per emulare la posizione del carico d'esplosione sulla struttura, inclusi LC1 – Parete Anteriore, LC2 – Parete Laterale/Tetto e LC3 – Parete Posteriore. Viene utilizzata una magnitudine di 1 kip/ft2 solo come segnaposto, poiché questo valore dipenderà successivamente dalla funzione della storia temporale.
In RF-DYNAM Pro-Vibrazioni Forzate, i diagrammi temporali sono definiti per ciascuna regione della struttura.
Si noti che ciascun diagramma temporale riflette le informazioni determinate sopra, come la pressione di picco e la durata equivalente per la parete anteriore, le pareti laterali/tetto e la parete posteriore.
Una volta definiti i diagrammi temporali, i carichi generali di area in RFEM sono direttamente collegati al diagramma pertinente.
Devono essere impostate anche variabili aggiuntive nel modulo aggiuntivo prima di eseguire l'analisi, come il solutore dell'analisi implicita lineare di Newmark, un tempo massimo di 0.5 secondi per la durata dell'analisi della storia temporale e un passo temporale di 0.001 secondi da utilizzare nel calcolo. Inoltre, utilizzando la frequenza angolare dei due modi più influenti, calcolati con l'analisi delle frequenze naturali insieme a un rapporto di smorzamento di Lehr del 2%, i coefficienti di smorzamento di Rayleigh α e β sono anch'essi impostati nel modulo.
Tutte le informazioni rilevanti sono ora definite per l'analisi della storia temporale dell'esplosione, e il calcolo di RFEM e RF-DYNAM Pro può essere eseguito. Strumenti di valutazione come il monitor delle dei corsi di tempo in RFEM possono essere utilizzati per valutare la risposta della struttura e la sicurezza durante l'esplosione dell'esplosione. Per una dimostrazione dettagliata dell'Esempio 2.1 della Guida alla progettazione AISC 26 in RFEM, fare riferimento al webinar precedentemente registrato Analisi della storia temporale delle esplosioni in RFEM.