AISC Steel Design Guide 26 - Design of Blast Resistant Structures [1] et plus précisément l'Exemple 2.1 - Évaluation préliminaire de la résistance aux explosions d'une structure à un étage est une référence essentielle pour diriger les ingénieurs ; s'appuyant sur une application de calcul de charge explosive simplifiée.
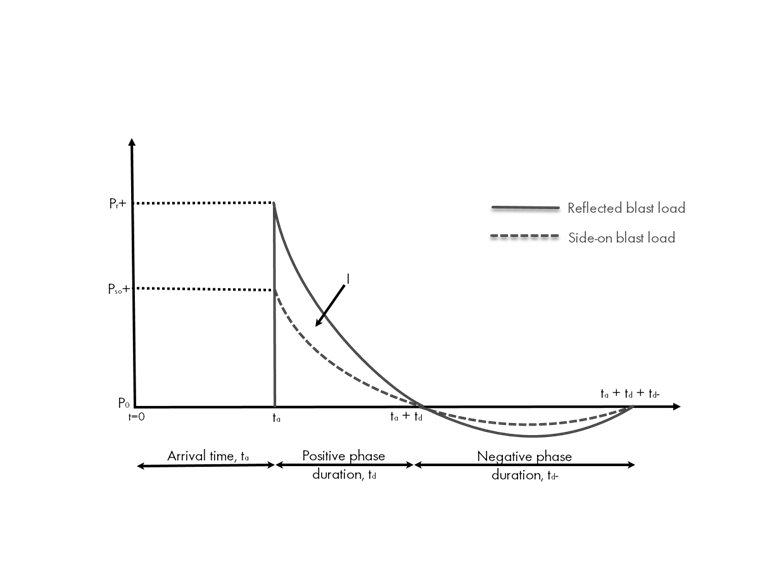
Diagramme idéalisé de l'historique pression-temps de la charge explosive
Le diagramme idéalisé de l'historique pression-temps affiche la variation de la force de pression suite à l'explosion.
Certains des paramètres essentiels sont directement générés dans le diagramme, notamment :
- Surpression maximale (Pr ou Pso) ... La pression instantanée atteignant la structure au-dessus de la pression atmosphérique.
- Durée de phase positive (td) ... Période durant laquelle la pression retombe au niveau de la pression ambiante.
- Impulsion positive (I) ... Le rapport total de l'énergie pression-temps appliqué pendant la durée positive est calculée à l'aide de la zone formée sous la courbe.
- Durée de phase négative (td-) ... Phase d'aspiration - période suivant la phase positive au cours de laquelle la pression chute en dessous de la pression atmosphérique.
Il est pertinent de remarquer que le diagramme idéalisé de l'historique pression-temps affiche deux courbes distinctes, incluant la « charge d'explosion latérale » et la « charge d'explosion réfléchie », indiquées respectivement par la ligne en pointillés et la ligne continue. La charge d'explosion latérale (également qualifiée de charge d'explosion en champ libre) inclut l'indice « so » couramment utilisé dans la littérature. Cela indique l'emplacement où la charge explosive traverse parallèlement une surface plutôt que perpendiculairement. Dans l'absolu, la charge balaiera la surface sans obstruction. Une paroi latérale parallèle à une charge explosive ou à une paroi arrière n'étant pas directement exposée à l'explosion en est un exemple.
La charge d'explosion réfléchie, indiquée par l'indice « r », se produit quant à elle lorsque l'onde de choc rencontre une surface inclinée non-parallèle. L'équation suivante peut être utilisée pour déterminer la pression réfléchie Pr.
Pr = Cr Pso
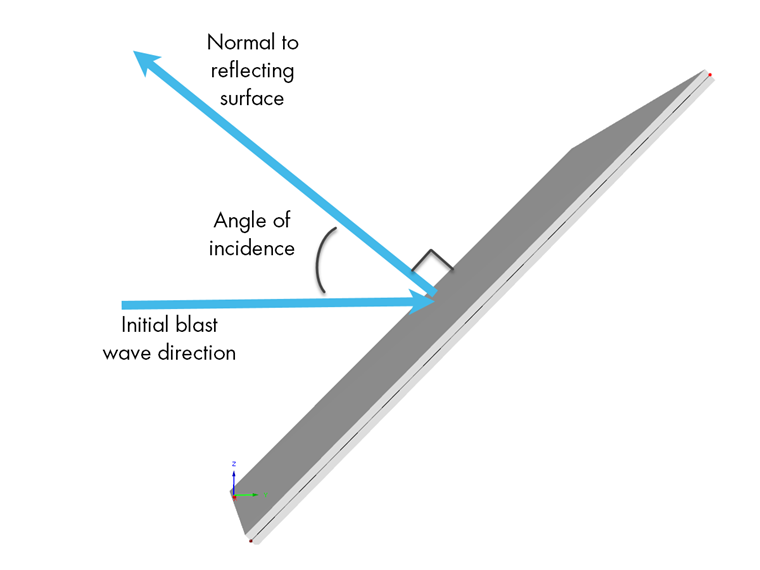
Pso est la pression latérale et Cr est le coefficient de réflexion. Cr est fonction de l'angle d'incidence ainsi que de la pression latérale. La figure ci-dessous affiche comment l'angle d'incidence peut être calculé en considérant la direction initiale de l'onde de choc additionnée à l'onde réfléchie perpendiculairement à la surface.
Une fois l'angle d'incidence déterminé, la Figure 2-193 contenue dans les Normes Communes de Structures (UFC) 3-340-02 - Structures résistantes aux dégâts provoqués par les explosions accidentelles [2] peut être exploitée pour déterminer la valeur de Cr, basée sur la surpression maximale incidente.
Diagramme simplifié de l'historique pression-temps de la charge explosive
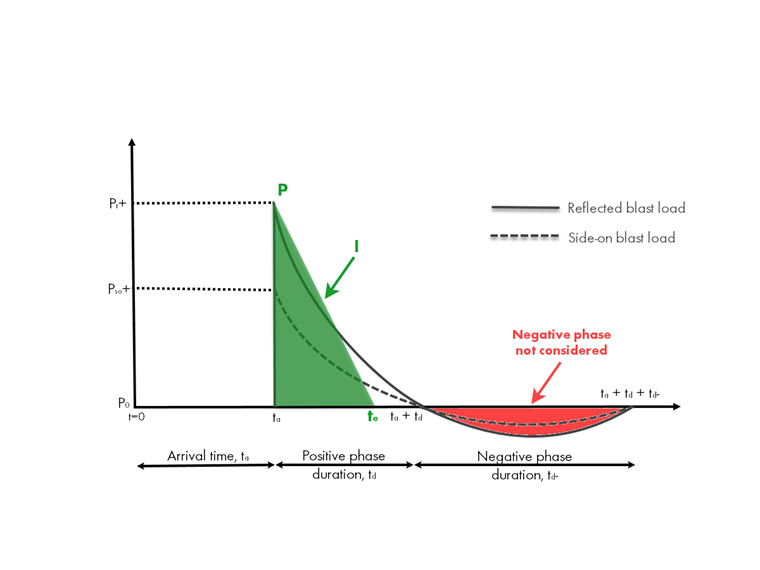
Pour des raisons de calcul, le diagramme idéal décrit ci-dessus est simplifié sous forme de distribution triangulaire illustrée par une croissance instantanée ainsi qu'un déclin linéaire sous la phase positive. Afin de conserver la surpression maximale du diagramme idéal ainsi que l'impulsion (zone sous la courbe), une durée fictive te avec te = 2 (I/P) est estimée.
Des études approfondies ont été menées pour déterminer la relation entre le poids de la structure, la distance entre le bâtiment et l'explosion et les paramètres d'explosion définis dans le diagramme affichant le rapport pression-temps. Des manuels techniques tels que la Source [2], intègrent les paramètres du souffle généré par l'explosion en fonction de la distance convertie sous forme de courbes de paramètres d'explosion empiriques.
Afin de simplifier la démarche de calcul, la phase négative n'est souvent pas prise en compte dans le cas de structures simples, car l'analyse des explosions a peu d'influence sur ce processus. Cependant, la phase négative gagne progressivement en importance lorsque les éléments structuraux sont plus faibles dans la direction de charge inversée ou lorsqu'ils témoignent d'une durée initiale réduite par rapport à la durée de charge.
D'autres variables susceptibles d'avoir une influence sur l'analyse des explosions aux fins de cet article n'ont pas été prises en compte, telles que les forces de traînée dues aux pressions de vent ou dynamiques, le blindage des bâtiments adjacents (réduction de charge) et la réflexion (amplification de charge). les charges intérieures dues à l'onde de choc entrant dans les ouvertures de la structure.
AISC Design Guide 26- Exemple 2.1 dans RFEM
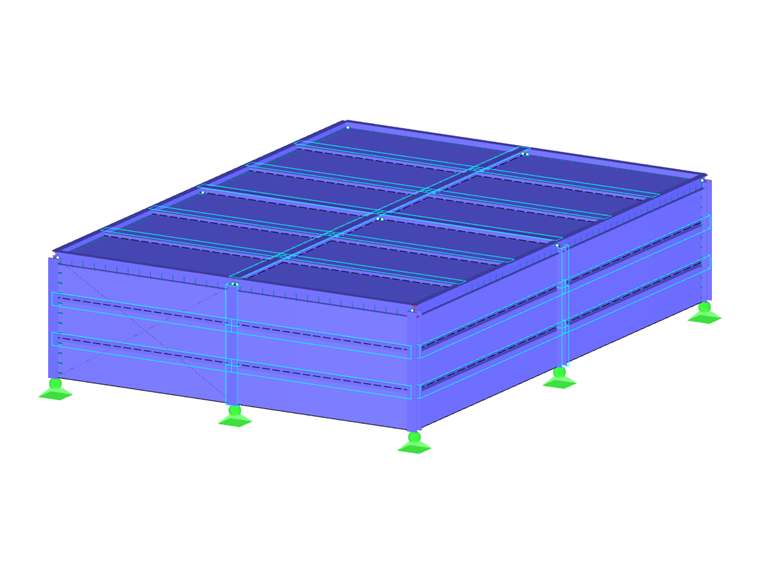
AISC Design Guide 26- Exemple 2.1 [1] est un exemple de référence essentiel pour appliquer l'analyse des charges d'explosion dans RFEM, en s'appuyant sur les hypothèses ci-dessus. L'exemple de structure proposé se présente sous la forme d'un bâtiment en acier à un étage de 50 pieds de long sur 70 pieds de large et de 15 pieds de haut. Dans la direction courte du bâtiment, les portiques fixes sont modélisés sous forme de profilés en W laminés à chaud dans RFEM, à l'instar des portiques rigides également modélisés avec des profilés en W dans la direction longue. Les poutres intermédiaires et les pannes sont modélisées avec des profilés en C laminés à chaud. La façade du bâtiment est composée de bacs en acier trapézoïdaux.
L'explosion se définit par un poids d'une grandeur de 500 lbs et se produit légèrement au-dessus du sol, à environ 50 pieds de l'avant de la structure. Avec ces informations, la distance Z convertie à l'échelle souhaitée est calculée selon l'équation ci-dessous.
| r | Distance entre l'élément et le chargement |
| W | Poids de charge équivalent en TNT |
Façade
En s'appuyant sur la distance convertie, les paramètres de l'onde de choc positive listés ci-dessous dans le tableau 1 en rapport avec la pression réfléchie et la pression latérale peuvent être déterminés directement à l'aide de la Figure 2-15 de [2].
| Paramètres de charge d'explosion | Voir la Figure 2-15 [2] | Valeur Calculée |
|---|---|---|
| Pression maximale réfléchie (+) | Pr = 79,5 psi | - |
| Pression maximale latérale (+) | Pso = 24,9 psi | - |
| Impulsion réfléchie (+) | Ir = 31,0W 1/3 | Ir = 246 psi ms |
| Impulsion latérale (+) | Iso = 12,1W 1/3 | Iso = 96,0 psi ms |
| Heure de l'explosion | ta = 1,96W 1/3 | ta = 15,6 ms |
| Durée de charge exponentielle (+) | td = 1,77W 1/3 | td = 14,0 ms |
| Impact de vélocité frontale | U = 1,75 pi/ms | - |
Comme la surface avant fait directement face à l'explosion initiale, les variables « réfléchies » du tableau 1 s'appliquent à celle-ci. La distribution triangulaire simplifiée nécessite que la durée équivalente soit calculée afin de s'assurer que l'impulsion (zone générée sous la courbe) soit maintenue pendant la phase de durée positive.
te,r = 2Ir / Pr = 2 (246 psi ms) / 29,5 psi = 6,19 ms
L'affichage initial du rapport pression-temps pour la façade est maintenant entièrement généré.
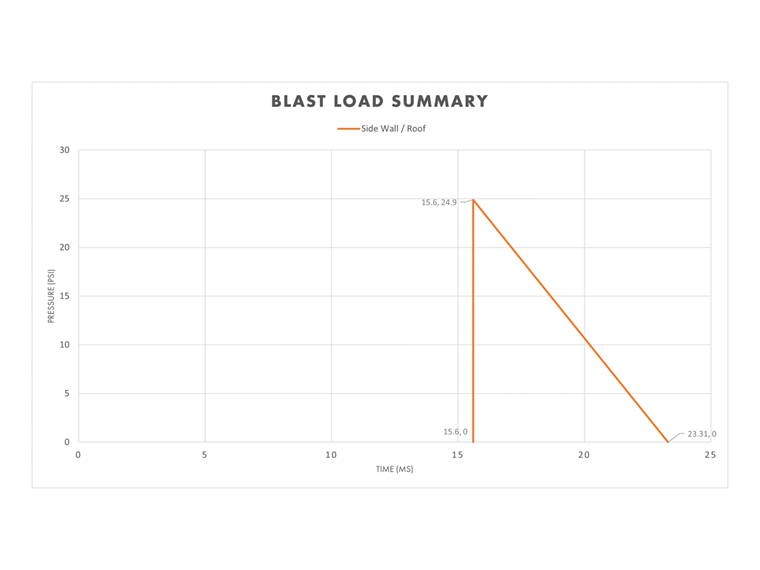
Parois latérales et toiture
Pour simplifier la démarche de calcul, la distance Z estimée par rapport à la paroi avant est utilisée pour déterminer les variables d'explosion associées aux parois latérales ainsi qu'à la toiture du bâtiment. Par conséquent, les valeurs latérales affichées dans le tableau 1 ci-dessus sont utilisées pour définir le rapport pression-temps pour cette section de bâtiment dans le diagramme. Un calcul plus détaillé peut être effectué afin de considérer la réduction de l'onde de choc en fonction de la distance entre les parois latérales, la toiture et l'explosion.
La période d'équivalence te est calculée à l'aide des variables latérales.
te, so = 2Iso / Pso = 2 (96,0 psi ms) / 24,9 psi = 7,71 ms
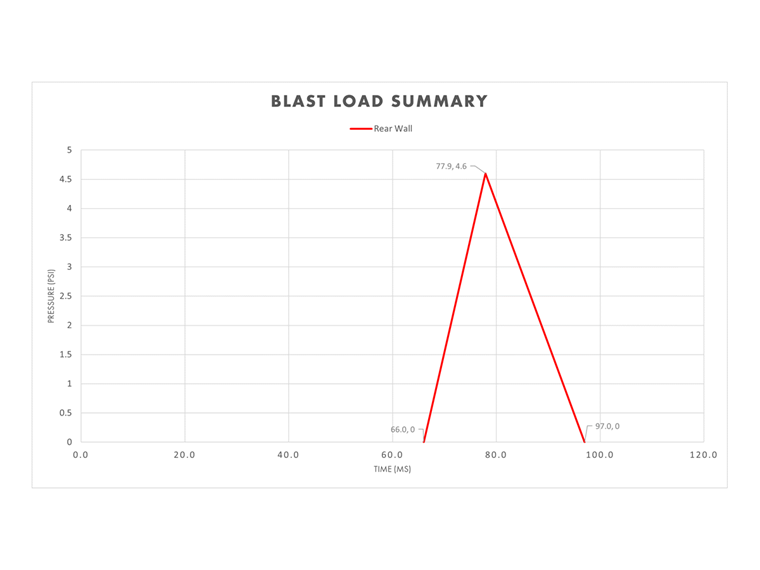
Paroi arrière
La distance Z convertie à l'échelle souhaitée et associée à la paroi arrière est modifiée pour tenir compte de la longueur supplémentaire du bâtiment. La distance est désormais égale à 50 pieds + 70 pieds pour un total de 120 pieds. Par conséquent, Z est calculé de cette façon :
| r | Distance entre l'élément et le chargement |
| W | Poids de charge équivalent en TNT |
La Figure 2-15 provenant de [2] peut être à nouveau utilisée pour déterminer les paramètres de l'onde de choc positive par rapport à la pression latérale listés dans le tableau 2 ci-dessous.
| Paramètres de charge d'explosion | Voir la Figure 2-15 [2] | Valeur calculée |
|---|---|---|
| Pression maximale latérale (+) | Pso = 4,60 psi | - |
| Impulsion latérale (+) | Iso = 5,54W1/3 | Iso = 44,0 psi ms |
| Heure de l'explosion | ta = 8,32W1/3 | ta = 66,0 ms |
| Durée de charge exponentielle (+) | td = 3,11W1/3 | td = 24,7 ms |
| Impact de vitesse antérieur | U = 1,26 pi/ms | - |
La période équivalente te associée à la paroi arrière peut être calculée à l'aide des variables appropriées mentionnées ci-dessus.
te,so = 2Iso / Pso = 2 (44,0 psi ms) / 4,60 psi = 19,1 ms
Étant donné que la hauteur de la paroi arrière est de 15 pieds supérieure à la hauteur du terrain où l'explosion se produit, il n'y a pas d'augmentation immédiate de la pression. La vitesse de l'onde de choc, la hauteur de la paroi arrière et l'heure de l'explosion sont plus susceptibles d'être utilisées pour déterminer le temps écoulé jusqu'à la pression maximale t2.
t2 = L1 / U + ta = 15,0 pi / 1,26 pi/ms + 66,0 ms = 77,9 ms
Il est désormais possible de déterminer le temps écoulé jusqu'à la fin de la charge d'explosion tf.
tf = t2 + te,so = 77,9 ms + 19,1 ms = 97,0 ms
Si toutes les tailles de parois arrières calculées ci-dessus sont combinées, le diagramme de rapport pression-temps associé à cette section de bâtiment est achevé.
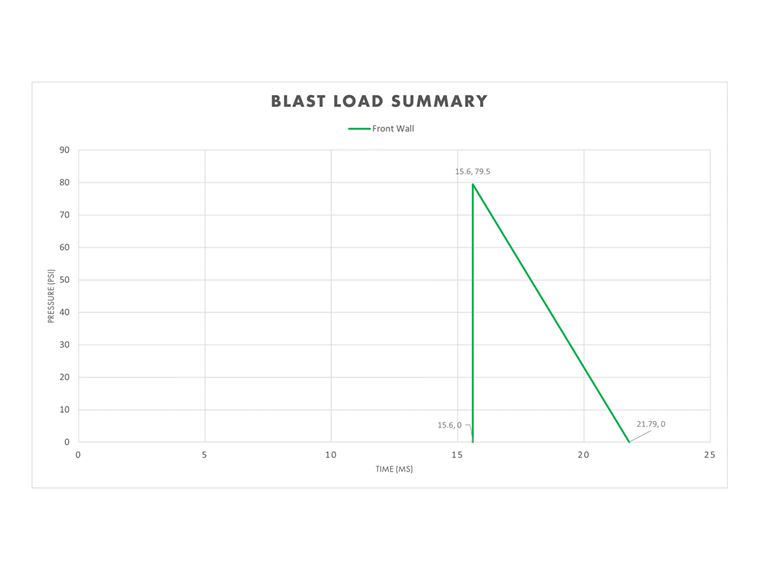
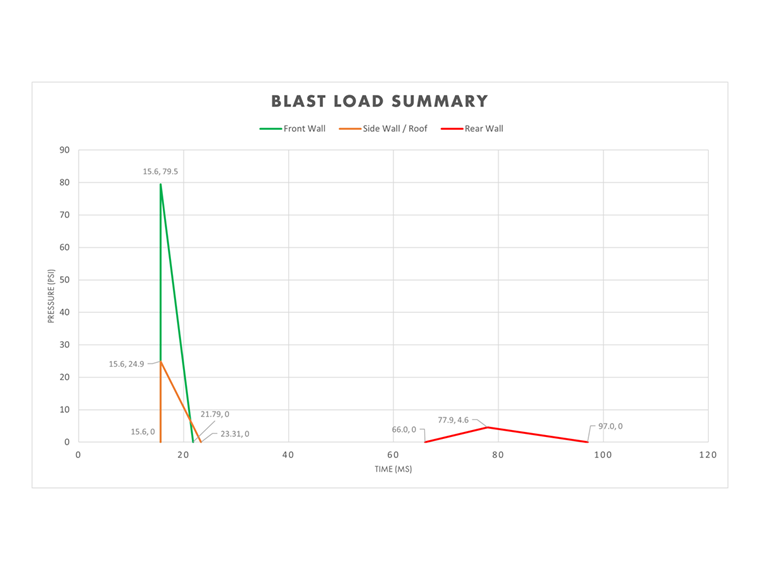
Résumé de la charge d'explosion
Les paramètres de la toiture, des parois avant, latérales et arrière peuvent être respectivement compilés afin d'afficher la pression totale en fonction du temps écoulé, illustrant ainsi comment l'onde de choc affecte les différentes zones de la structure au fil du temps.
Ces informations peuvent maintenant être importées dans RFEM et dans le module additionnel RF-DYNAM Pro-Forced Vibrations afin d'établir graphiquement la chronologie des évènements.
Application dans RFEM
Une fois les diagrammes de rapport pression-temps établis pour les différentes sections du bâtiment, ces informations peuvent être transférées dans le module additionnel RF-DYNAM Pro-Forced Vibrations de RFEM.
Toutefois, le module additionnel RF-DYNAM Pro-Natural Vibrations est nécessaire pour déterminer les périodes propres de la structure ainsi que les fréquences et le mode propre de la structure avant que l'analyse chronologique des faits ne puisse être effectuée. Cette étape de l'analyse n'est cependant pas détaillée par souci de cohérence avec cet article technique.
Concernant l'analyse chronologique des faits, une charge surfacique globale générée sous forme de trois cas de charge distincts est appliquée dans RFEM pour simuler l'emplacement de la charge d'explosion impactant la structure, incluant CC1 - paroi avant, CC2 - paroi latérale/toit et CC3 - paroi arrière. Un ordre de grandeur de 1 kip/pi2 est uniquement utilisé comme paramètre temporaire, car cette valeur dépendra ensuite des éléments fournis par l'historique des faits.
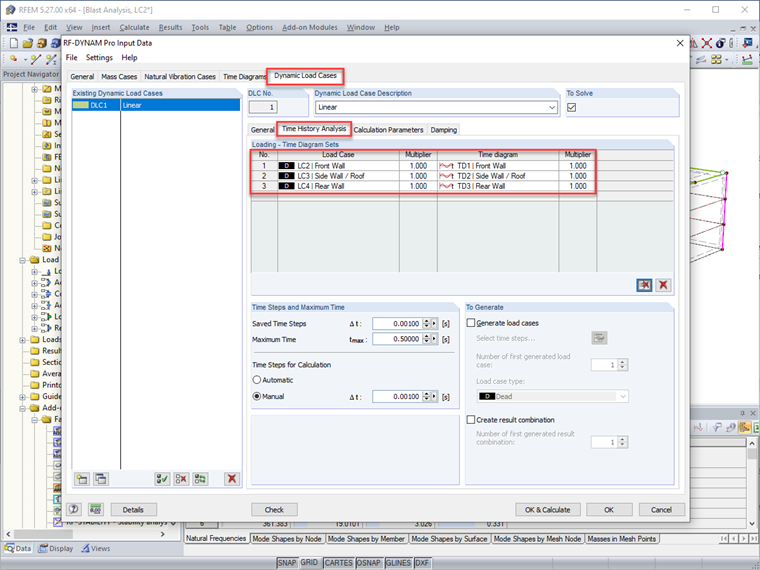
Dans RF-DYNAM Pro-Forced Vibrations, les diagrammes affichant la chronologie des faits sont respectivement établis pour chaque zone de la structure.
Veuillez noter que chaque diagramme de temps reflète les informations déterminées ci-dessus, telles que la pression maximale et la durée équivalente pour les parois avant, les parois latérales/de toiture et la paroi arrière.
Une fois que la chronologie des faits a été graphiquement établie, les charges surfaciques globales générées dans RFEM sont directement associées au diagramme correspondant.
Des variables supplémentaires doivent être définies dans le module additionnel avant de lancer l'analyse, telles que le solveur d'analyse linéaire implicite Newmark, un temps maximal de 0,5 secondes pour la durée de l'analyse de l'historique de temps et un pas de temps de 0,001 secondes à utiliser dans le calcul. De plus, en utilisant la fréquence angulaire des deux modes déterminants calculées avec l'analyse des fréquences propres avec un rapport d'amortissement de Lehr de 2 %, les coefficients d'amortissement de Rayleigh a et β sont également définis dans le module.
Toutes les informations pertinentes pour l'analyse de l'historique des explosions sont maintenant définies et les calculs de RFEM et RF-DYNAM Pro peuvent être exécutés. Grâce à certains outils d'évaluation, tel que le dispositif de contrôle de l'historique des faits dans RFEM, les facteurs de résistance et de réactivité de la structure peuvent être évalués au cours de l'explosion. Pour une démonstration complète de l'exemple 2.1 du Guide de calcul AISC 26 2.1 [1] dans RFEM, se référer au webinaire traitant de l'analyse de l'historique des explosions dans RFEM.
