Endommagement du modèle de matériau non linéaire

Surfaces d'élasticité dans RFEM (von Mises, Tresca, Drucker-Prager, Mohr-Coulomb)

Leurs règles d'élasticité ne peuvent donc s'appliquer qu'au comportement de matériau élastique-plastique pur. Pour les matériaux soumis à un processus d'endommagement par des fissures, par exemple, le modèle de matériau décrit ci-dessous est plus approprié. Un bon exemple d'un tel matériau est le béton, qui présente une résistance à la compression nettement plus élevée par rapport à la résistance à la traction. Les fissures qui se produisent dans la zone en traction du matériau réduisent la rigidité du système. Dans le cas du béton armé ou du béton fibré, les armatures absorbent les efforts en traction.

Principes théoriques

Les modèles de matériaux non linéaires sont généralement représentés en déplaçant le système dans l'espace déformé actuel vers une configuration de référence sans contrainte (voir la Figure 02). Vous trouverez par exemple plus d'informations à ce sujet dans [2].

Relation cinématique entre la configuration de référence et la configuration actuelle (source: [1])

Les déformations de l'élément local sont représentées dans le système de référence à l'aide d'un tenseur de déformation. Les déformations dans le système de référence non déformé peuvent être calculées à l'aide du tenseur des déformations de Green-Lagrange E = ½ ∙ (F^T ∙ F - 1) et les déformations dans le système de coordonnées local à l'aide du tenseur des déformations d'Euler-Almansi e = ½ ∙ ( I - b^-1 ). De ces deux déformations, la déformation linéaire ε = ½ ∙ (H + H^T ) est obtenue à l'aide de l'intégration partielle et est utilisée pour calculer les contraintes nominales sur le système à l'aide du théorème de Cauchy et du tenseur des contraintes de Piola-Kirchhoff. Ainsi, les taux d'énergie libre peuvent être déterminés à l'aide des équations d'équilibre du continu.

Équations d'équilibre du continu :

• L'équilibre de masse signifie que la masse du système reste la même, même si elle est déformée.
  
  $$\mathrm{m} = {\int }_{\mathrm{Bt}}\mathrm{\rho d\nu } (\mathrm{verformtes} S\mathrm{ystem}) = {\int }_{\mathrm{B}0}\mathrm{dV} \left(\mathrm{Referenzsystem}\right) = \mathrm{konstant}$$

  Formule 1
• Équilibre des moments comme un changement temporel de la quantité de mouvement totale
  
  $$\frac{\mathrm{d}}{\mathrm{dt}}{\int }_{\mathrm{Bt}}\mathrm{\rho ẋd\nu } = {\int }_{\mathrm{Bt}}\mathrm{\rho bd\nu } \left(\mathrm{Volumenkräfte}\right) {\int }_{\mathrm{\delta Bt}}\mathrm{tda} \left(\mathrm{Oberflächenkräfte}\right)$$

  Formule 2
• Équilibre du moment angulaire comme une vitesse de changement de vitesse du moment total
  
  $$\frac{\mathrm{d}}{\mathrm{dt}} {\int }_{\mathrm{Bt}}\mathrm{\rho x} · \mathrm{ẋd\nu } = {\int }_{\mathrm{Bt}}\mathrm{\rho } (\mathrm{x} · \mathrm{b}) \mathrm{d\nu } {\int }_{\mathrm{\delta Bt}}\mathrm{x} · \mathrm{td}$$

  Formule 3
• 1. loi de la thermodynamique : L'énergie totale d'un système est constante.
  
  $$\frac{\mathrm{d}}{\mathrm{dt}}{\int }_{\mathrm{Bt}}(\mathrm{u} \frac{1}{2} · \mathrm{ẋ} · \mathrm{ẋ}) \mathrm{\rho d\nu } = {\int }_{\mathrm{Bt}}\mathrm{\rho r} \mathrm{b} · \mathrm{ẋd\nu } {\int }_{\mathrm{\delta Bt}}\mathrm{t} · \mathrm{ẋ} - \mathrm{q} · \mathrm{nda}$$

  Formule 4
  
  énergie cinétique = puissance mécanique + contrainte de surface
• Deuxième loi de la thermodynamique : Lors d'un transfert vers un autre plan, l'énergie (thermie) est libérée.
  
  $$\frac{\mathrm{d}}{\mathrm{dt}}{\int }_{\mathrm{Bt}}\mathrm{\rho sd\nu } \ge {\int }_{\mathrm{Bt}}\mathrm{\rho } \frac{\mathrm{r}}{\mathrm{\theta }} \mathrm{\nu } - {\int }_{\mathrm{\delta Bt}}\frac{1}{\mathrm{\theta }} \mathrm{q} · \mathrm{nda}$$

  Formule 5

Les équations d'état (équations de comportement) décrivent la relation entre les matériaux. Les variables internes (énergie libre ψ, entropie spécifique s, tenseur des contraintes de Cauchy σ, vecteur de flux thermique q) sont utilisées pour considérer les dommages dans le modèle de matériau. La « mémoire » du matériau, son comportement en fonction du temps, joue également un rôle important. Ceci est pris en compte par l'écrouissage cinématique et isotrope. En ce qui concerne les dommages causés au matériau, le composant de déformation est décomposé en une partie élastique et plastique. La partie plastique est à nouveau décomposée en partie cinématique et isotrope.
ε = ε^e + ε^p → ε^p = ε^iso + ε^kine

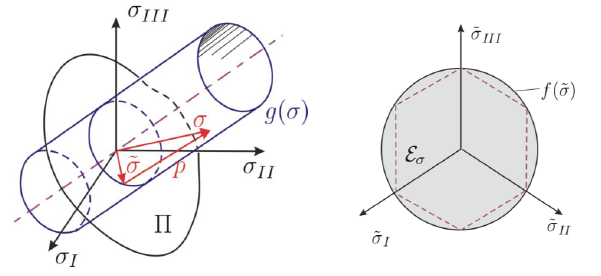
Dans cet article sur le comportement non linéaire des matériaux, nous vous avons expliqué que la fonction du fluage, qui prend en compte les effets d'endommagement, dépend des invariables du tenseur de contrainte. Plus précisément, la fonction d'élasticité est déterminée par une condition dite de Kuhn-Tucker, qui stipule que tous les états de contrainte dans l'espace des contraintes principales sont inférieurs à 0 et donc élastiques. Les contraintes en dehors de cette zone ne sont pas autorisées et sont projetées dans la surface d'élasticité lors de l'étape de correction (étape facteur-corrigeur). Ce calcul est effectué à titre de test, ce qui nécessite la méthode de calcul non linéaire selon Newton-Raphson.

Grafische Darstellung der Fließfläche im Hauptspannungsraum

La fonction d'élasticité (issue de [4] ) du modèle de matériau Endommagement permet de distinguer le matériau de la contrainte de traction et de la contrainte de compression :

Dans ce cas, r est le débit d'énergie et h le durcissement de la fonction. Les variables A et B indiquent l'endommagement du matériau. Cette opération est similaire au chapitre suivant à l'aide d'un diagramme contrainte-déformation dans l'espace des contraintes principales.

Endommagement dans RFEM

Après une introduction basique du sujet, cet article explique comment gérer le modèle de matériau dans RFEM. Dans cet article, nous ne pouvons fournir qu'un aperçu grossier, il peut donc y avoir des écarts dans le contexte. Pour cette raison, il est recommandé de consulter d'autres ouvrages tels que [2].

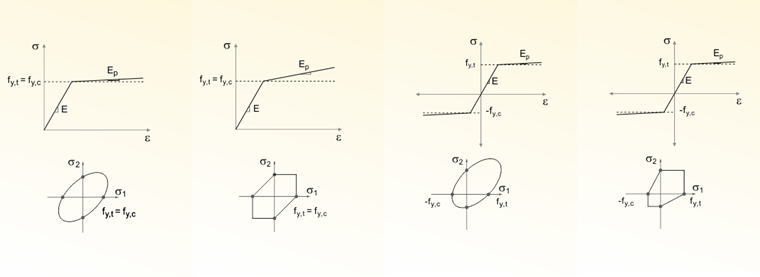
En raison de la méthode de calcul non linéaire avec l'étape de correction, il est nécessaire d'effectuer le calcul linéaire élastique dans la première étape du diagramme. La solution dans RFEM fournit la déformation dans la deuxième étape du diagramme en fonction du module d'élasticité, qui est défini dans la boîte de dialogue du matériau, et de la contrainte limite définie (voir la Figure 04).

Eingabe der Spannungs-Dehnungs-Beziehung in RFEM

Dans ce cas, la déformation est déterminée par la loi de Hooke ε = σ/E. Après cette première étape de visualisation élastique, vous pouvez effectuer une définition antimétrique presque arbitraire du diagramme contrainte-déformation. Il est également possible que le module d'élasticité du matériau soit négatif, étant donné qu'il est recalculé comme suit :

Cependant, étant donné que le module élastique n'est nécessaire que pour recalculer la relation, la quantité du module est également autorisée. Dans le cas du modèle de matériau Endommagement, le calcul décrit par itération de correction garantit que la rigidité du système est réduite jusqu'à ce que l'élément EF n'absorbe plus de contrainte. Les déformations dans l'élément concerné peuvent être très importantes.

Résumé

Le modèle de matériau Endommagement permet un calcul non linéaire avec des diagrammes de contrainte-déformation antimétriques et presque arbitraires. Cependant, si le matériau est endommagé, le système reste entier. C'est-à-dire qu'aucune fissure ne se produit dans le système. L'effort numérique serait très considérable pour cela. Par exemple, il est nécessaire de générer un nouveau maillage du système avec un maillage EF adaptatif. En raison de ces limites, de très grandes déformations peuvent survenir dans le système.

Dans le cas de déformations très élevées, vous pouvez diviser le système manuellement. Les solides de contact avec la même limite d'élasticité peuvent être utilisés à cet effet. De plus, une distorsion plastique de l'élément n'est pas considérée lors de l'utilisation de ce modèle de matériau, ce qui peut être particulièrement utile dans la zone de compression. Le modèle de matériau est suffisamment précis pour le problème courant du béton fissuré dans la zone de traction.

Références