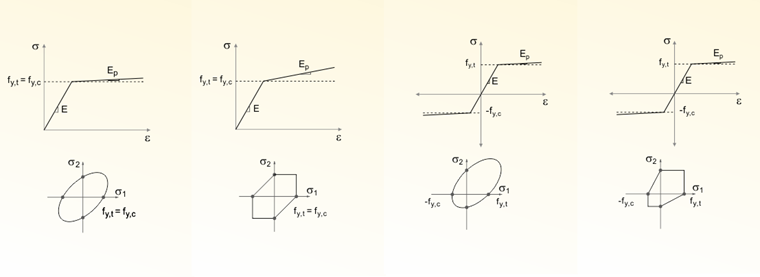
Dlatego reguły uplastycznienia mogą mieć zastosowanie tylko do czysto sprężysto-plastycznego zachowania materiału. Für Materialien, die einem Schädigungsprozess durch zum Beispiel Risse unterliegen, ist das nachfolgend erläuterte Materialmodell Schädigung besser geeignet. Ein gutes Beispiel für solch ein Material ist Beton, der eine wesentlich höhere Druckfestigkeit gegenüber der Zugfestigkeit besitzt. Durch Risse, die im Zugbereich des Materials auftreten, wird die Steifigkeit des Systems verringert. Bei bewehrtem Beton oder Stahlfaserbeton nimmt in diesem Fall die Bewehrung die Zugspannungen auf.
Podstawy teoretyczne
Nichtlineare Materialmodelle werden im allgemeinen über die Verschiebung eines Körpers im verformten aktuellen Raum zu einer spannungsfreien Referenzkonfiguration abgebildet (siehe Bild 02). Weiterführende Informationen zu dieser Thematik finden sich beispielsweise in [2].
Über einen Verzerrungstensor werden die Verformungen des lokalen Elements im Referenzsystem abgebildet. Die Verzerrung im unverformten Referenzsystem wird dabei über den Green-Lagrange-Verzerrungstensor E = ½ ∙ (FT ∙ F - 1) und die Verzerrung im lokalen Koordinatensystem über den Euler-Almansi-Verzerrungstensor e = ½ ∙ (I - b-1) hergeleitet. Aus diesen beiden Verzerrungen wird über partielle Integration eine lineare Verzerrung ε = ½ ∙ (H + HT) abgeleitet, aus welcher über das Cauchy-Theorem und den Piola-Kirchhoff-Spannungstensor die nominellen Spannungen auf den Körper berechnet werden können. Über die Bilanzgleichungen des Kontinuums können somit freie Energieraten abgebildet werden.
Bilanzgleichungen des Kontinuums:
- Die Massenbilanz besagt, dass die Masse des Systems gleich bleibt auch wenn es sich verformt.
- Impulsbilanz als zeitliche Änderung des Gesamtimpulses
- Drehimpulsbilanz als Änderungsgeschwindigkeit des Gesamtimpulses
- 1. Hauptsatz der Thermodynamik: Gesamtenergie eines Körpers bleibt erhalten.
kinetische Energie = mechanische Leistung + Spannung Oberfläche - Drugi Hauptsatz der Thermodynamik: Beim Übergang in eine andere Ebene wird Energie (Wärme) frei.
Mit den Zustandsgleichungen (Konstitutivgleichungen) wird die Materialabhängigkeit der Körper eingeführt. Über die inneren Variablen (freie Energie ψ, spezifische Entropie s, Cauchy-Spannungstensor σ, Wärmeflussvektor q) wird die Schädigung im Materialmodell berücksichtigt. In diesem Zusammenhang spielt auch das "Gedächtnis" des Materials eine wichtige Rolle, also sein zeitabhängiges Verhalten. Dies wird über kinematische und isotrope Verfestigung berücksichtigt. Im Hinblick auf die Schädigung des Materials wird der Verzerrungsanteil in einen elastischen und plastischen Anteil additiv zerlegt. Der plastische Anteil hieraus wird wiederum in einen kinematischen und isotropen Anteil zerlegt.
ε = εe + εp → εp = εiso + εkin
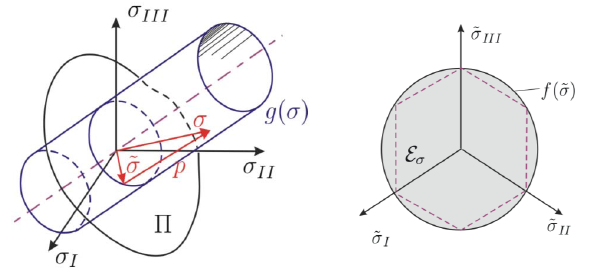
Im Beitrag zum nichtlinearen elastischen Materialverhalten wurde bereits erläutert, dass die Fließfunktion, welche die Schädigungseffekte berücksichtigt, von den Invarianten des Spannungstensors abhängig ist. Konkret unterliegt die Fließfunktion einer Beschränkung nach der sogenannten Kuhn-Tucker-Bedingung die besagt, dass alle Spannungszustände innerhalb des Hauptspannungsraums kleiner 0 und damit elastisch sind. Spannungen außerhalb dieses Raumes sind unzulässig und werden über einen Korrekturschritt (Prädiktor-Korrektor-Schritt) wieder auf die Fließfläche zurück projiziert. Diese Berechnung erfolgt über eine Testfunktion, was eine nichtlineare Berechnungsmethode nach Newton-Raphson notwendig macht.
Die Fließfunktion (aus [4]) im Materialmodell Schädigung unterscheidet für das Material zwischen Zug- und Druckbeanspruchung:
Mit r wird hierbei die Energierate und mit h die Verfestigung der Funktion gekennzeichnet. Die Variablen A und B bezeichnen die Schädigung des Materials. Dies wird analog zum nächsten Kapitel ebenfalls über die Spannungs-Dehnungs-Beziehung im Hauptspannungsraum durchgeführt.
Schädigung in RFEM
Nach dieser grundlegenden Einführung in die Thematik wird die Behandlung des Materialmodels in RFEM erläutert. Im Rahmen dieses Beitrags ist nur eine grobe Übersicht zur Thematik möglich, welche auch Lücken im Zusammenhang aufweisen kann. Daher wird weiterführende Literatur wie [2] empfohlen.
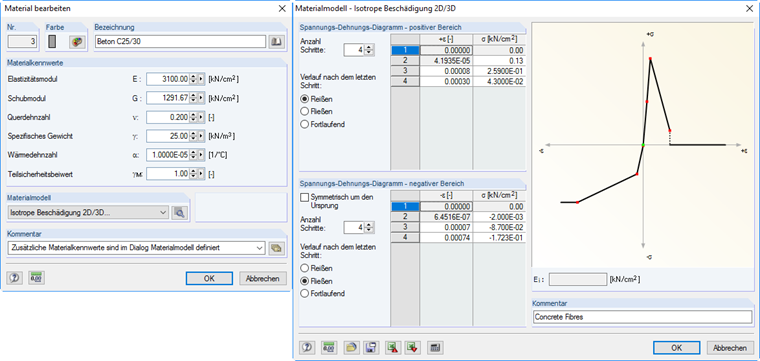
Aufgrund der nichtlinearen Berechnungsmethode mit Korrekturschritt muss die Berechnung in der ersten Stufe des Diagramms linear elastisch erfolgen. Die Lösung in RFEM hierzu sieht vor, dass die Dehnung in der zweiten Stufe des Diagramms abhängig von dem im Materialdialog definierten E-Modul und der definierten Grenzspannung ist (siehe Bild 04).
Die Dehnung unterliegt hierbei dem Hookeschen Gesetz ε = σ / E. Nach diesem ersten elastischen Prediktorschritt kann eine nahezu beliebige antimetrische Definition des Spannungs-Dehnungs-Diagramms erfolgen. Hierbei ist es auch möglich, dass der E-Modul des Materials negativ wird, da dieser über folgende Beziehung zurückgerechnet wird:
Da der E-Modul jedoch lediglich zur Rückrechnung der Beziehung notwendig ist, ist hier auch der Betrag des Moduls möglich. Die ebenfalls erläuterte Berechnung über eine Korrekturiteration sorgt beim Materialmodell Schädigung dafür, dass die Steifigkeit des Systems solange verringert wird, bis jedes einzelne FE-Element keine Spannung mehr aufnimmt. Die Dehnungen im jeweiligen Element können hierbei sehr groß werden.
Podsumowanie
Mit dem Materialmodell Schädigung ist die nichtlineare Berechnung mit antimetrischen, nahezu beliebigen Spannungs-Dehnungs-Beziehungen möglich. Erfolgt eine Schädigung des Materials, bleibt das System aber weiterhin ein Kontinuum. Das heißt, es werden keine Risse im System abgebildet. Der numerische Aufwand hierzu wäre sehr beträchtlich. Es müsste zum Beispiel eine erneute Vernetzung des Systems mit einem sogenannten adaptiven FE-Netz erfolgen. Aufgrund der genannten Einschränkungen können sich sehr große Verzerrungen im System aufbauen.
Bei sehr hoher Verzerrung sollte der Anwender manuell eine Teilung des Systems durchführen. Dies könnte beispielsweise über Kontaktvolumen mit entsprechenden analogen Fließgrenzen erfolgen. Weiterhin wird eine plastische Verzerrung des Elements über dieses Materialmodell nicht berücksichtigt. Dies kann besonders im Druckbereich hilfreich sein. Für das übliche Problem von gerissenem Beton im Zugbereich ist das Materialmodell ausreichend genau.
![Zależność kinematyczna między odniesieniem a bieżącą konfiguracją (źródło: [1])](/pl/webimage/009485/467007/02-de.png)