Nelineární materiálový model Poškození

Plochy tečení v programu RFEM (von Mises, Tresca, Drucker-Prager, Mohr-Coulomb)

Proto tato pravidla tečení umožňují modelovat jen čistě pružno-plastické chování. Pro materiály, které podléhají procesu poškození například vlivem trhlin, je vhodnější materiálový model Poškození. Dobrým příkladem takového materiálu je beton, který vykazuje podstatně vyšší pevnost v tlaku než v tahu. Trhliny, které vznikají v tahové oblasti materiálu, snižují tuhost konstrukce. U vyztuženého betonu nebo drátkobetonu přebírá tahová napětí v takovém případě výztuž.

Teoretické pozadí

Nelineární materiálové modely jsou obecně založeny na posunu tělesa v aktuálním přetvořeném prostoru do referenční konfigurace bez napětí (viz obr. 02). Podrobnější informace na toto téma naleznete například v [2].

Kinematický vztah mezi referenční a aktuální konfigurací (zdroj: [1])

Tenzor přetvoření udává deformace lokálního prvku v referenčním systému. Přetvoření v nedeformovaném referenčním systému se přitom odvozuje z Green-Langrandeova tenzoru přetvoření E = ½ ∙ (F^T ∙ F - 1) a přetvoření v lokálním souřadném systému z Euler-Almasiho tenzoru přetvoření e = ½ ∙ (I - b^-1). Dílčí integrací se z obou přetvoření vyvodí lineární deformace ε = ½ ∙ (H + H^T), z které lze při zohlednění Cauchyho teorému a Piola-Kirchhoffova tenzoru napětí vypočítat nominální napětí na tělese. Pomocí bilančních rovnic kontinua tak můžeme vyjádřit míru volné energie.

Bilanční rovnice kontinua:

• Bilance hmotnosti nám říká, že hmotnost systému zůstává stejná i při přetvoření.
  
  $$\mathrm{m} = {\int }_{\mathrm{Bt}}\mathrm{\rho d\nu } (\mathrm{verformtes} S\mathrm{ystem}) = {\int }_{\mathrm{B}0}\mathrm{dV} \left(\mathrm{Referenzsystem}\right) = \mathrm{konstant}$$

  Vzorec 1
• Bilance hybnosti jako časová změna celkové hybnosti
  
  $$\frac{\mathrm{d}}{\mathrm{dt}}{\int }_{\mathrm{Bt}}\mathrm{\rho ẋd\nu } = {\int }_{\mathrm{Bt}}\mathrm{\rho bd\nu } \left(\mathrm{Volumenkräfte}\right) {\int }_{\mathrm{\delta Bt}}\mathrm{tda} \left(\mathrm{Oberflächenkräfte}\right)$$

  Vzorec 2
• Bilance momentu hybnosti jako změna rychlosti celkové hybnosti
  
  $$\frac{\mathrm{d}}{\mathrm{dt}} {\int }_{\mathrm{Bt}}\mathrm{\rho x} · \mathrm{ẋd\nu } = {\int }_{\mathrm{Bt}}\mathrm{\rho } (\mathrm{x} · \mathrm{b}) \mathrm{d\nu } {\int }_{\mathrm{\delta Bt}}\mathrm{x} · \mathrm{td}$$

  Vzorec 3
• 1. termodynamický zákon: celková energie tělesa zůstává zachována.
  
  $$\frac{\mathrm{d}}{\mathrm{dt}}{\int }_{\mathrm{Bt}}(\mathrm{u} \frac{1}{2} · \mathrm{ẋ} · \mathrm{ẋ}) \mathrm{\rho d\nu } = {\int }_{\mathrm{Bt}}\mathrm{\rho r} \mathrm{b} · \mathrm{ẋd\nu } {\int }_{\mathrm{\delta Bt}}\mathrm{t} · \mathrm{ẋ} - \mathrm{q} · \mathrm{nda}$$

  Vzorec 4
  
  kinetická energie = mechanický výkon + povrchové napětí
• Druhý Hauptsatz der Thermodynamik: Beim Übergang in eine andere Ebene wird Energie (Wärme) frei.
  
  $$\frac{\mathrm{d}}{\mathrm{dt}}{\int }_{\mathrm{Bt}}\mathrm{\rho sd\nu } \ge {\int }_{\mathrm{Bt}}\mathrm{\rho } \frac{\mathrm{r}}{\mathrm{\theta }} \mathrm{\nu } - {\int }_{\mathrm{\delta Bt}}\frac{1}{\mathrm{\theta }} \mathrm{q} · \mathrm{nda}$$

  Vzorec 5

Stavové rovnice (konstituční rovnice) popisují materiálový vztah mezi tělesy. Vnitřními proměnnými (volná energie ψ, měrná entropie s, Cauchyho tenzor napětí σ, vektor tepelného toku q) se zohledňuje poškození v materiálovém modelu. V této souvislosti hraje důležitou úlohu také „paměť“ materiálu, tedy jeho časově závislé chování. Zohledňuje se kinematickým a izotropním zpevněním. S ohledem na poškození materiálu se složka deformace rozloží na pružnou a plastickou složku. Plastická složka se dále rozdělí na kinematickou a izotropní složku.
ε = ε^e + ε^p → ε^p = ε^iso + ε^kin

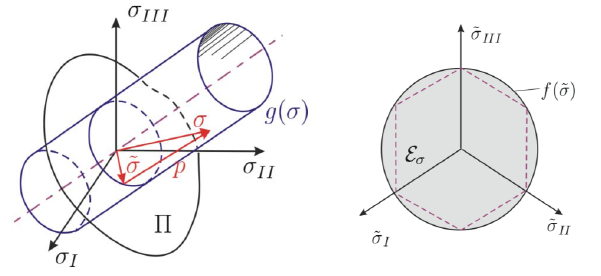
V příspěvku o nelineárním elastickém materiálovém chování jsme již uvedli, že funkce plasticity pro zohlednění účinků poškození závisí na neměnnosti tenzoru napětí. Konkrétně funkce plasticity podléhá omezující Kuhn-Tuckerově podmínce, která říká, že veškeré napěťové stavy v prostoru hlavních napětí jsou menší než 0, a tudíž jsou pružné. Napětí vně tohoto prostoru jsou nepřípustná a promítají se zpět na plochu plasticity v opravném kroku (predikční a korekční krok). Tento výpočet probíhá jako zkušební funkce, což vyžaduje nelineární Newton-Raphsonovu metodu výpočtu.

Grafische Darstellung der Fließfläche im Hauptspannungsraum

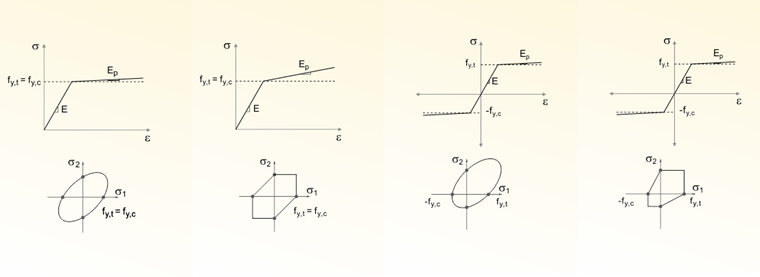
Funkce plasticity (z [4]) v materiálovém modelu Poškození rozlišuje mezi namáháním materiálu v tahu a namáháním v tlaku:

Přitom r představuje míru energie a h je zpevnění. Proměnné A a B vyjadřují poškození materiálu. Uplatňuje se přitom také podobně jako v následující kapitole pracovní diagram v prostoru hlavních napětí.

Poškození v programu RFEM

Po základním úvodu do problematiky se nyní budeme zabývat materiálovým modelem v programu RFEM. V našem příspěvku bylo možné poskytnout pouze rámcový vhled do tématu, a do jisté míry tak mohou chybět souvislosti. Doporučujeme proto podrobnější literaturu jako např. [2].

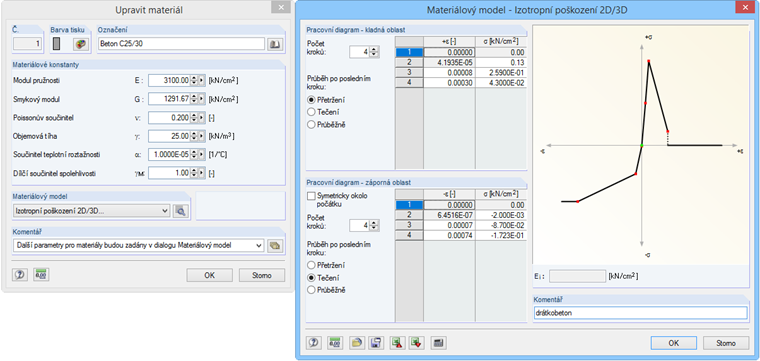
Vzhledem k nelineární metodě výpočtu s opravným krokem je třeba provést v první úrovni diagramu lineárně pružný výpočet. Při řešení v programu RFEM přitom přetvoření v druhé úrovni diagramu závisí na modulu pružnosti, který byl stanoven v dialogu pro zadání materiálu, a dále na definovaném mezním napětí (viz obr. 04).

Eingabe der Spannungs-Dehnungs-Beziehung in RFEM

Pro přetvoření přitom platí Hookův zákon ε = σ/E. Po tomto prvním pružném predikčním kroku lze přistoupit k téměř libovolnému nesymetrickému zadání pracovního diagramu. Modul pružnosti materiálu přitom může být také záporný, neboť se zpětně stanoví z následujícího vztahu:

Protože je ovšem modul pružnosti zapotřebí pouze pro zpětný výpočet, připouští se tu také absolutní hodnota modulu. Výpočet s opravnou iterací vede u materiálového modelu Poškození k tomu, že tuhost systému se tak dlouho snižuje, až se nepřenáší žádné napětí v žádném prvku sítě KP. Přetvoření v prvku přitom mohou být značně velká.

Závěr

Materiálový model Poškození umožňuje nelineární výpočet s nesymetrickými, téměř libovolnými vztahy mezi napětím a přetvořením. I při poškození materiálu zůstává systém ale nadále kontinuem. To znamená, že v systému nevznikají trhliny. Numerická náročnost by ovšem byla v tomto případě značná. Například by bylo zapotřebí nové zesíťování systému s takzvanou adaptivní sítí konečných prvků. V důsledku uvedených omezení může docházet k velkým přetvořením v systému.

V případě výrazného přetvoření by měl uživatel systém rozdělit. Může k tomu například použít kontaktní tělesa s odpovídající podobnou mezí kluzu. Dále se plastické přetvoření prvku při použití tohoto materiálového modelu nezohledňuje, což může být zvlášť v tlačené oblasti výhodné. Pro řešení běžného problému, jímž je beton poškozený trhlinami v tažené oblasti, je tento materiálový model dostatečně přesný.

Reference