Usando o RFEM, você tem a capacidade de analisar vários componentes estruturais, como elementos de membro, placas, paredes, cascas e sólidos. Antes de realizar qualquer cálculo, é necessário gerar uma malha de elementos finitos (EF) que corresponda aos elementos desejados 1D, 2D e 3D.
A análise EF envolve a divisão do sistema estrutural em subsistemas menores, cada um representado por elementos finitos. As condições de equilíbrio são estabelecidas para cada um desses elementos. Esse processo leva à formulação de um sistema linear de equações com inúmeras variáveis desconhecidas. A precisão dos resultados é diretamente influenciada pelo nível de refinamento no tamanho da malha dos elementos finitos. É importante notar que uma malha mais fina melhora a precisão, mas também aumenta significativamente o tempo de computação devido à maior quantidade de dados sendo processados. Isso ocorre porque equações adicionais precisam ser resolvidas para cada nó EF suplementar.
Felizmente, a malha EF é gerada automaticamente pelo software. No entanto, existem opções que fornecem controle sobre o processo de geração da malha.
Elementos 1D
Em relação aos elementos de membro, assume-se que a seção transversal mantém sua forma plana durante a deformação. Elementos de membro 1D são empregados para representar vigas, trusses, nervuras, cabos e conexões rígidas. Cada elemento de membro 1D abrange um total de doze graus de liberdade – seis em seu ponto de início e seis em seu ponto final. Esses graus de liberdade dizem respeito a deslocamentos (ux, uy, uz) e rotações (φx, φy, φz).
Se o complemento de empolamento de torção estiver ativado, um grau de liberdade adicional está disponível em cada nó, que pode ser usado para considerar o empolamento.
No contexto da análise estrutural linear, a tensão, compressão e torção são expressas como funções lineares ao longo do eixo do membro (x), independentemente dos efeitos de flexão e cisalhamento. Esta representação aproxima esses efeitos usando um polinômio de terceira ordem em x, que também considera a influência de tensões de cisalhamento resultantes das forças de cisalhamento Vy e Vz. A matriz de rigidez KL(12, 12) caracteriza o comportamento linear desses elementos 1D. Além disso, para cenários envolvendo problemas geometricamente não lineares onde a força axial interage com a flexão, a matriz de rigidez KNL(12, 12) é empregada.
Para cálculos precisos em casos envolvendo deformações significativas, é aconselhável melhorar a precisão da malha de elementos finitos (EF) para linhas, conforme detalhado no Capítulo Line Mesh Refinements da documentação.
Elementos 2D
Comumente, elementos quadrilaterais servem como componentes 2D na análise estrutural. O processo de geração da malha introduz elementos triangulares onde eles são necessários. Os graus de liberdade associados aos nós de canto de ambos os elementos quadrilaterais e triangulares alinham-se com os dos elementos 1D, abrangendo deslocamento (ux, uy, uz) e rotação (φx, φy, φz). Este arranjo assegura compatibilidade entre elementos 1D e 2D nos nós. Os parâmetros são inicialmente definidos no sistema de coordenadas planares locais dos elementos e posteriormente transformados para o sistema de coordenadas globais durante a criação da matriz de rigidez global.
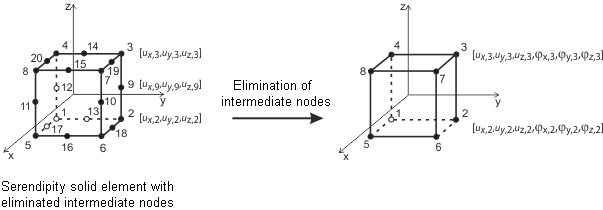
Os elementos de casca plana são baseados na teoria de Mindlin/Reissner. A representação gráfica na figura ilustra as abordagens dos elementos. Para conectar diretamente com elementos de membro, é adotada uma abordagem quadrada no plano da casca (ux, uy). Esta escolha elimina nós intermediários, resultando em um elemento de quatro nós com um grau de liberdade adicional φx. Esta configuração facilita o acoplamento direto entre elementos de parede e elementos de viga. Além disso, são empregados elementos MITC4 (Mixed Interpolation of Tensorial Components) conforme introduzido por Dvorkin e Bathe [1]. Eles baseiam-se em uma técnica de interpolação mista que abrange deformações transversais, rotações de seção transversal e deformações de cisalhamento transversal.
Atualmente, os elementos de membro são tratados resolvendo a equação diferencial de análise de segunda ordem diretamente. No entanto, ao usar a torção de Saint Venant, os efeitos de empolamento não são considerados. A análise de membranas é baseada nos princípios de Bergan. Por exemplo, elementos triangulares são definidos dividindo as funções fundamentais em três deformações de corpo rígido, três condições de deformação constante e três gradientes lineares específicos de tensão e deformação. Dentro de um elemento, o campo de deformação exibe comportamento quadrático, enquanto o campo de tensão mantém linearidade. A matriz de rigidez do elemento KL é então transformada em nove parâmetros combinados dos tipos ux, uy, φz. Esses componentes da matriz são incorporados na matriz de rigidez geral (18, 18), juntamente com os componentes que contribuem para os efeitos de flexão e cisalhamento, resultando no conceito Lynn/Dhillon.
Subsequentemente, a análise envolve a aplicação de placas de Mindlin, onde placas com distorções de cisalhamento distintivas são analisadas usando os princípios de Timoshenko. Isso permite que o RFEM resolva corretamente problemas relacionados a placas grossas e finas (placas de Navier). Em casos de questões geometricamente não lineares, a divisão das condições de tensão-deformação em um estado planar e em flexão com interações de cisalhamento não é viável. As interações entre esses estados são consideradas através da matriz KNL. O RFEM utiliza uma versão simplificada, mas eficaz, da matriz KNL, influenciada pelas abordagens de Zienkiewicz. O componente quadrado ε2 do tensor de deformação de Green/Lagrange ε = ε1 + ε2 é empregado. Assume-se uma distribuição linear de uz(x, y) sob a condição de tensão planar e distribuições lineares de ux(x, y) e uy(x, y) durante a interação de flexão. Esta suposição é válida devido ao impacto principal da interação depender da primeira derivada da equação diferencial e à rápida redução na influência dos componentes de ordem superior com subdivisões menores do elemento. Numerosas análises numéricas validaram a correção dessa abordagem.
Ao lidar com elementos de casca, é essencial que a espessura dos elementos seja significativamente menor que sua extensão. Se esta condição não for atendida, é aconselhável modelar objetos como sólidos. Além disso, ao utilizar elementos de casca, deve-se exercer uma introdução gradual de tensões de torção, já que o grau de liberdade rotacional em torno da normal da superfície é altamente sensível.
Elementos 3D
Os seguintes elementos 3D estão implementados no RFEM: tetraedro, pentaedro (prisma, pirâmide) e hexaedro. Informações detalhadas sobre elementos aplicados e matrizes podem ser encontradas em Sevčík 3D Finite Elements with Rotational Degrees of Freedom (em tcheco, disponível na Dlubal Software mediante solicitação).
Geralmente, todos os graus de liberdade rotacionais devem ser considerados críticos para sólidos. Como a deformação de um sólido é determinada unicamente a partir dos vetores de deslocamento, a rotação de um nó da malha, por exemplo, devido à torsão singularmente introduzida, não afeta a deformação dentro do sólido.