Elementy skończone z punktu widzenia topologii

Korzystając z RFEM, masz możliwość analizy różnych elementów konstrukcyjnych, takich jak belki, płyty, ściany, powłoki i bryły. Przed przystąpieniem do jakichkolwiek obliczeń konieczne jest wygenerowanie siatki elementów skończonych (FE), która odpowiada pożądanym elementom 1D, 2D i 3D.

Analiza FE polega na podziale systemu konstrukcyjnego na mniejsze podsystemy, z których każdy jest reprezentowany przez elementy skończone. Dla każdego z tych elementów ustalane są warunki równowagi. Proces ten prowadzi do sformułowania układu równań liniowych z licznymi niewiadomymi. Dokładność wyników jest bezpośrednio uwarunkowana poziomem dokładności rozmiaru siatki elementów skończonych. Warto zauważyć, że drobniejsza siatka zwiększa dokładność, ale również znacznie wydłuża czas obliczeń z powodu większej ilości przetwarzanych danych. Dzieje się tak, ponieważ dla każdego dodatkowego węzła FE należy rozwiązać dodatkowe równania.

Na szczęście siatka FE jest generowana automatycznie przez oprogramowanie. Niemniej jednak istnieją opcje umożliwiające kontrolę nad procesem generacji siatki.

Elementy 1D

W odniesieniu do elementów prętowych zakłada się, że przekrój zachowuje swój płaski kształt podczas deformacji. Elementy prętowe 1D są używane do reprezentowania belek, kratownic, żeber, kabli i połączeń sztywnych. Każdy element prętowy 1D obejmuje łącznie dwanaście stopni swobody – sześć na swoim początku i sześć na jego końcu. Te stopnie swobody odnoszą się do przemieszczeń (u_x, u_y, u_z) i obrotów (φ_x, φ_y, φ_z).

Jeśli dodatek do skręcania wyboistego jest aktywowany, dodatkowy stopień swobody jest dostępny w każdym węźle, co pozwala uwzględnić wyboistość.

W kontekście liniowej analizy strukturalnej, rozciąganie, ściskanie i skręcanie są wyrażone jako funkcje liniowe wzdłuż osi pręta (x), niezależnie od efektów zginania i ścinania. Reprezentacja ta aproksymuje te efekty za pomocą wielomianu trzeciego stopnia w x, który także uwzględnia wpływ naprężeń ścinających wynikających z sił tnących V_y i V_z. Macierz sztywności K_L(12, 12) charakteryzuje liniowe zachowanie tych elementów 1D. Dodatkowo, dla scenariuszy z udziałem problemów geometrycznie nieliniowych, gdzie siła osiowa współdziała ze zginaniem, stosowana jest macierz sztywności K_NL(12, 12).

Dla dokładnych obliczeń w przypadkach znaczących deformacji zaleca się zwiększenie precyzji siatki elementów skończonych (FE) dla linii, jak opisano w rozdziale Linia Siatki Udokładniającej dokumentacji.

Elementy 2D

Zazwyczaj, elementy czworokątne służą jako komponenty 2D w analizie strukturalnej. Proces generowania siatki wprowadza elementy trójkątne tam, gdzie są potrzebne. Stopnie swobody związane z węzłami narożnymi zarówno elementów czworokątnych, jak i trójkątnych, są zgodne z tymi dla elementów 1D, obejmując przemieszczenia (u_x, u_y, u_z) i obroty (φ_x, φ_y, φ_z). Takie ułożenie zapewnia kompatybilność między elementami 1D i 2D na węzłach. Parametry są początkowo definiowane w lokalnym układzie współrzędnych płaskich elementów, a następnie przekształcane na globalny układ współrzędnych podczas tworzenia globalnej macierzy sztywności.

Elementy powłokowe (2D) w RFEM

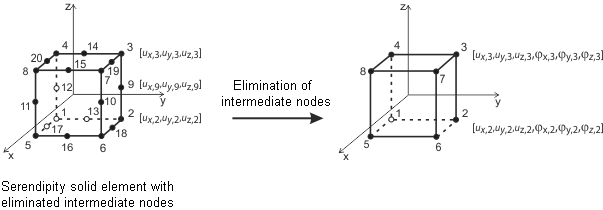
Płaskie elementy powłokowe opierają się na teorii Mindlina/Reissnera. Graficzne przedstawienie na rysunku ilustruje podejście elementarne. Do bezpośredniego połączenia z elementami prętowymi przyjęto podejście kwadratowe w płaszczyźnie powłoki (u_x, u_y). Ten wybór eliminuje węzły pośrednie, skutkując elementem czterowęzłowym z dodatkowym stopniem swobody φ_x. Konfiguracja ta ułatwia bezpośrednie sprzężenie między elementami ścian i elementami belek. Dodatkowo stosowane są elementy MITC4 (Mixed Interpolation of Tensorial Components) wprowadzone przez Dvorkina i Bathe`a [1]. Opierają się one na mieszanej technice interpolacji obejmującej deformacje poprzeczne, obroty przekroju oraz odkształcenia poprzeczne.

Obecnie elementy prętowe są traktowane poprzez bezpośrednie rozwiązanie równania różniczkowego analizy drugiego rzędu. Jednakże, przy stosowaniu skręcania Saint Venanta, efekty wyboistości nie są uwzględniane. Analiza membran oparta jest na zasadach Bergana. Na przykład, elementy trójkątne definiowane są przez podział podstawowych funkcji na trzy deformacje ciała sztywnego, trzy stanów naprężeń stałych i trzy określone gradienty liniowe naprężeń i odkształceń. W obrębie elementu pole deformacji wykazuje zachowanie kwadratowe, podczas gdy pole naprężeń zachowuje liniowość. Macierz sztywności elementu K_L jest następnie przekształcana w dziewięć połączonych parametrów typów u_x, u_y, φ_z. Komponenty tej macierzy są zintegrowane z całą macierzą sztywności (18, 18), wraz z komponentami przyczyniającymi się do efektów zginania i ścinania, co daje koncepcję Lynna/Dhillona.

Kolejno, analiza obejmuje zastosowanie płyt Mindlina, w których analizowane są płytki z charakterystycznymi zniekształceniami ścinającymi przy użyciu zasad Timoszenki. Pozwala to RFEM na poprawne rozwiązanie problemów zarówno z grubymi, jak i cienkimi płytami (płytami Naviera). W przypadku problemów geometrycznie nieliniowych nie jest możliwe podzielenie warunków naprężeniowo-odkształceniowych na stan płaski i zginanie z interakcjami rywalizującymi z siłami ścinającymi. Interakcje między tymi stanami są uwzględniane przez macierz K_NL. RFEM wykorzystuje uproszczoną, lecz skuteczną wersję macierzy K_NL, wpływającą na podejścia Zienkiewicza. Używana jest kwadratowa komponenta ε₂ tensora odkształceń Green/Lagrange ε = ε₁ + ε₂. Zakłada się liniową dystrybucję u_z(x, y) w warunku naprężeniowym płaskim i liniowe dystrybucje u_x(x, y) oraz u_y(x, y) w interakcji podczas zginania. Przyjęcie to jest uzasadnione, ponieważ główny wpływ interakcji zależy od pierwszej pochodnej równania różniczkowego oraz szybkiego spadku wpływu składników wyższego rzędu z mniejszymi podziałami elementów. Liczne analizy numeryczne potwierdziły poprawność tego podejścia.

W przypadku elementów powłokowych istotne jest, aby grubość elementów była znacznie mniejsza niż ich rozciąganie. Jeśli ten warunek nie jest spełniony, zaleca się modelowanie obiektów jako brył. Ponadto, korzystając z elementów powłokowych, należy stopniowo wprowadzać naprężenia skrętne, ponieważ stopień swobody obrotu wokół normalne do powierzchni jest bardzo wrażliwy.

Elementy 3D

Następujące elementy 3D są zaimplementowane w RFEM: czworościan, pięciokształt (graniastosłup, ostrosłup) i sześcian. Szczegółowe informacje o stosowanych elementach i macierzach można znaleźć w pracy 3D Finite Elements with Rotational Degrees of Freedom Sevčíka (w języku czeskim, dostępna na żądanie od Dlubal Software).

Element bryłowy (sześcian)

Ogólnie rzecz biorąc, wszystkie obrotowe stopnie swobody trzeba traktować jako krytyczne dla brył. Ponieważ deformacja bryły jest określona wyłącznie na podstawie wektorów przemieszczenia, obrót węzła siatki, na przykład spowodowany wprowadzeniem skręcania, nie wpływa na deformację wewnątrz bryły.