En utilisant RFEM, vous avez la capacité d'analyser divers composants structurels tels que des éléments de barre, des plaques, des murs, des coques et des solides. Avant d'effectuer des calculs, il est nécessaire de générer un maillage d'éléments finis (EF) qui correspond aux éléments 1D, 2D et 3D souhaités.
L'analyse EF implique de décomposer le système structurel en sous-systèmes plus petits, chacun étant représenté par des éléments finis. Des conditions d'équilibre sont établies pour chacun de ces éléments. Ce processus conduit à la formulation d'un système d'équations linéaires avec de nombreuses variables inconnues. La précision des résultats est directement influencée par le niveau de raffinement de la taille du maillage des éléments finis. Il est important de noter qu'un maillage plus fin améliore l'exactitude, mais il augmente également considérablement le temps de calcul en raison de la quantité plus importante de données à traiter. Cela s'explique par le fait que des équations supplémentaires doivent être résolues pour chaque nœud EF supplémentaire.
Heureusement, le maillage EF est généré automatiquement par le logiciel. Néanmoins, des options existent pour contrôler le processus de génération de maillage.
Éléments 1D
En ce qui concerne les éléments de barre, on suppose que la section transversale conserve sa forme plane lors de la déformation. Les éléments de barre 1D sont employés pour représenter les poutres, treillis, nervures, câbles et connexions rigides. Chaque élément de barre 1D englobe un total de douze degrés de liberté - six à son point de départ et six à son point terminal. Ces degrés de liberté concernent les déplacements (ux, uy, uz) et les rotations (φx, φy, φz).
Si l'add-on de gauchissement en torsion est activé, un degré de liberté supplémentaire est disponible à chaque nœud, qui peut être utilisé pour prendre en compte le gauchissement.
Dans le contexte de l'analyse structurelle linéaire, la tension, la compression et la torsion sont exprimées en tant que fonctions linéaires le long de l'axe de la barre (x), indépendamment des effets de flexion et de cisaillement. Cette représentation approxime ces effets en utilisant un polynôme de troisième ordre en x, qui tient également compte de l'influence des contraintes de cisaillement résultant des efforts tranchants Vy et Vz. La matrice de rigidité KL(12, 12) caractérise le comportement linéaire de ces éléments 1D. De plus, pour les scénarios impliquant des problèmes géométriquement non linéaires où la force axiale interagit avec la flexion, la matrice de rigidité KNL(12, 12) est utilisée.
Pour des calculs précis dans les cas impliquant des déformations significatives, il est conseillé d'améliorer l'exactitude du maillage d'éléments finis (EF) pour les lignes, comme détaillé dans le Chapitre Line Mesh Refinements de la documentation.
Éléments 2D
Couramment, les éléments quadrilatéraux servent de composants 2D dans l'analyse structurelle. Le processus de génération de maillage introduit des éléments triangulaires là où ils sont nécessaires. Les degrés de liberté associés aux nœuds de coin des éléments quadrilatéraux et triangulaires s'alignent avec ceux des éléments 1D, englobant les déplacements (ux, uy, uz) et les rotations (φx, φy, φz). Cet agencement assure la compatibilité entre les éléments 1D et 2D au niveau des nœuds. Les paramètres sont d'abord définis dans le système de coordonnées plan local des éléments et ensuite transformés dans le système de coordonnées global lors de la création de la matrice de rigidité globale.
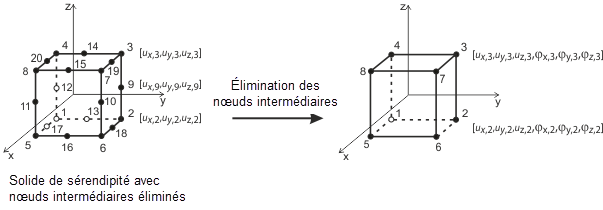
Les éléments de coque plane sont fondés sur la théorie de Mindlin/Reissner. La représentation graphique dans la figure illustre les approches élémentaires. Pour établir un lien direct avec les éléments de barre, une approche carrée est adoptée dans le plan de la coque (ux, uy). Ce choix élimine les nœuds intermédiaires, aboutissant à un élément à quatre nœuds avec un degré de liberté supplémentaire φx. Cette configuration facilite le couplage direct entre les éléments de mur et de poutre. De plus, les éléments MITC4 (Mixed Interpolation of Tensorial Components) tels qu'introduits par Dvorkin et Bathe [1] sont employés. Ils reposent sur une technique d'interpolation mixte englobant les déformations transversales, les rotations de la section et les déformations de cisaillement transversal.
Actuellement, les éléments de barre sont traités en résolvant directement l'équation différentielle d'analyse du second ordre. Cependant, lors de l'utilisation de la torsion de Saint Venant, les effets de gauchissement ne sont pas pris en compte. L'analyse des membranes est basée sur les principes de Bergan. Par exemple, les éléments triangulaires sont définis en décomposant les fonctions fondamentales en trois déformations de corps rigide, trois conditions de déformation constante et trois gradients linéaires spécifiques de contrainte et de déformation. Au sein d'un élément, le champ de déformation montre un comportement quadratique, tandis que le champ de contrainte maintient la linéarité. La matrice de rigidité de l'élément KL est ensuite transformée en neuf paramètres combinés des types ux, uy, φz. Ces composants matriciels sont incorporés dans la matrice de rigidité globale (18, 18), aux côtés des composants contribuant aux effets de flexion et de cisaillement, résultant dans le concept Lynn/Dhillon.
Par la suite, l'analyse implique l'application de plaques de Mindlin, dans laquelle les plaques avec des distortions de cisaillement distinctives sont analysées en utilisant les principes de Timoshenko. Cela permet à RFEM de résoudre correctement les problèmes liés aux plaques épaisses et minces (plaques de Navier). En cas de problèmes géométriquement non linéaires, la division des conditions de contrainte-déformation en un état plan et une interaction de flexion avec cisaillement n'est pas réalisable. Les interactions entre ces états sont prises en compte par la matrice KNL. RFEM utilise une version simplifiée mais efficace de la matrice KNL, influencée par les approches de Zienkiewicz. La composante carrée ε2 du tenseur de déformation Green/Lagrange ε = ε1 + ε2 est employée. Une distribution linéaire de uz(x, y) sous la condition de contrainte plane et des distributions linéaires de ux(x, y) et uy(x, y) lors de l'interaction de flexion sont supposées. Cette supposition est valide en raison de l'impact principal de l'interaction étant dépendant de la première dérivée de l'équation différentielle et de la réduction rapide de l'influence des composants de plus haute ordre avec des divisions d'éléments plus petites. De nombreuses analyses numériques ont validé la justesse de cette approche.
Lors du traitement des éléments de coque, il est essentiel que l'épaisseur des éléments soit significativement plus petite que leur extension. Si cette condition n'est pas remplie, il est conseillé de modéliser les objets en tant que solides. De plus, lors de l'utilisation d'éléments de coque, une introduction progressive des contraintes de torsion doit être exercée, la rotation autour de la normale à la surface étant très sensible.
Éléments 3D
Les éléments 3D suivants sont implémentés dans RFEM : tétraèdre, pentaèdre (prisme, pyramide) et hexaèdre. Des informations détaillées sur les éléments appliqués et les matrices peuvent être trouvées dans Sevčík 3D Finite Elements with Rotational Degrees of Freedom (en tchèque, disponible auprès de Dlubal Software sur demande).
Généralement, tous les degrés de liberté de rotation doivent être considérés comme critiques pour les solides. Comme la déformation d'un solide est uniquement déterminée à partir des vecteurs de déplacement, la rotation d'un nœud de maillage, par exemple en raison d'une torsion introduite de manière singulière, n'affecte pas la déformation à l'intérieur du solide.