有限元分析软件（例如 RFEM）可以在计算内力时对结构构件进行加劲肋设计。 Das Gebäude kann darin mit allen tragenden Gebäudeteilen, Öffnungen und so weiter abgebildet und als Gesamtmodell berechnet werden.
Die Vordimensionierung von Aussteifungssystemen kann mit den in [1] dargestellten Berechnungsverfahren mittels Handrechnung oder unter Verwendung von Programmen wie DUENQ erfolgen. Sie eröffnen dem Ingenieur ein besseres Verständnis für den Lastabtrag des Systems sowie den Tragfähigkeitsbeitrag der einzelnen Bauteile.
Verteilung der Horizontalkräfte
Die Horizontallastverteilung für Biege- oder Torsionsbeanspruchung auf die aussteifenden Bauteile kann gemäß den nachfolgenden Formeln berechnet werden.
Forces due to Bending
值:
Vy,i, Vz,i: Querkraft in y- beziehungsweise z-Richtung, die den Teilquerschnitt i belastet
Vy, Vz: Querkraft in y- beziehungsweise z-Richtung, die den Gesamtquerschnitt belastet
Iy,i, Iz,i, Iyz,i: Trägheitsmomente des Teilquerschnitts i, bezogen auf die zu Y und Z parallelen Achsen durch den Teilquerschnitts-Schwerpunkt Si
Iy, Iz: Gesamtträgheitsmomente bezogen auf den Gesamtschwerpunkt S
Forces due to Torsion
值:
Vy,i, Vz,i: Querkraft in y- beziehungsweise z-Richtung, die den Teilquerschnitt i belastet
Mxs: sekundäres Torsionsmoment, das den Gesamtquerschnitt belastet
Iy,i, Iz,i, Iyz,i: Trägheitsmomente des Teilquerschnitts i, bezogen auf die zu Y und Z parallelen Achsen durch den Teilquerschnitts-Schwerpunkt Si
Iω,i: Wölbwiderstand bezogen auf den Teilquerschnitts-Schubmittelpunkt Mi
yM,i, zM,i: Koordinate des Teilquerschnitts-Schubmittelpunkts Mi
yM, zM: Koordinate des Gesamtschubmittelpunktes M
示例
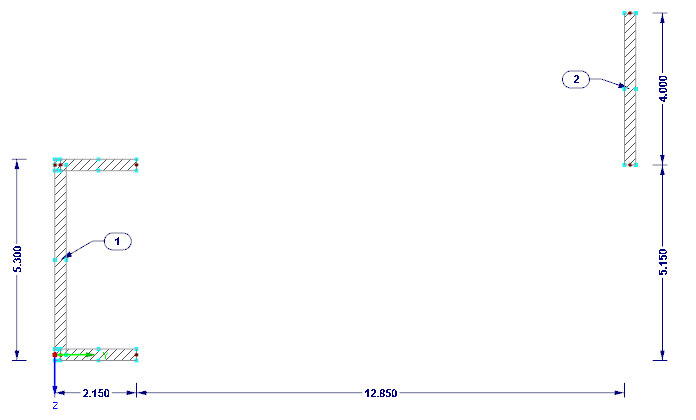
Die Verteilung der horizontalen Lasten auf die aussteifenden Elemente soll an dem im Bild 1 dargestellten System exemplarisch ermittelt werden.
Wandstärke t = 30 cm
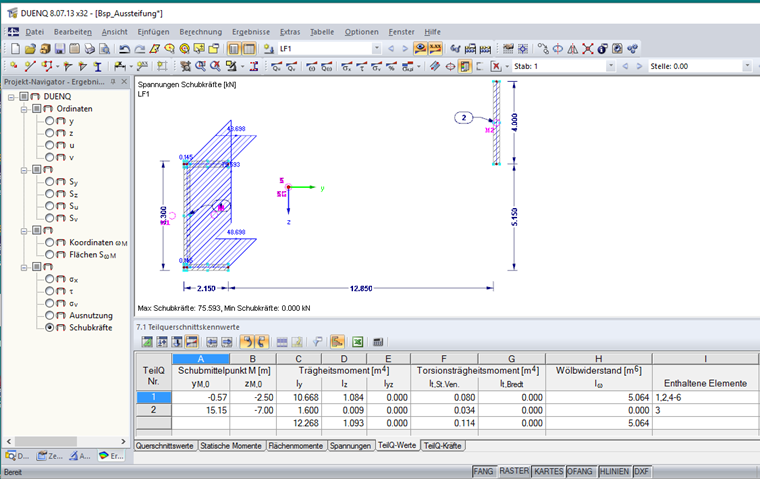
截面属性
Teilquerschnitt 1
Teilquerschnitt 2
Gesamtquerschnitt
Iy = 10,668 + 1,600 = 12,268 m4
Iz = 1,084 + 0,009 = 1,093 m4
Die mit DUENQ 8 ermittelten Querschnittskennwerte sind im Bild 2 dargestellt.
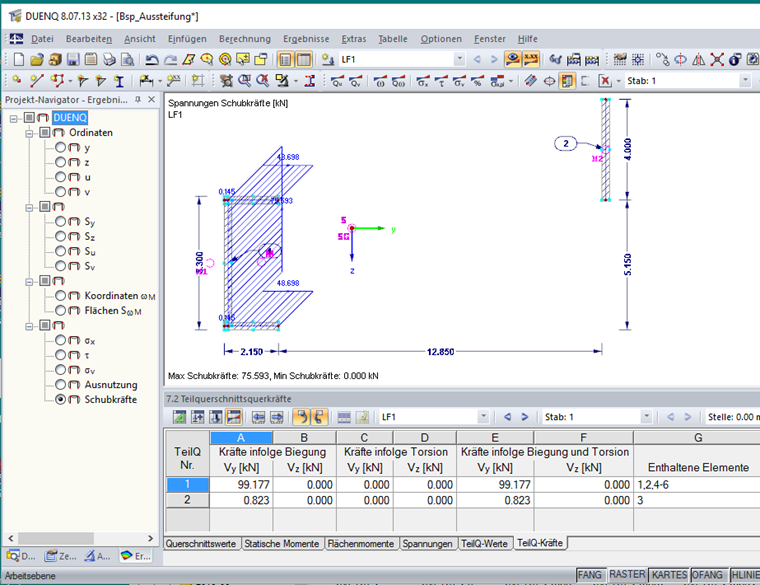
截面组成部分的内力
Die mit DUENQ 8 ermittelten Teilquerschnittsquerkräfte sind im Bild 3 dargestellt.
参考
[1] Beck, H.; Schäfer, H.: Die Berechnung von Hochhäusern durch Zusammenfassung aller aussteifenden Bauteile zu einem Balken. Der Bauingenieur, Heft 3, 1969
.png?mw=350&hash=83397b9718189d605563213de7c48c3b3b18b064)
