4998x

001431

Sonja von Bloh, M.Sc.

1.5.2017

Vyztužení nosných konstrukcí

Konstrukce je třeba navrhnout a propracovat tak, aby se svislá i vodorovná zatížení bezpečně a bez přílišných deformací přenášela do podloží. Vodorovná zatížení představuje například vítr, nežádoucí naklonění, zemětřesení nebo náraz.

Pro výpočet vnitřních sil a návrh výztužných konstrukčních prvků můžeme použít programy založené na metodě konečných prvků, jako je RFEM. Budovu v nich lze modelovat se všemi nosnými konstrukčními dílci, otvory a ostatními prvky a celý model pak lze podrobit výpočtům.

Při předběžném návrhu výztužných systémů můžeme vycházet z ručního výpočtu, který lze provést metodou popsanou v [1], anebo můžeme využít programy jako SHAPE‑THIN. Tyto programy poskytují uživatelům lepší přehled o přenosu zatížení konstrukce i o příspěvku jednotlivých konstrukčních částí na únosnosti systému.

Rozložení vodorovných sil

Rozdělení vodorovných sil na výztužné prvky při ohybovém a torzním namáhání lze stanovit pomocí následujících rovnic.

Síly od ohybu

Error converting from LaTeX to MathML

Vzorec 1

kde
V_y,i, V_z,i: posouvající síla ve směru y, resp. z, kterou je namáhán dílčí průřez i
V_y, V_z: posouvající síla ve směru y, resp. z, kterou je namáhán celý průřez
I_y,i, I_z,i, I_yz,i: momenty setrvačnosti dílčího půřezu i, vztažené k osám procházejícím těžištěm dílčího průřezu S_i a rovnoběžným s osami Y a Z
I_y, I_z: celkové momenty setrvačnosti vztažené k těžišti celého průřezu S

Síly od kroucení

Error converting from LaTeX to MathML

Vzorec 2

kde
V_y,i, V_z,i: posouvající síla ve směru y, resp. z, kterou je namáhán dílčí průřez i
M_xs: sekundární kroutící moment, kterým je namáhán celý průřez
I_y,i, I_z,i, I_yz,i: momenty setrvačnosti dílčího půřezu i, vztažené k osám procházejícím těžištěm dílčího průřezu S_i a rovnoběžným s osami Y a Z
I_ω,i je deplanační konstanta vztažená ke středu smyku M_i dílčího průřezu,
y_M,i, z_M,i: souřadnice středu smyku M_i dílčího průřezu
y_M, z_M: souřadnice středu smyku M celého průřezu

Příklad

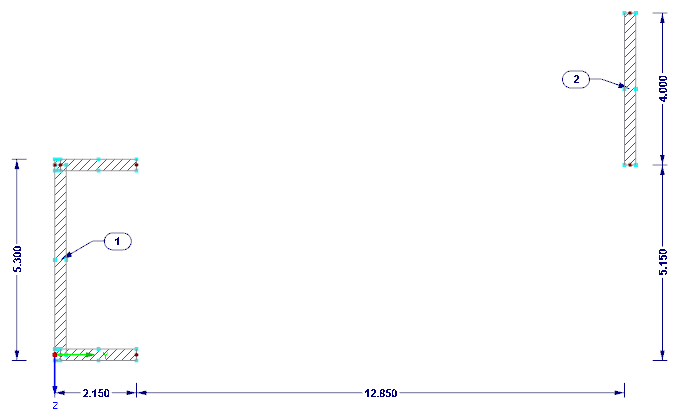
Výpočet rozložení vodorovných zatížení na výztužné prvky si názorně předvedeme na konstrukci, kterou vidíme na obr. 01.

Systém

Tloušťka stěny t = 30 cm

průřezové charakteristiky

Dílčí průřez 1

\begin{array}{l} z_{S, 1} = \frac{\frac{2.15 \cdot 0.30 \cdot 0.30}{2} + 4.70 \cdot 0.30 \cdot (\frac{4.70}{2} + 0.30) + 2.15 \cdot 0.30 \cdot (0.30 + 4.70 + \frac{0.30}{2})}{2.15 \cdot 0.30 \cdot 2 + 4.70 \cdot 0.30} = 2.65 m \\ y_{S, 1} = \frac{2.15 \cdot 0.30 \cdot \frac{2.15}{2} \cdot 2 + 4.70 \cdot 0.30 \cdot \frac{0.30}{2}}{2.15 \cdot 0.30 \cdot 2 + 4.70 \cdot 0.30} = 0.59 m \\ I_{y, 1} = 2.15 \cdot \frac{0.303}{12} \cdot 2 + 2.15 \cdot 0.30 \cdot (\frac{2.65 - 0.30}{2}) ² \cdot 2 + 0.30 \cdot \frac{4.703}{12} + 4.70 \cdot 0.30 \cdot (0.00) ² = 10.668 m^{4} \\ I_{z, 1} = 0.30 \cdot \frac{2.153}{12} \cdot 2 + 2.15 \cdot 0.30 \cdot (\frac{2.15}{2} - 0.59) ² \cdot 2 + 4.70 \cdot \frac{0.303}{12} + 4.70 \cdot 0.30 \cdot (0.59 - \frac{0.30}{2}) ² = 1.084 m^{4} \end{array}

Vzorec 3

Dílčí průřez 2

\begin{array}{l} I_{y, 2} = \frac{0, 30 \cdot 4, 003}{12} = 1, 600 m^{4} \\ I_{z, 2} = \frac{4, 00 \cdot 0, 303}{12} = 0, 009 m^{4} \end{array}

Vzorec 4: Dílčí průřez 2

Celý průřez
I_y = 10,668 + 1,600 = 12,268 m⁴
I_z = 1,084 + 0,009 = 1,093 m⁴

Průřezové hodnoty, které vypočítal program SHAPE-THIN, jsou znázorněny na obr. 02.

Průřezové charakteristiky

Posouvající síly v dílčím průřezu

\begin{array}{l} V_{y, 1} = \frac{100 \cdot (1, 084 \cdot 12, 268)}{12, 268 \cdot 1, 093} = 99, 18 kN \\ V_{y, 2} = \frac{100 \cdot (0, 009 \cdot 12, 268)}{12, 268 \cdot 1, 093} = 0, 823 kN \end{array}

Vzorec 5: Smykové síly dílčího průřezu

Posouvající síly v dílčím průřezu, které vypočítal program SHAPE‑THIN, vidíme na obr. 03.

Posouvající síly v dílčím průřezu

Reference

[1] Beck, H.; Schäfer, H.: Die Berechnung von Hochhäusern durch Zusammenfassung aller aussteifenden Bauteile zu einem Balken. Der Bauingenieur, Heft 3, 1969

Autor

Ing. von Bloh zajišťuje technickou podporu zákazníkům a je zodpovědná za vývoj programu RSECTION a addonů pro ocelové a hliníkové konstrukce.

Odkazy

Programy pro průřezové charakteristiky

Stahování

Model v programu SHAPE-THIN

376 KB

;