Contreventement des structures

Les programmes d'analyse par éléments finis tels que RFEM vous permettent de déterminer les efforts internes et de calculer les éléments structuraux de contreventement. Dans ce programme, vous pouvez modéliser un bâtiment avec tous les composants structuraux, ouvertures et autres éléments, et effectuer un calcul de l'ensemble du modèle.

Le prédimensionnement du système de contreventement peut être effectué à l'aide d'un calcul manuel selon la méthode de calcul décrite dans [1] ou à l'aide d'un programme tel que SHAPE-THIN. Ce logiciel permet aux ingénieurs de mieux comprendre le transfert de charge dans une structure et la contribution de la résistance de chaque composant.

Distribution des efforts horizontaux

La répartition horizontale des charges pour les efforts en flexion ou en torsion des éléments de contreventement peut être calculée à l'aide des formules suivantes.

Forces dues à la flexion

où
V_{y, i} , V_{z, i} : effort tranchant dans la direction y ou z, qui affecte la section partielle
V_y, V_z: effort tranchant dans la direction y ou z, qui affecte la section brute
I_y,i, I_z,i, I_yz,i: moments d'inertie de la section partielle i relatifs aux axes parallèles Y et Z du centre de gravité de section partielle S_i
I_y, I_z: Moments total d'inertie liés au centre de gravité global S

Forces dues à la torsion

où
V_{y, i} , V_{z, i} : effort tranchant dans la direction y ou z, qui affecte la section partielle
M_xs : moment de torsion secondaire, qui affecte la section brute
I_{y, i} , I_{z, i} , I_{yz, i} : moments d'inertie de la section partielle i relatifs aux axes parallèles Y et Z du centre de gravité de section partiel S_i
I_ω,i est la constante de gauchissement rapportée au centre de cisaillement M_i de la section partielle,
y_{M, i} , z_{M, i} : coordonnée du centre de cisaillement de la section partielle M_i
y_M , z_M : coordonnée du centre global de cisaillement M

Exemple

La répartition des charges horizontales sur les éléments de contreventement doit être déterminée en utilisant le système de contreventement de la Figure 01.

Épaisseur de paroi t = 30 cm

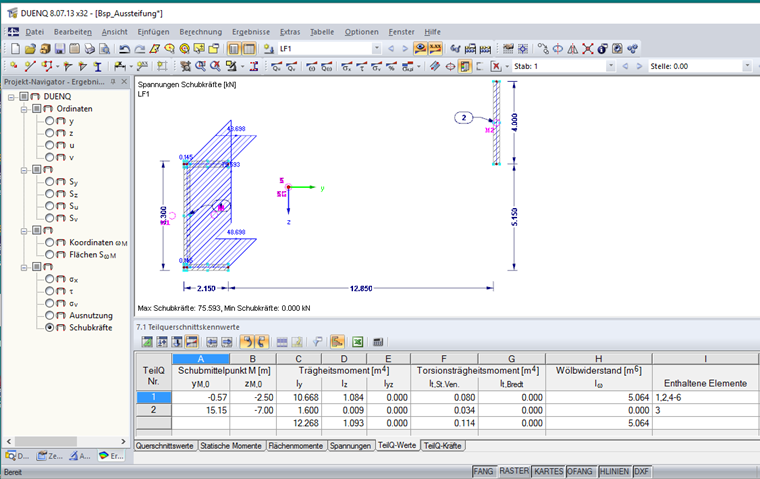
Propriétés des sections

Section partielle 1

Section partielle 2

Section brute
I_y = 10,668 + 1,600 = 12,268 m⁴
I_z = 1,084 + 0,009 = 1,093 m⁴

Les propriétés de la section déterminées dans SHAPE-THIN 8 sont affichées sur la Figure 02.

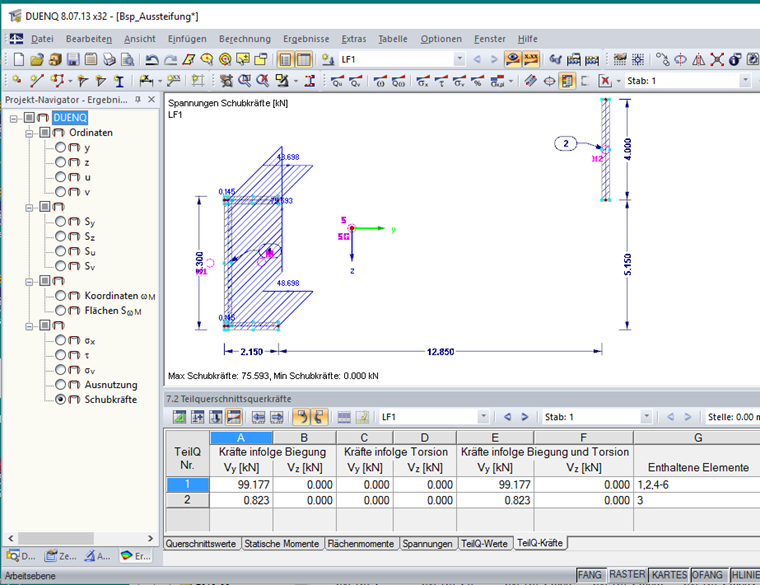
Efforts de section de paroi de cisaillement

Les efforts tranchants de la section partielle déterminés dans SHAPE-THIN 8 sont représentés sur la Figure 03.

Références

[1] Beck, H.; Schäfer, H.: Die Berechnung von Hochhäusern durch Zusammenfassung aller aussteifenden Bauteile zu einem Balken. Der Bauingenieur, livre 3, 1969